基于https://www.bilibili.com/video/BV164411m79z?p=24?观后笔记
相关函数定义介绍
代价/成本函数和损失函数
损失函数(Loss/error function)是定义在单个训练样本上的，即一个样本的误差。
代价函数(Cost function)是定义在整个训练集上面的，对所有样本的误差的总和求平均值。
但由于实质相同，都是事先定义一个假设函数，通过训练集由算法找出一个最优拟合，即使得函数值最小(如通过梯度下降法)，从而估计出假设函数的参数。所以往往我所看到的大多将代价函数和损失函数视为同一东西，下文就不给予区分，以损失函数来讲。（求和除以样本数的为代价函数，否则为损失函数）
损失函数
损失函数（loss function）是用来估量模型的预测值f(x)与真实值Y的不一致程度，即度量拟合程度。它是一个非负实值函数，通常使用 L(Y, f(X)) 来表示，损失函数越小，模型的拟合越好，鲁棒性越好。
但是并不是损失函数越小，结果就越好。
如何理解整个分类过程
1.首先从初中学习的线性回归来看（下图）
给出了一系列数据（红点），我们要做的就是找到一条合适直线来拟合这些数据的分布，本质上来说就是找到满意的参数
2.而逻辑回归也是如此，只不过初中是直接简单粗暴的通过公式的出了这么一条直线，而现在是要不断试错，不断改进地找出满意的参数
首先我们也假设训练集符合 z（x） 这个函数，通过输出x可以得到”预测值“z。
请注意，我们希望的是预测值可以告诉我们”该分到哪一类“，比如有一张图片，我们希望通过输入图片的RGB，得到的是这张图可不可以判断它上面是猫的概率
而概率只有0~1才有意义，因此最后的输出结果应该只能有0~1，然后这里显然z的值是我们难以预料了，可能很大，甚至可能是负值。因此，我们引入sigmoid函数
?
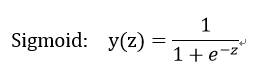
这样就把结果限制在0~1了，下面称y_hat / y帽 / y^ 为新预测值（下文直接称为预测值）
这个y_hat就是我们希望得到的结果（即已知x|y=1的概率)，更具体的说，也是正向传播中的一个产物。至此sigmoid(z)就是我们的预测函数
重点来了：
? ? ? ? 我们要怎么定义预测函数的好坏呢? ————损失函数(Loss Function)，顾名思义，我们肯定是要所谓的损失（代表的是预测值和实际值的误差）越小越好
不过在继续之前，先来讲讲怎么找到这个损失函数
通过y_hat的定义，我们可得出：
这确实就是一个离散型的概率函数
进一步得到这个概率函数的最终表达式：
（别问怎么推导的，问就是大佬牛逼）
不过我们还是验证这个公式的正确性的，但是视频里有讲解（P24），这里就不赘述了。
又根据概率论中最大概率原理：发生了的就是概率最大的
所以，我们要让P(y|x)最大，因为在训练过程中，y是知道的。（其实就是想成概率论中用极大似然估计求参数这类题，y是观测值之一。）
怎么取最大呢？用回解题的套路，先给它整个log（也是因为log单调函数，不会影响找P(y|x)最大值，log(P(y|x)),? P(y|x)也最大）然后我们就可以得到：
并让它最大化
这时候，再回想起我们的损失函数，我们要使损失最小化，这不就和这个函数的要求相反了吗？那我们在这个log函数的基础上添个负号不就弄出损失函数了？
从而定义损失函数
?要注意的是损失函数是针对单个样本的，而对应整个训练集，我们引入成本函数(Cost Function)。
这里要回想起概率论中的极大似然估计，这一整组训练集已经”发生“，根据极大似然估计，此情况发生的概率要是最大的！ 所以有下列推导
同样的，我们要最大化这个求和，而总体的成本函数要最小化，所以定义成本函数为
去掉了负号，同时加了个1/m的因子，个人理解是将总成本分摊到每个训练集，由此获得比单个训练集的损失函数值更具代表性的值
?至此，其实就完成了正向传播的准备，要做的就是像视频那样用numpy模块&矩阵运算的知识把for循环去掉，进行算法上的优化。
反向传播也可以从视频了解到过程。
?
?
?
?
?
?
?
?
?
?
?
?
?