一、逻辑回归

? 对于二元分类问题来讲，给定一个输入特征向量𝑋，它可能对应一张图片，若想识别这张图片识别看它是否是一只猫或者不是一只猫的图片，想要一个算法能够输出预测，称之为𝑦^，也就是对实际值 𝑦 的估计。更正式地来说，要想让 𝑦^ 表示 𝑦 等于 1 的一种可能性或者是机会，前提条件是给定了输入特征𝑋。换句话来说，如果𝑋是我们在上个视频看到的图片，想让 𝑦^ 来告诉你这是一只猫的图片的机率有多大。在之前的视频中所说的，𝑋是一个𝑛𝑥维的向量（相当于有𝑛𝑥个特征的特征向量）。我们用𝑤来表示逻辑回归的参数，这也是一个𝑛𝑥维向量（因为𝑤实际上是特征权重，维度与特征向量相同），参数里面还有𝑏，这是一个实数（表示偏差）。所以给出输入𝑥以及参数𝑤和𝑏之后，我们怎样产生输出预测值𝑦^，一件你可以尝试却不可行的事是让𝑦^ =? $w^{t}x+b$

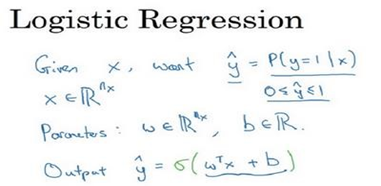
? ?下面是关于𝑧的 sigmoid 函数的图像。我们通常都使用𝑧来表示𝑤𝑇𝑥 + 𝑏的值：

二、逻辑回归的代价函数

1.损失函数：损失函数又叫做误差函数，用来衡量算法的运行情况，Loss function:𝐿(𝑦^ , 𝑦).

? 我们通过这个𝐿称为的损失函数，来衡量预测输出值和实际值有多接近。一般我们用预测值和实际值的平方差或者它们平方差的一半，但是通常在逻辑回归中我们不这么做，因为当我们在学习逻辑回归参数的时候，会发现我们的优化目标不是凸优化，只能找到多个局部最优值，梯度下降法很可能找不到全局最优值，虽然平方差是一个不错的损失函数，但是我们在逻辑回归模型中会定义另外一个损失函数。

2.梯度下降法

如图，在第二行给出和之前一样的逻辑回归算法的代价函数（成本函数）梯度下降法的形象化说明。

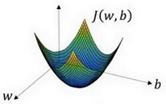
?在这个图中，横轴表示你的空间参数𝑤和𝑏，在实践中，𝑤可以是更高的维度，但是为了更好地绘图，我们定义𝑤和𝑏，都是单一实数，代价函数（成本函数）𝐽(𝑤, 𝑏)是在水平轴𝑤和 𝑏上的曲面，因此曲面的高度就是𝐽(𝑤, 𝑏)在某一点的函数值。我们所做的就是找到使得代价函数（成本函数）𝐽(𝑤, 𝑏)函数值是最小值，对应的参数𝑤和𝑏。

?如图，代价函数（成本函数）𝐽(𝑤, 𝑏)是一个凸函数(convex function)，像一个大碗一样?。

?如图，这就与刚才的图有些相反，因为它是非凸的并且有很多不同的局部最小值。由于逻辑回归的代价函数（成本函数）𝐽(𝑤, 𝑏)特性，我们必须定义代价函数（成本函数）𝐽(𝑤, 𝑏) 为凸函数。初始化𝑤和𝑏。

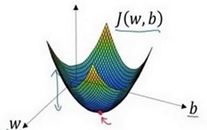
?可以用如图那个小红点来初始化参数𝑤和𝑏，也可以采用随机初始化的方法，对于逻辑回归几乎所有的初始化方法都有效，因为函数是凸函数，无论在哪里初始化，应该达到同一点或大致相同的点。

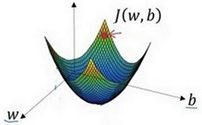
?我们以如图的小红点的坐标来初始化参数𝑤和𝑏。

三、m 个样本的梯度下降

在之前的视频中,已经看到如何计算导数，以及应用梯度下降在逻辑回归的一个训练样本上。现在我们想要把它应用在𝑚个训练样本上。

当我们的算法输出关于样本𝑦的 $a^{(i)}$ , $a^{(i)}$ 是训练样本的预测值，即：𝜎( $z^{(i))}$ ?) = 𝜎( $w^{t}x^{(i))}$ ?+ 𝑏)。所以我们在前面的幻灯中展示的是对于任意单个训练样本，如何计算微分当你只有一个训练样本。因此𝑑𝑤1，𝑑𝑤2和𝑑𝑏 添上上标𝑖表示你求得的相应的值。如果面对的是我们在之前的幻灯中演示的那种情况，但只使用了一个训练样本( $x^{(i)}$ ?, $y^{(i)}$ ?)。