[人工智能]pytorch深度学习实践_p4_Backpropagation

对于Backpropagation的一些理解

做gradient descent 的关键步骤是求loss对w（特征值，这里就用weight做示例）求导，当没有用到神经网络的时候对于其还是比较好求的，但是当嵌套了多层神经元后，其求导难度就大大增加了。这时backpropagation的作用就来了通过一次forward和一次backward以后就能求出。过程如下：

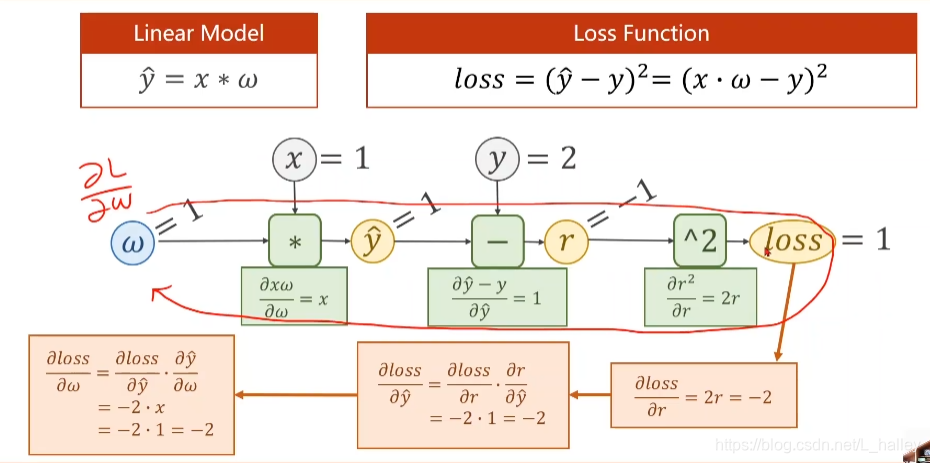
总结 ：backpropagation的作用就是在神经网络中求出最后一层一层对于第一层input的导数，以便进行梯度下降

torch

• w.required_grad()

作用告诉Tensor需要计算梯度，默认不需要

• item（）与data（）的区别

• item()返回的是一个具体的数值。
  注意：对于元素不止一个的tensor列表，使用item()会报错
• .data返回原数据的深度拷贝是一个无梯度的tensor，=，即不会生成计算图

作业代码

这里的训练感觉有点问题，我预想的函数是y = x^2 + 2*x + 1，w2的初始值如果不是给的2的话预测偏差会特别大，但是w2的初始值不应该只是会影响梯度下降的速度吗？最终应该都会下降到2左右呀，不应该导致最终预测结果出现特别大的误差

import numpy as np
import matplotlib.pyplot as plt
import torch
x_data = [1.0, 2.0, 3.0, 4.0]
y_data = [4.0, 9.0, 16.0, 25.0]

w1 = torch.Tensor([1.0])  #将w变成张量，可以认为是一个高维数组
w1.requires_grad = True   #需要计算梯度
w2 = torch.Tensor([2.0])
w2.requires_grad = True
b = torch.Tensor([1.0])
b.requires_grad = True
def forward(x):
    return w1*x**2 + w2*x +b

def loss(x,y):
    y_pre = forward(x)
    return (y_pre-y)**2

print("Predict (before training)",4,forward(4).item()) #这里因为w是张量，所以w*x后，返回的也是个张量，所以需要item（）取值

for epoch in range(100):
    for x, y in zip(x_data, y_data):
        l = loss(x, y)
        l.backward()
        print("\tgrad: ", x, y, w1.grad.item(), w2.grad.item(), b.grad.item())
        w1.data = w1.data - 0.01*w1.grad.data
        w2.data = w2.data - 0.01 * w2.grad.data
        b.data = b.data - 0.01 * b.grad.data

        w1.grad.data.zero_()  #这里需要把这个计算图中求得数据清0 防止对下一个循环的值产生影响，当然这个不是所有的都要清零，有一些案例需要用到前一计算图的结果
        w2.grad.data.zero_()
        b.grad.data.zero_()
    print("progress: ", epoch, l.item())
print("Predict (before training)",4,forward(4).item())