《PyTorch深度学习实践》学习笔记【2】

学习资源：
《PyTorch深度学习实践》完结合集

二、线性模型

2.1 概念：

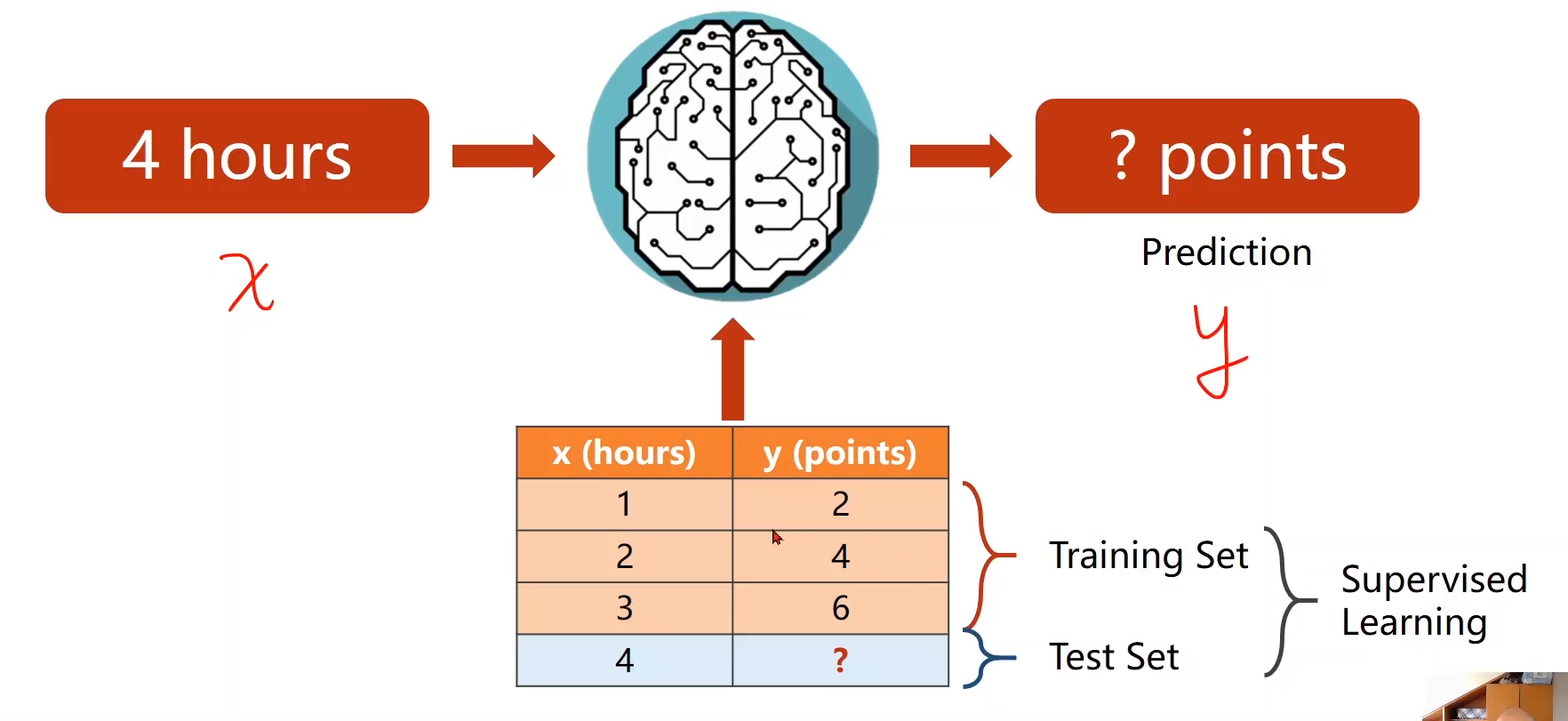
2.1.1 数据集和测试集

? 数据集拿到后一般划分为两部分，训练集和测试集，然后使用训练集的数据来训练模型，用测试集上的误差作为最终模型在应对现实场景中的泛化误差。

? 一般来说，测试集在训练的时候是不能偷看的。

我们可以使用训练集的数据来训练模型，然后用测试集上的误差作为最终模型在应对现实场景中的泛化误差。有了测试集，我们想要验证模型的最终效果，只需将训练好的模型在测试集上计算误差，即可认为此误差即为泛化误差的近似，我们只需让我们训练好的模型在测试集上的误差最小即可。

? 为了使得模型在现实生活中更有效，我们要使用的数据集要尽可能真实。

2.1.2 过拟合与泛化

下面拿小猫图像识别做例子，说明一下过拟合和泛化的概念；

过拟合：在训练集上匹配度很好，但是太过了，把噪声什么的也学进来了。

泛化能力：对于没见过的图像也能进行识别，这是我们所需要的。

2.1.3 开发集

有时候无法看到测试集，我们又人为地把数据集划分一部分出来作为验证评估，称为“开发集”。

2.1.4 监督学习和非监督学习

有监督学习方法必须要有训练集与测试样本。在训练集中找规律，而对测试样本使用这种规律。而非监督学习没有训练集，只有一组数据，在该组数据集内寻找规律。

有监督学习的方法就是识别事物，识别的结果表现在给待识别数据加上了标签。因此训练样本集必须由带标签的样本组成。而非监督学习方法只有要分析的数据集的本身，预先没有什么标签。如果发现数据集呈现某种聚集性，则可按自然的聚集性分类，但不予以某种预先分类标签对上号为目的。

2.2 线性回归

2.2.1 线性模型

如 y= kx+b ，我们训练的结果就是k和b的值

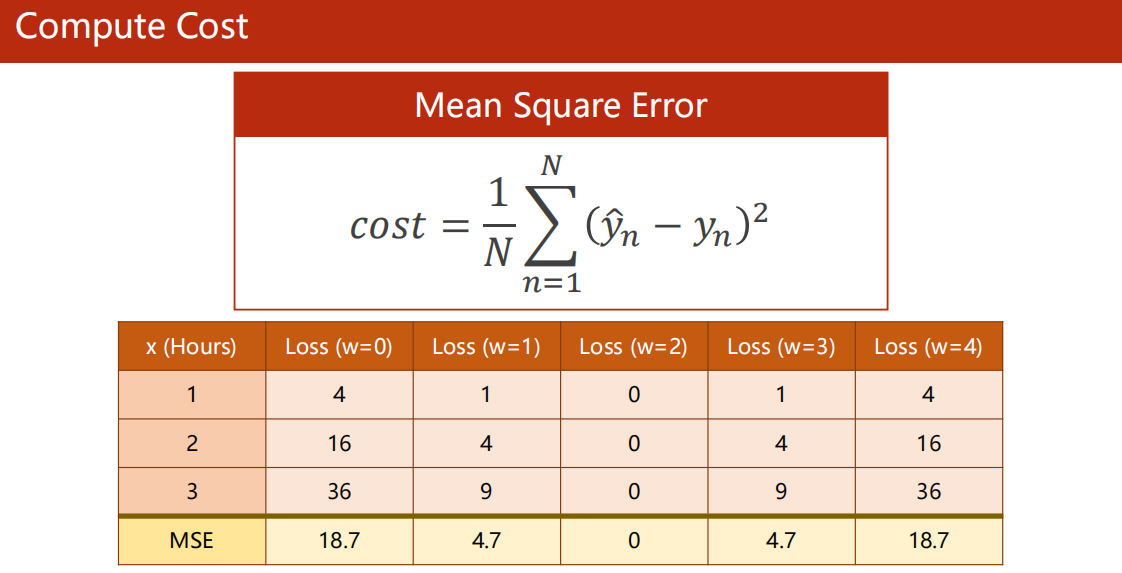
2.2.2 损失函数

误差函数

平均平方误差（MSE）

损失函数的值越小，代表拟合的效果越好。

2.3 课上实验【1】

课上代码：

import numpy as np
import matplotlib.pyplot as plt;
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

#线性模型
def forward(x):
    return x * w

#损失函数
def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) * (y_pred - y)

#迭代取值，计算每个w取值下的x，y，y_pred,loss_val
w_list = []
mse_list = []
for w in np.arange(0.0, 4.1, 0.1):
    print('w=', w)
    l_sum = 0
    for x_val, y_val in zip(x_data, y_data):
        y_pred_val = forward(x_val)
        loss_val = loss(x_val, y_val)
        l_sum += loss_val
        print('\t', x_val, y_val, y_pred_val, loss_val)
    print('MSE=', l_sum / 3)
    w_list.append(w)
    mse_list.append(l_sum / 3)

##画图
plt.plot(w_list, mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()

结果：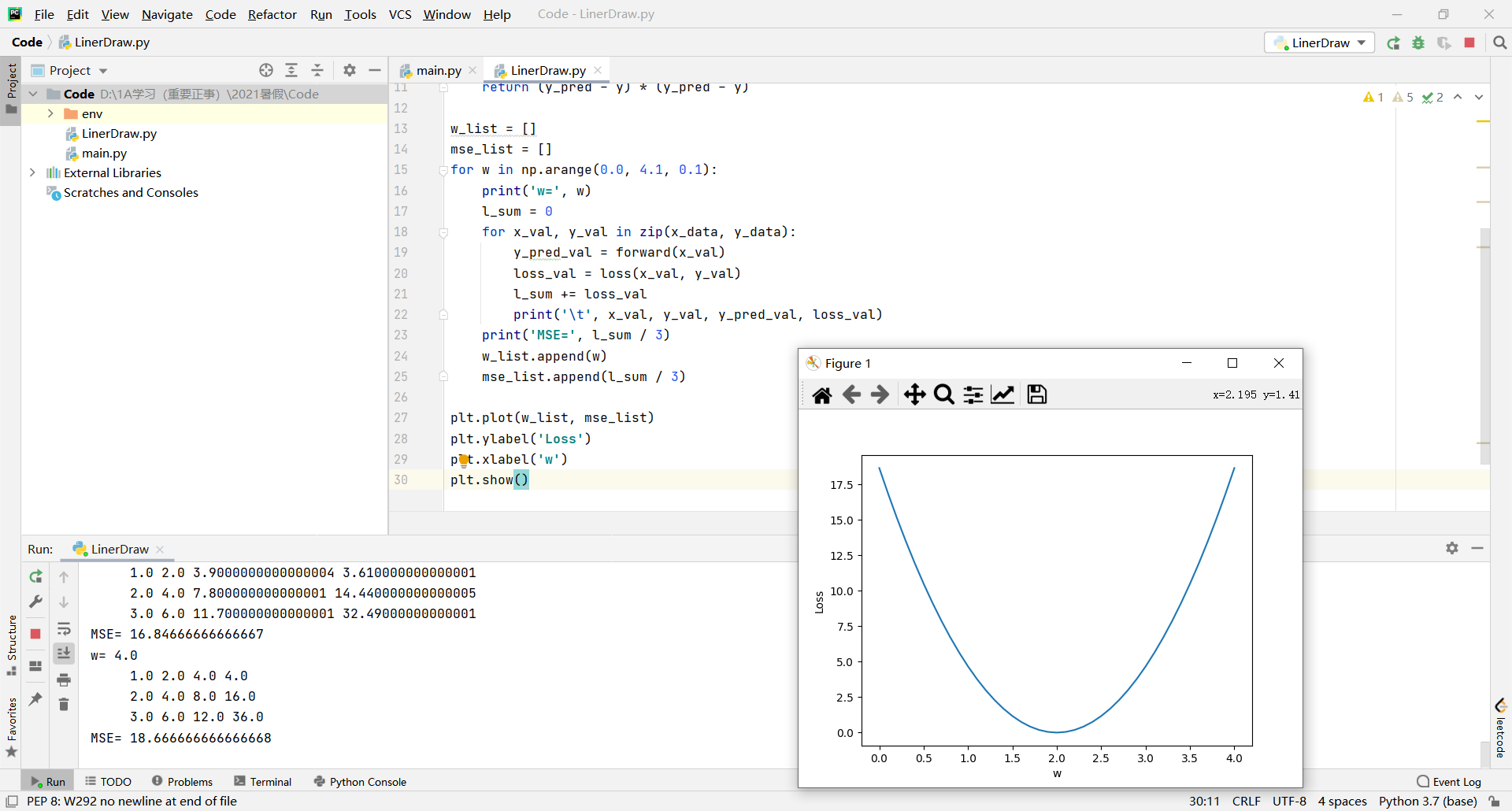

2.4 作业【1】：

参考 Matplotlib3D作图-plot_surface(), .contourf(), plt.colorbar()

代码：

import numpy as np
import matplotlib.pyplot as plt;
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

#线性模型
def forward(x,w,b):
    return x * w+ b

#损失函数
def loss(x, y,w,b):
    y_pred = forward(x,w,b)
    return (y_pred - y) * (y_pred - y)


def mse(w,b):
    l_sum = 0
    for x_val, y_val in zip(x_data, y_data):
        y_pred_val = forward(x_val,w,b)
        loss_val = loss(x_val, y_val,w,b)
        l_sum += loss_val
        print('\t', x_val, y_val, y_pred_val, loss_val)
    print('MSE=', l_sum / 3)
    return  l_sum/3

#迭代取值，计算每个w取值下的x，y，y_pred,loss_val
mse_list = []



##画图

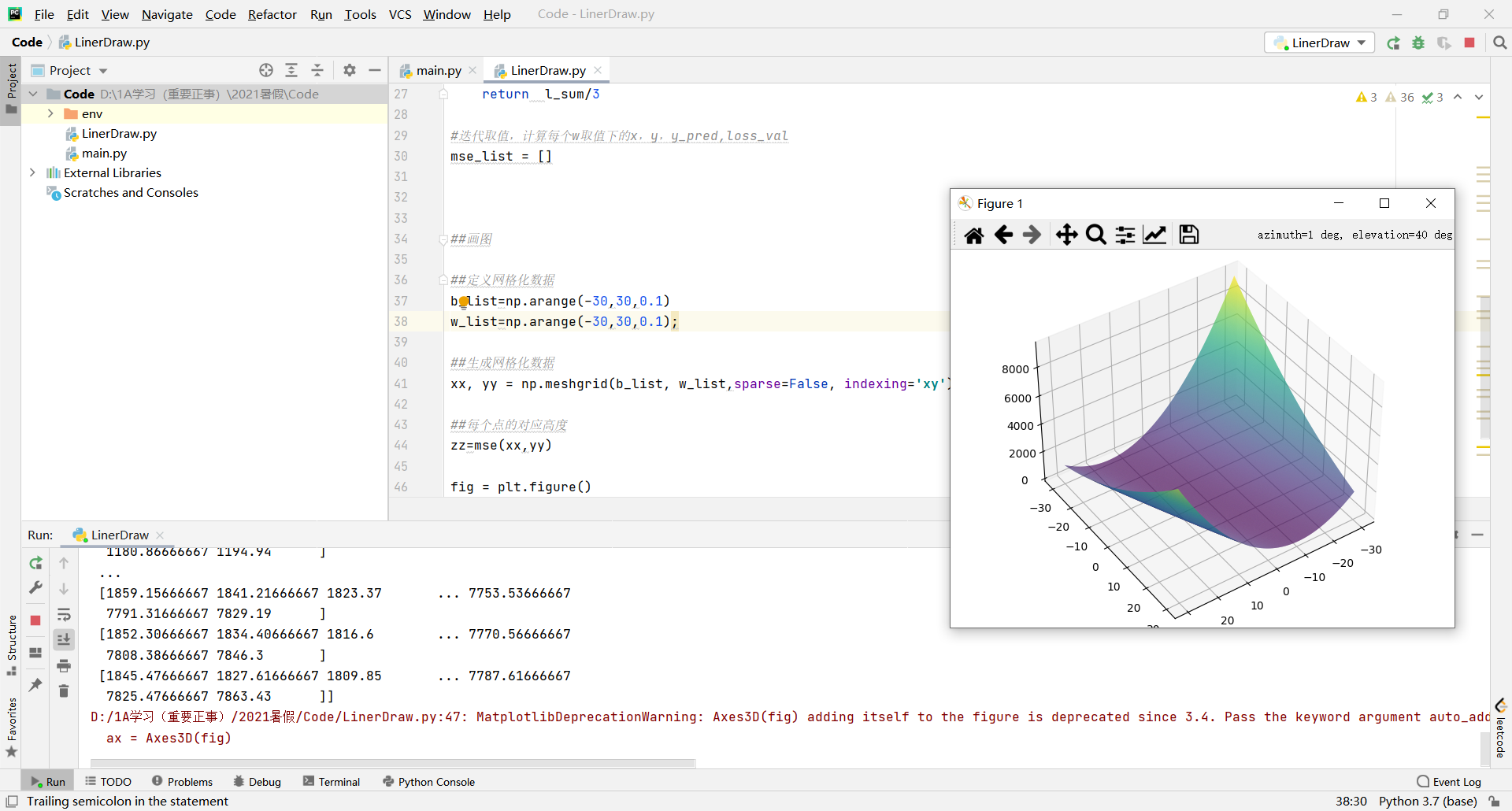
##定义网格化数据
b_list=np.arange(-30,30,0.1)
w_list=np.arange(-30,30,0.1);

##生成网格化数据
xx, yy = np.meshgrid(b_list, w_list,sparse=False, indexing='xy')

##每个点的对应高度
zz=mse(xx,yy)

fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(xx, yy, zz, rstride=1, cstride=1, cmap=cm.viridis)
plt.show()