[人工智能]CS224W图机器学习笔记12-motif和子图

图神经网络

课程和PPT主页

Subgraphs and Motifs

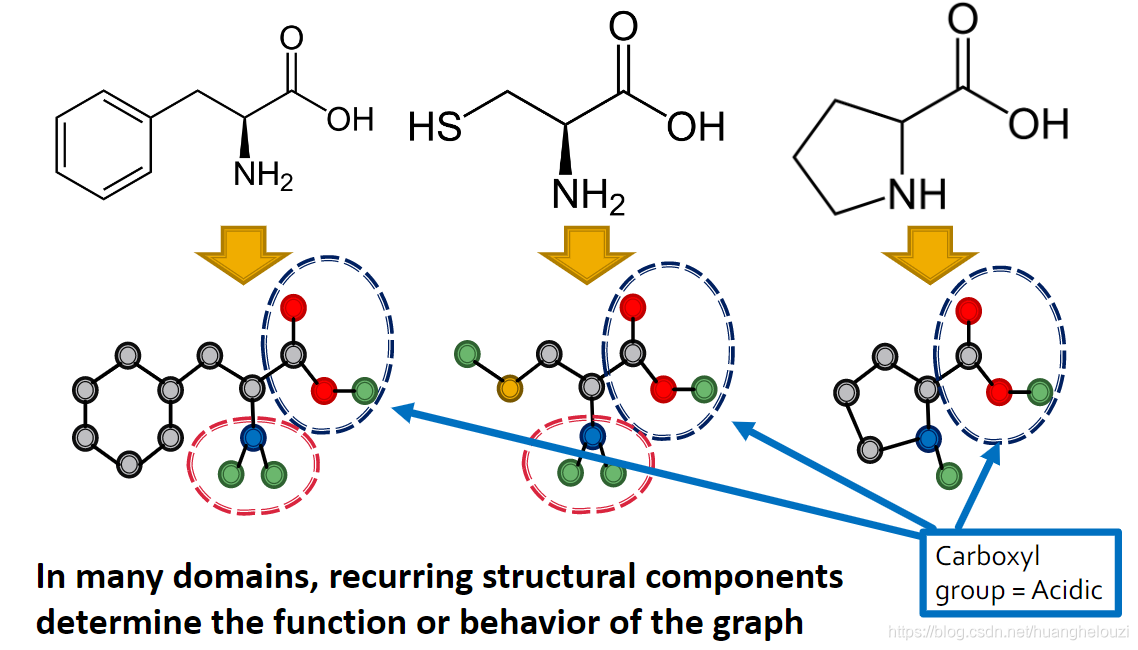
子图（Subgraphs）是图的一部分，可理解子图为积木（building blocks），由子图构建出整个图。在很多领域，很多重复出现的的子图决定了整图的功能。下面给出一个生物网络中的例子，若图中出现Carboxyl这个子图结构，那么整个蛋白质将会有酸味这个性质。

有两种方式可以形式化的定义子图：Node-induced subgraph，Edge-induced subgraph(不常使用)。


在不同的领域和不同的场景下使用不同的子图定义方法，一般情况下，使用Node-induced subgraph比较多，因为Edge-induced subgraph的时间复杂性比较大。

当然子图可以来自其他完整的图，这时候就变成了某个子图是否包含在图中的问题。

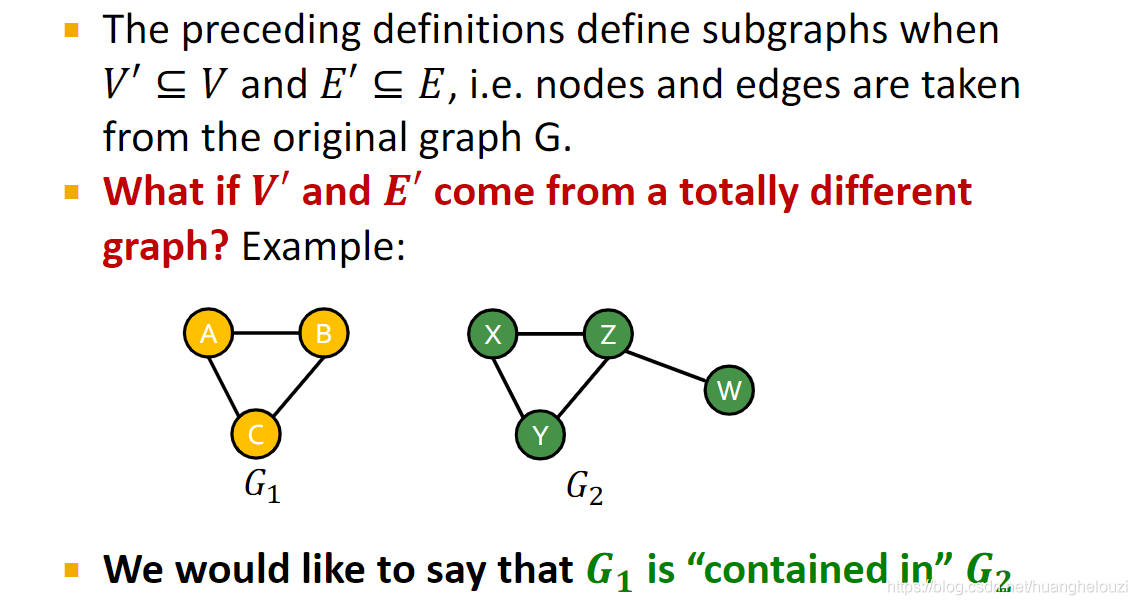
图同构问题（Graph isomorphism problem）：注意同构和相同是存在区分的，主要是因为图中节点无需考虑顺序问题（如节点a的邻居节点有bcd和节点a的邻居节点有cbd是一样的）。

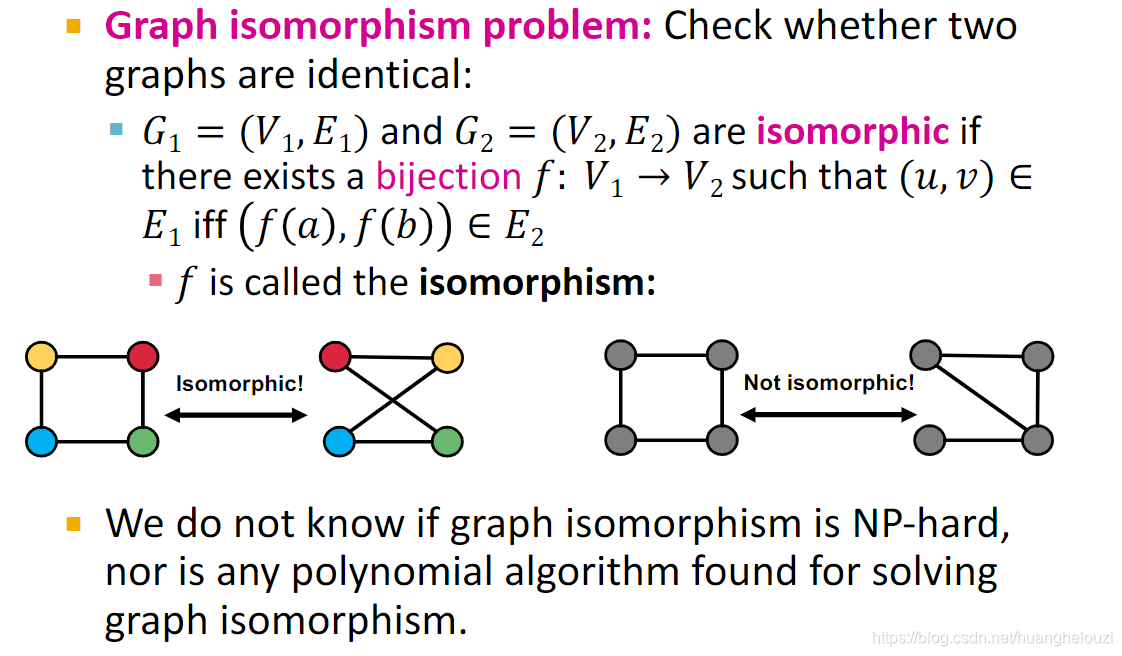
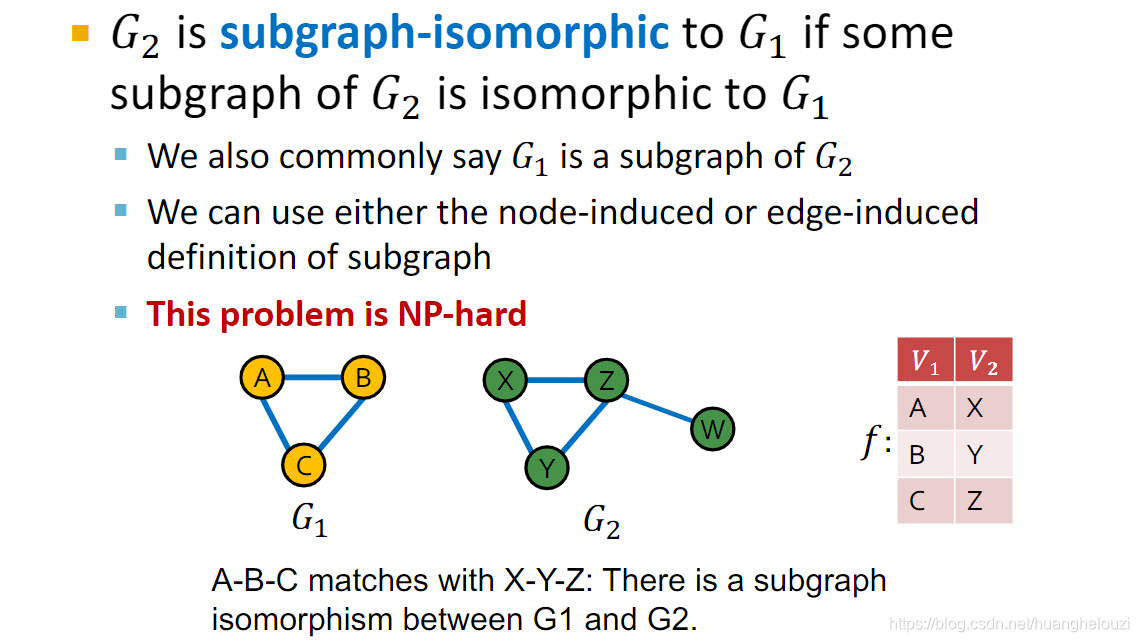
由图同构问题，我们可以得到子图同构问题，该问题换句话说就是某个图是否包含在另一个图中。比如下面图$G_1$和$G_2$的子图(xyz)同构，也就是说$G_1$包含在$G_2$中。

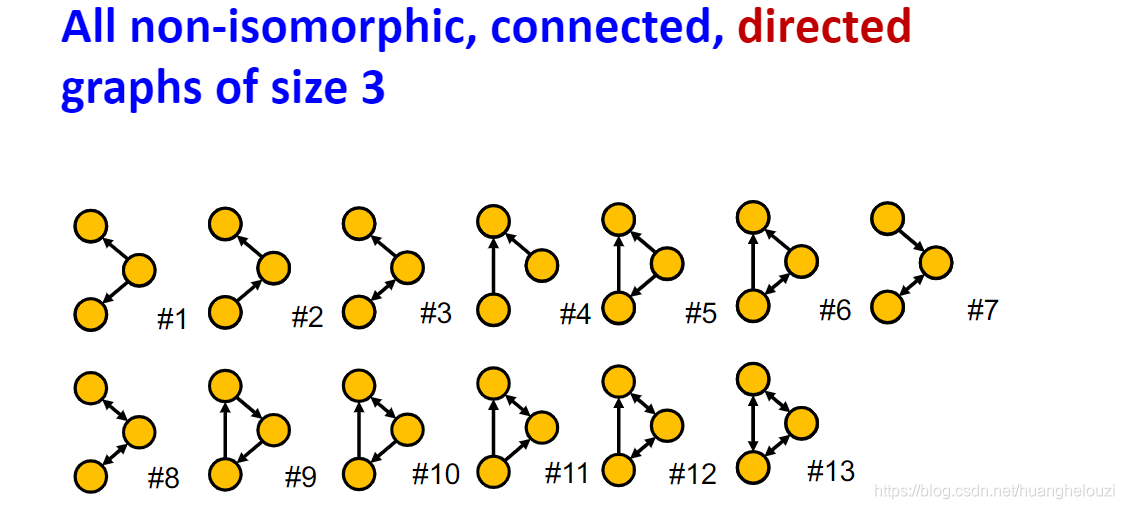
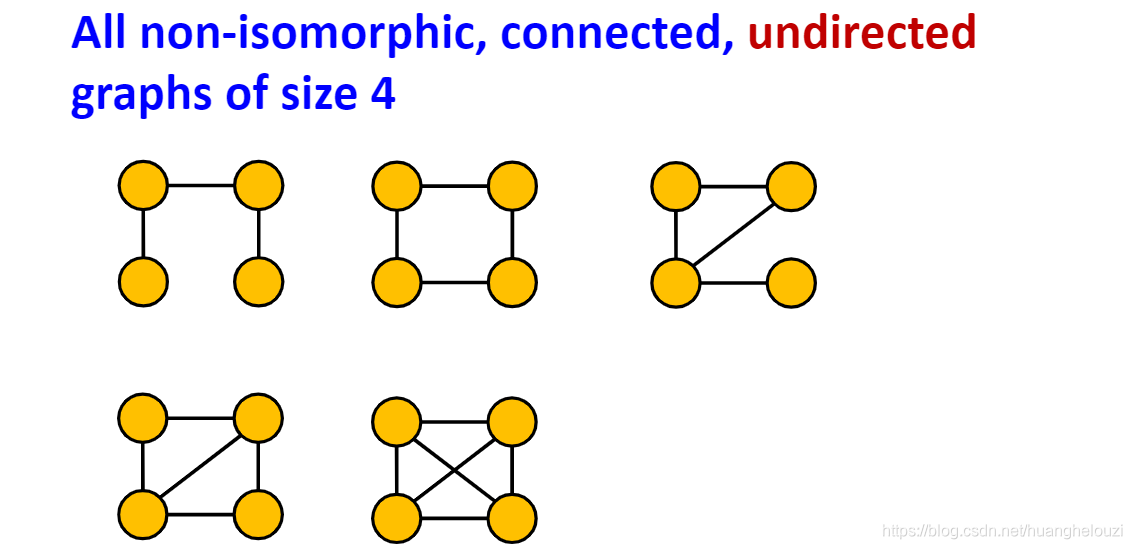
给定节点数量，我们可获得很多个非同构的、连通的、边数量不定的子图。其中在某些出现频率高的、比较重要的一部分子图被称为motifs。下面给出节点数量为3和4时的所有非同构的、连通的、边数量不定的子图，当给定节点数量比较大时，这种子图数量将快速增长。


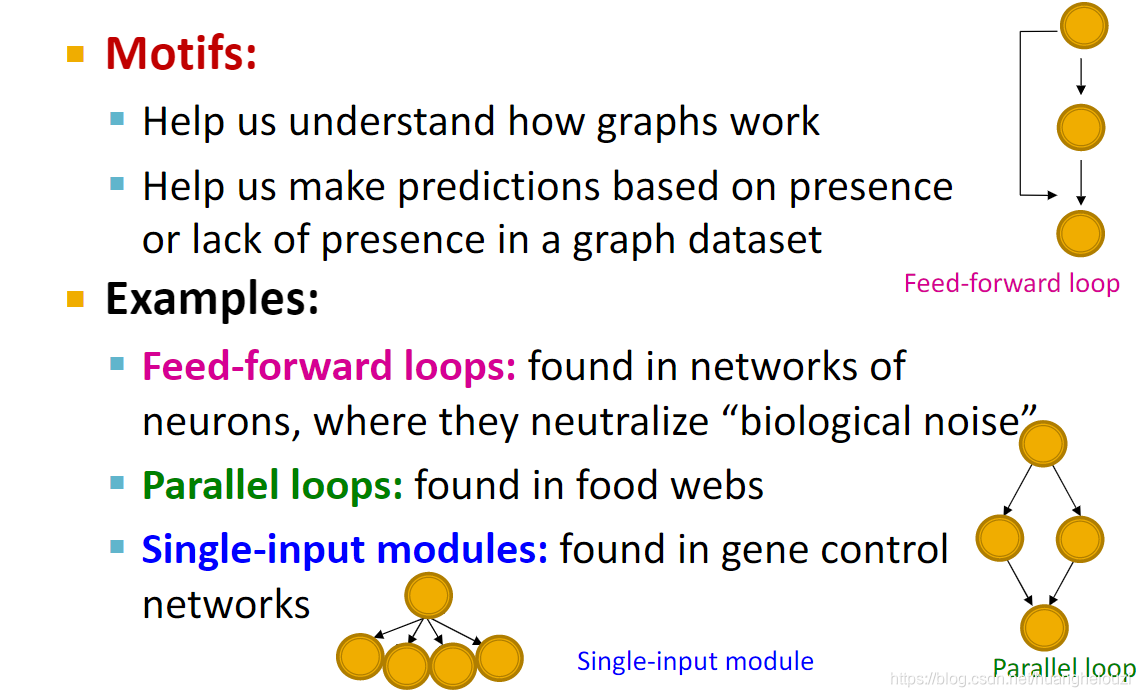
下面给出motifs的定义和例子，motifs的特征是多次出现的、重要的小的子图。

那么motifs有什么用呢？下图将会给出motifs的作用和常见的motifs例子。

上面说到motifs的特征是多次出现的、重要的小的子图。所以有两个指标需要衡量，一是频率(Frequency)，二是重要性(significance)。

频率分为两种：Graph-level Subgraph Frequency和Node-level Subgraph Frequency。


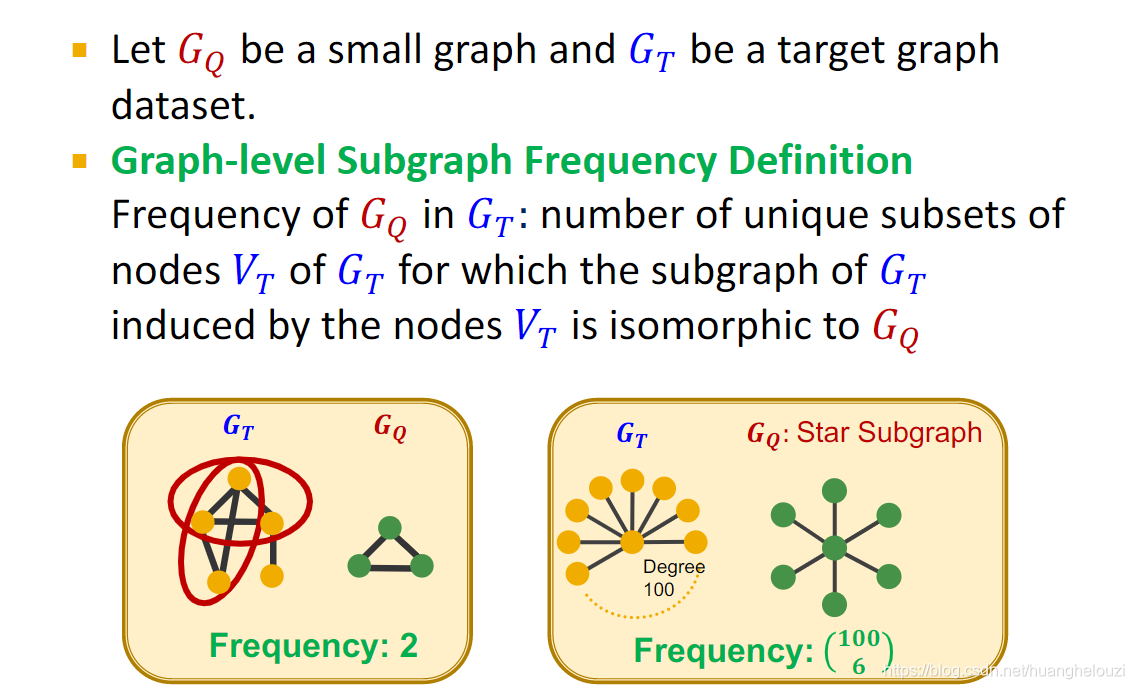
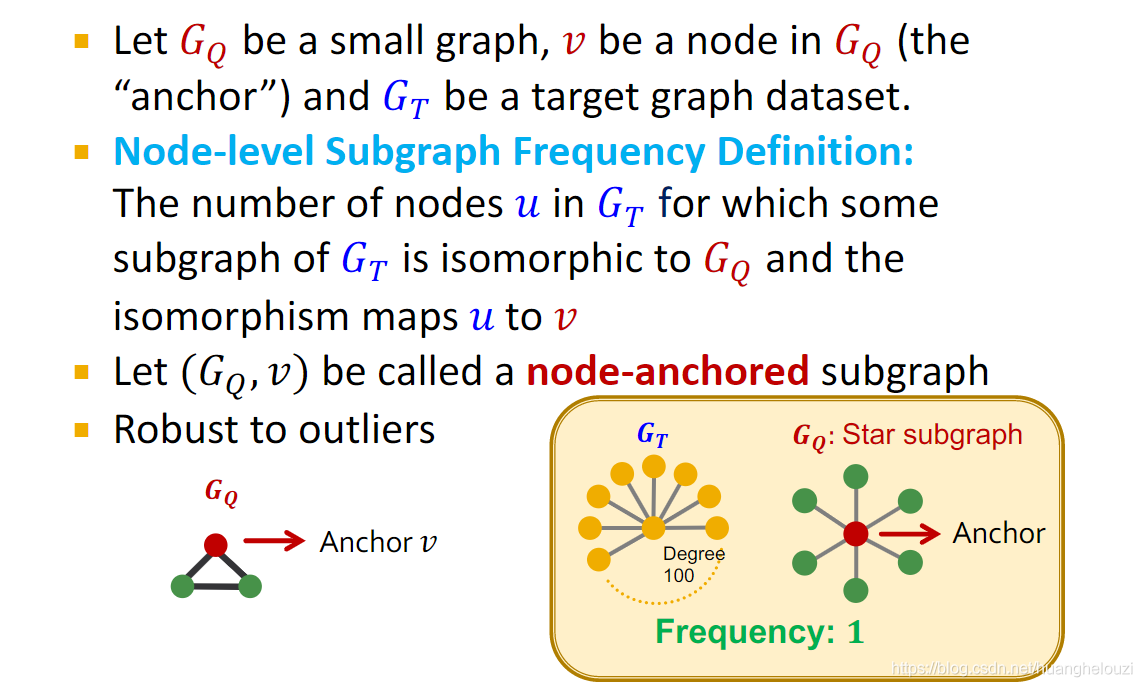
特殊地，这两个频率定义可以扩展到非连通图，只需要把每个连通分量视为一个独立的图即可。

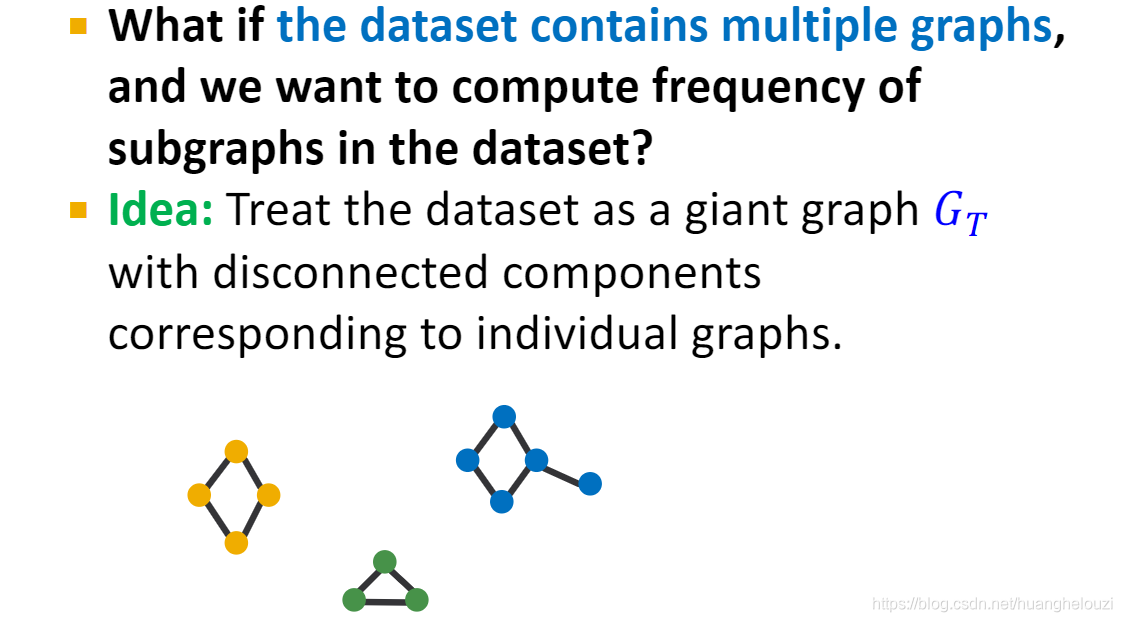
而子图重要性(significance)的定义就比较复杂，首先需要定义一个null-model（也就是一个随机图），若一个子图出现在真实图（与之对应的就是随机图）的次数比出现在随机图中的次数越多，该子图的重要性就越大。

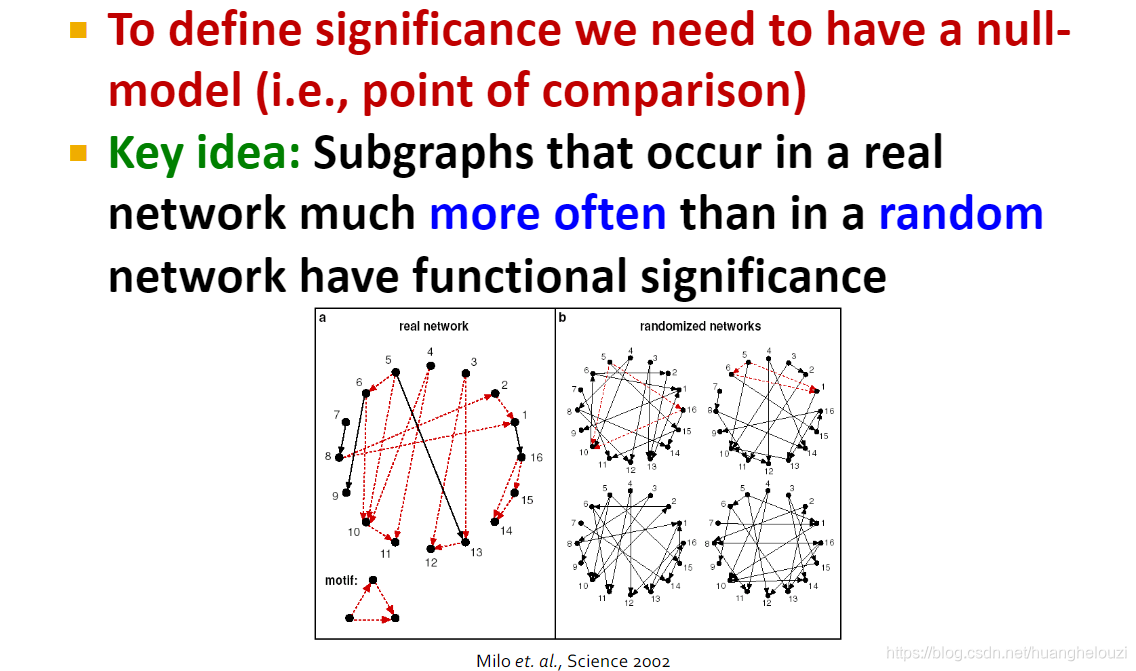
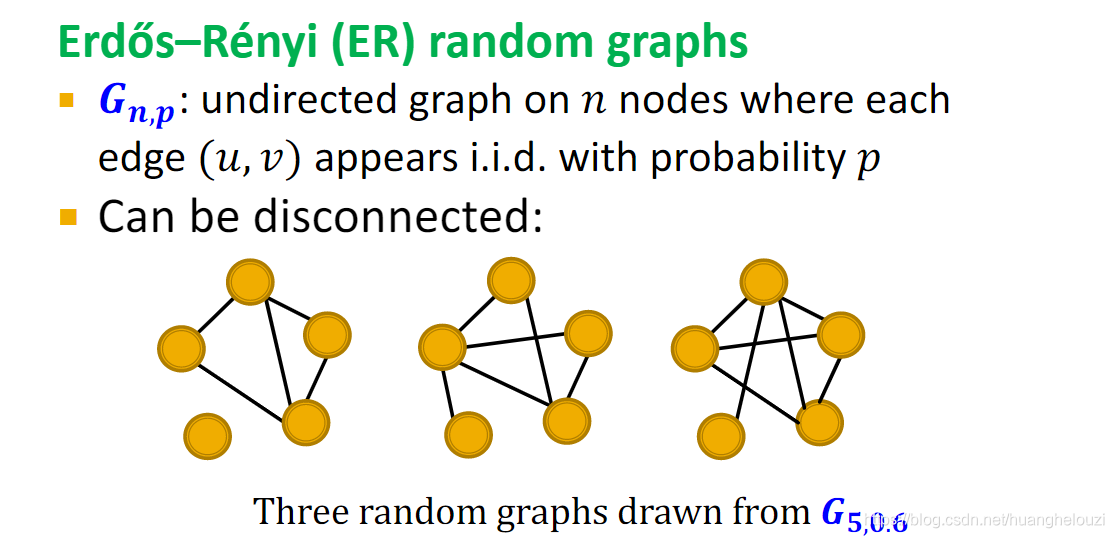
那么如何快速的生成随机图，用以后继任务的比较呢？随机图生成模型主要有两种：Erd?s–Rényi (ER) random graphs和Configuration model。
Erd?s–Rényi (ER) random graphs比较简单，首先生成n个节点，然后两两节点之间以概率p生成边。

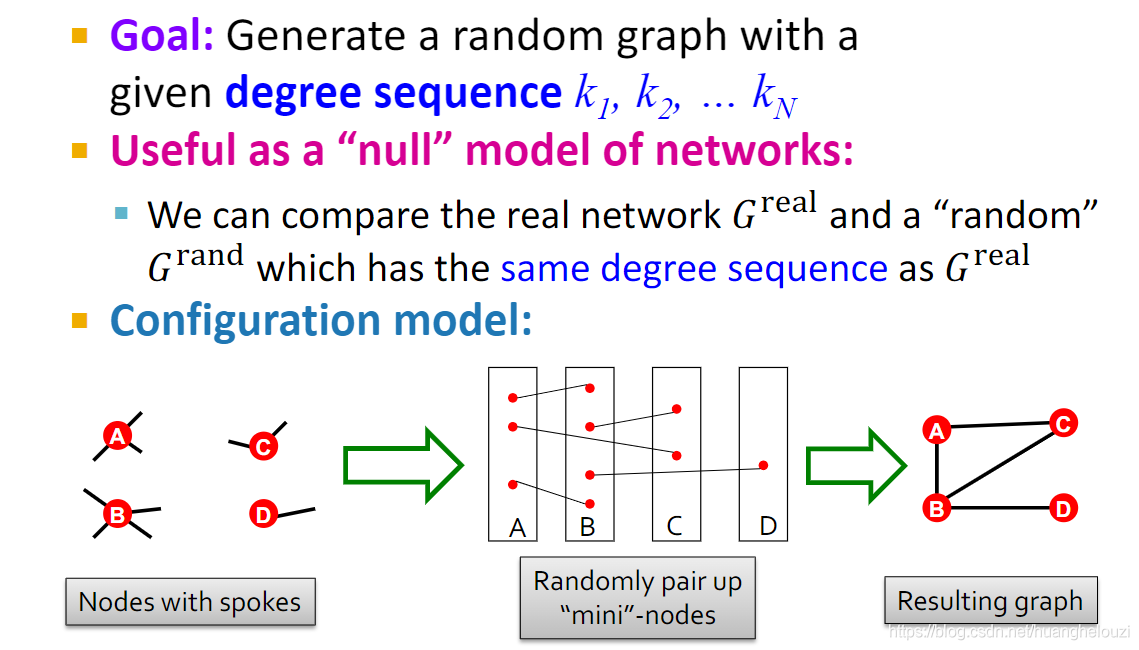
Configuration model比较复杂，需要给定节点数量n之外，还需要给定节点的度数。需要注意的是：节点生成边的过程中，可能会出现重复边和自循环边，可忽略这两种类型边，因为这两类边出现概率很低。

Motif重要性计算过程如下：



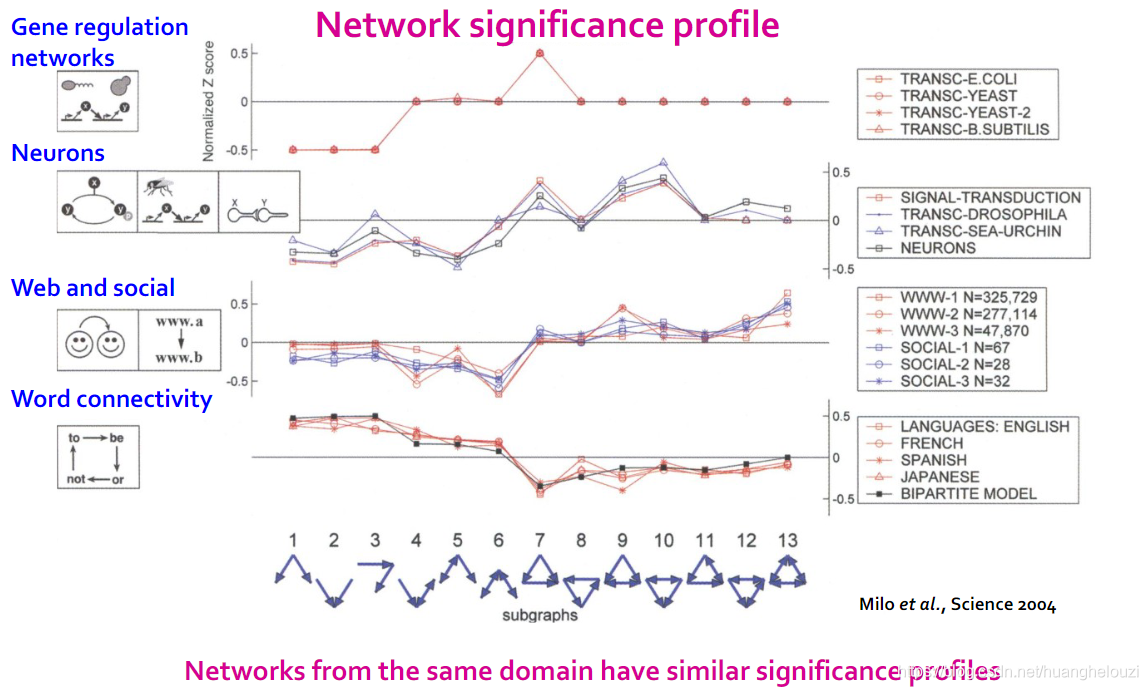
下面给出significance profile重要性的例子，纵轴为SP（significance profile，也就是归一化的Z Score）值，横轴为13个节点数量为3的子图，我们以下的发现：

• 来自同一领域的网络具有相似的significance profiles
• significance profiles值大小与我们正常认知相同。比如在社交网络中，我有两个朋友，那么这个两个朋友之间应该很大概率也是朋友关系，故在第三行里子图6的SP值很小子图13的SP值很大，这说明子图13在社交网络图中很重要，即子图13是社交网络的motif。
  
  来总结一下motif的计算过程，需要注意的步骤2中是使用多个随机图进行计算的；步骤3中计算子图重要性方法还可使用归一化的Z-score等。
  
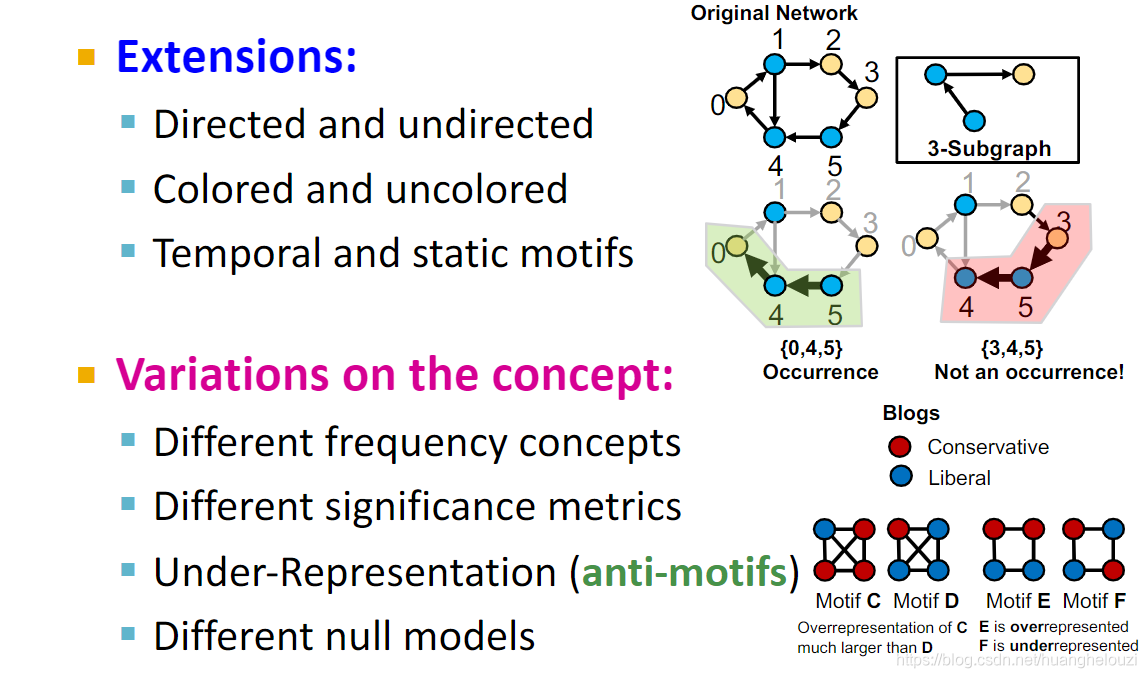
  同样motif概念还可以扩展到其他不同的图中
  
  总结：
  

Neural Subgraph Matching

子图匹配问题描述：一个较小的子图是否是一个大图的子图。在下面的例子中，查询图是图的子图，图中相同颜色节点是一一映射关系。

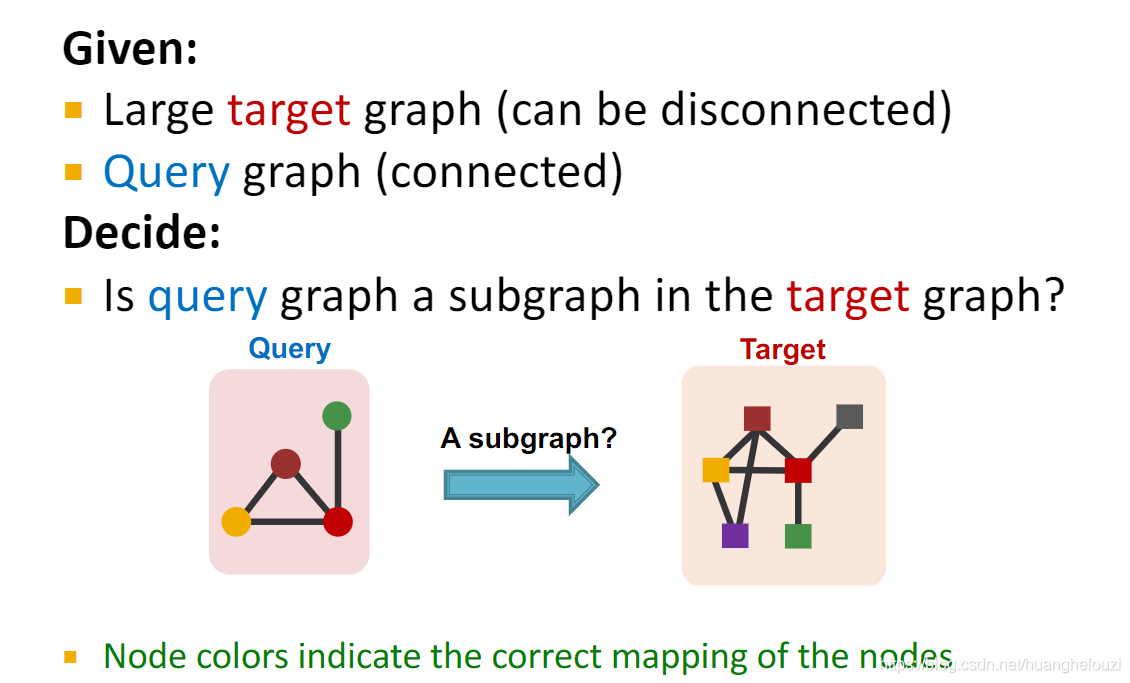
同时这个子图匹配问题可以使用GNN实现，使用的是节点嵌入进行比较。而非GNN方法通常需要逐节点逐边进行比较。

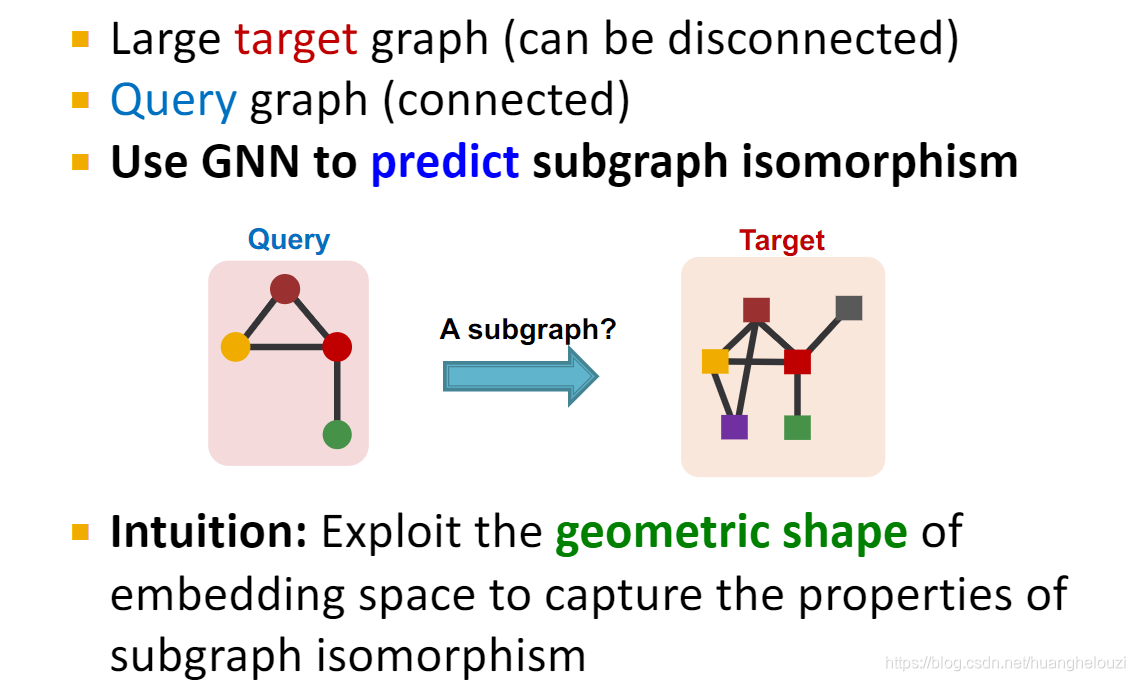
而GNN子图匹配通常考虑的是：子图是否包含在图中，而不关注子图在图中的什么位置。

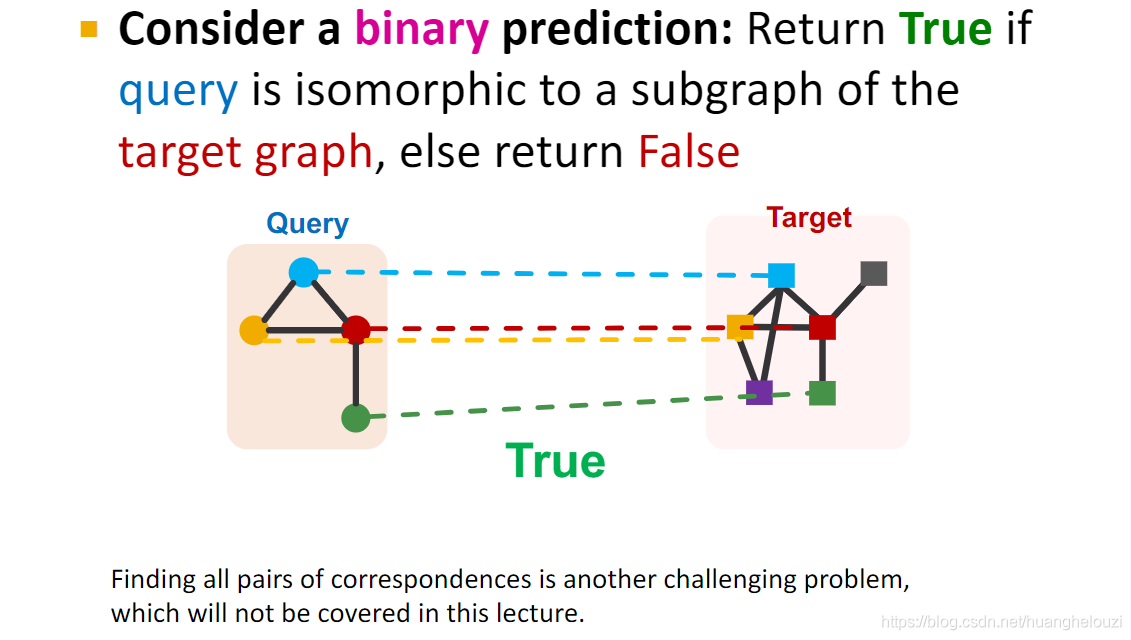
GNN完成子图匹配问题主要分为两大类，使用嵌入完成预测和普通GNN一样。



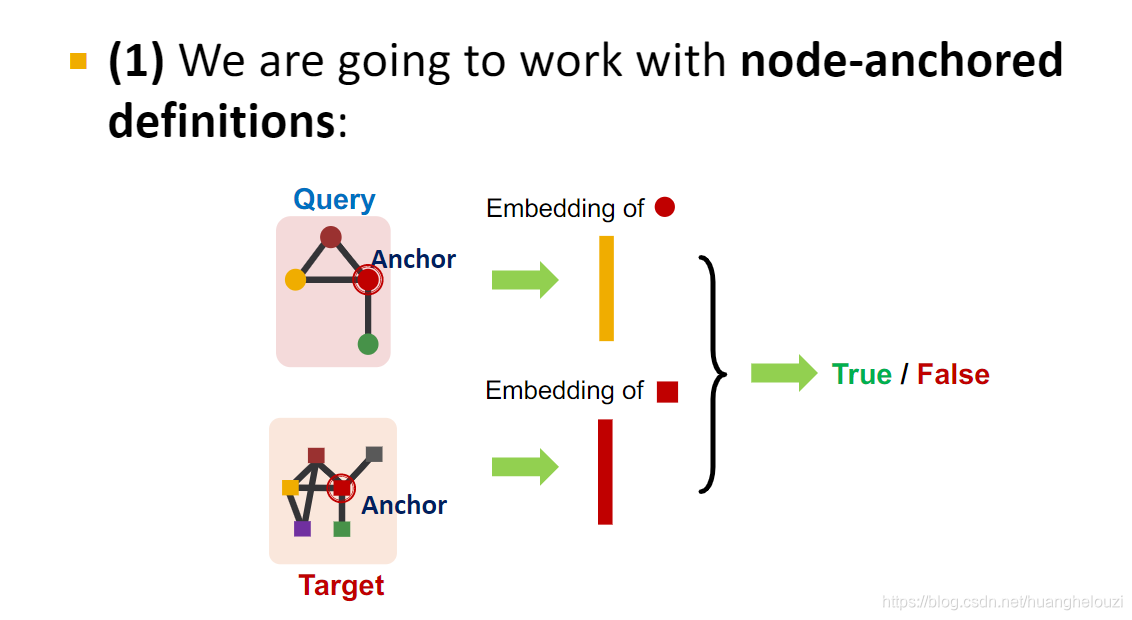
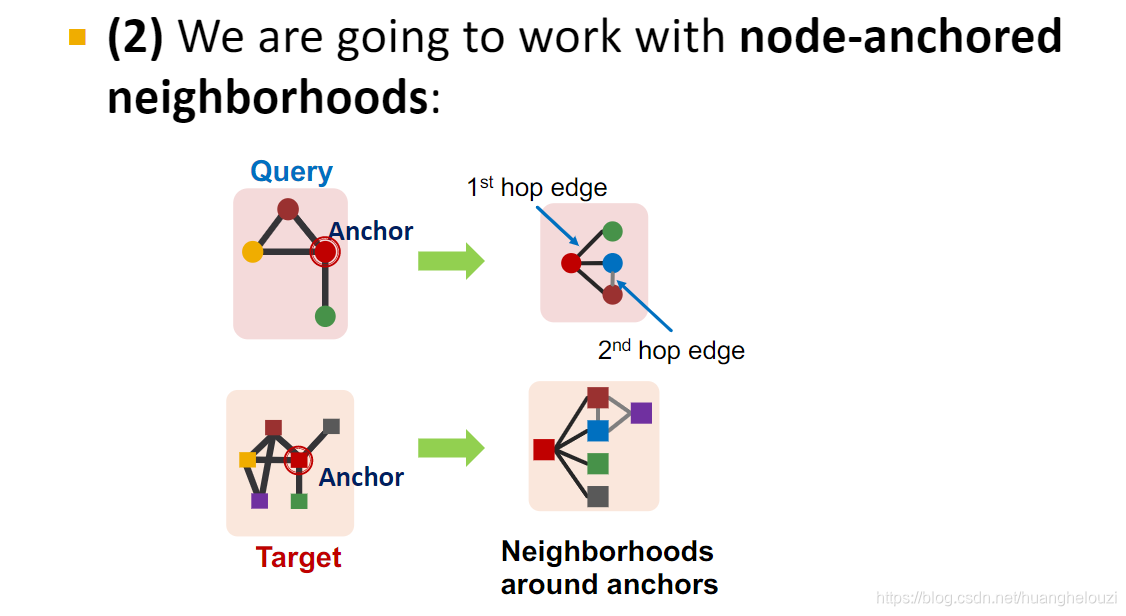
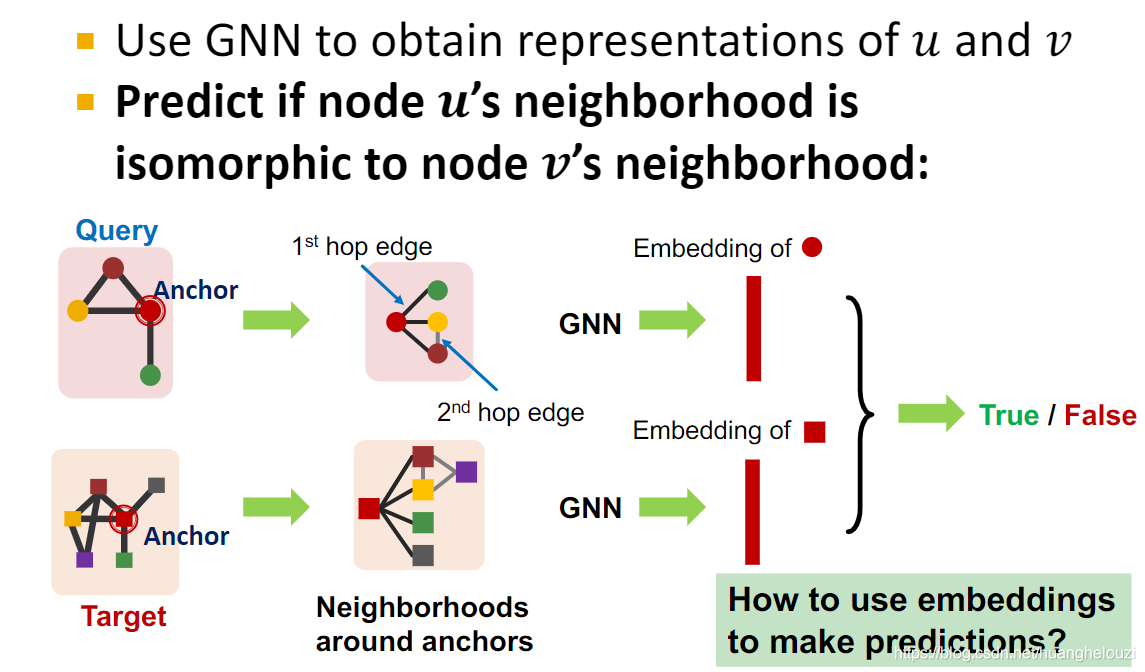
那为什么要选取锚节点呢？

对于每个锚节点，我们使用简单的广度优先搜索算法获取其周围k阶邻居。然后使用k阶邻居计算每个锚节点的嵌入。

接下来介绍有序嵌入空间（Order Embedding Space），我们需要使用GNN将图映射到这个高维的嵌入空间中，然后在这个嵌入空间中进行比较，在左下角的图（嵌入）是右上方的图（嵌入）的子图。

有序嵌入空间（Order Embedding Space）必须使得每个图嵌入的每一个维度都大于等于0，这使得我们可以通过比较嵌入的大小（也就是位置）快速正确地判断是否属于子图同构关系。同时这也使得子图关系具有传递性（transitivity），例如我们假设有三个图嵌入a、b、c，它们在有序嵌入空间的关系是a≥b，b≥c，我们可以得到a≥c，换句话说b是a的子图的同时，c又是b的子图，可以推出c也是a的子图。

举个例子，假设有两个查询图，它们的嵌入分别使用绿色圆圈和黄色圆圈表示，目标图$G_T$的嵌入使用红色方块表示。因为绿色圆圈在红色方块的左下方（绿色圆圈≤红色方块），故绿色圆圈对应的图是目标图的子图。

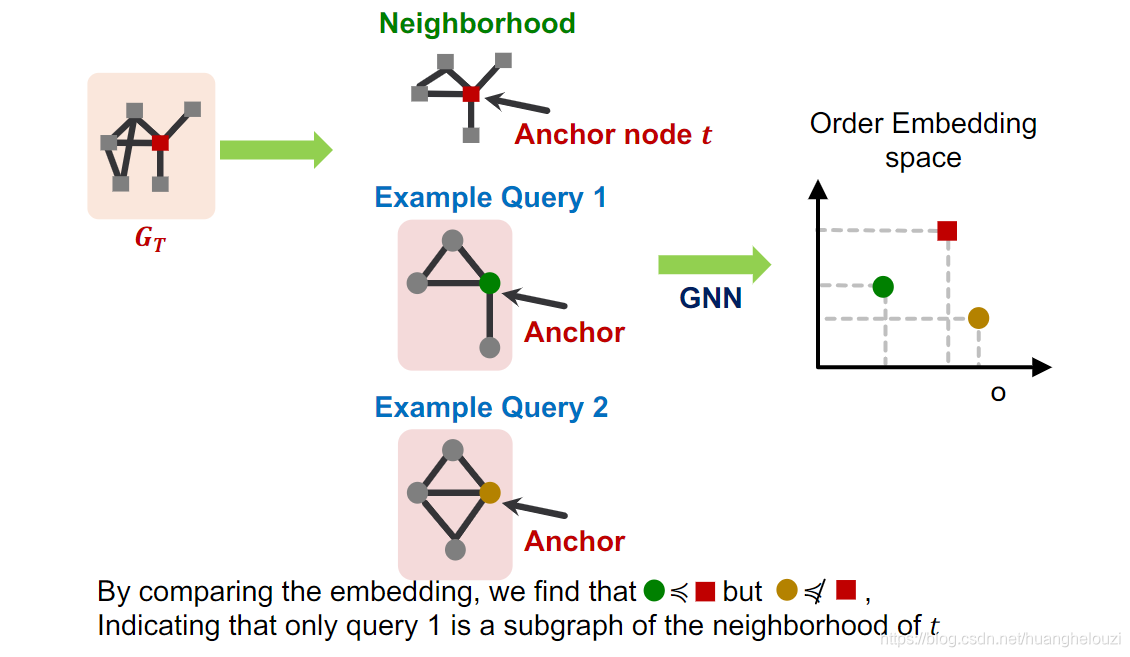
使用有序嵌入空间是因为其可以有效的编码子图同构关系。 同时有序嵌入空间还有Transitivity（传递性）、Anti-symmetry（反对称性）、Closure under intersection等特性。


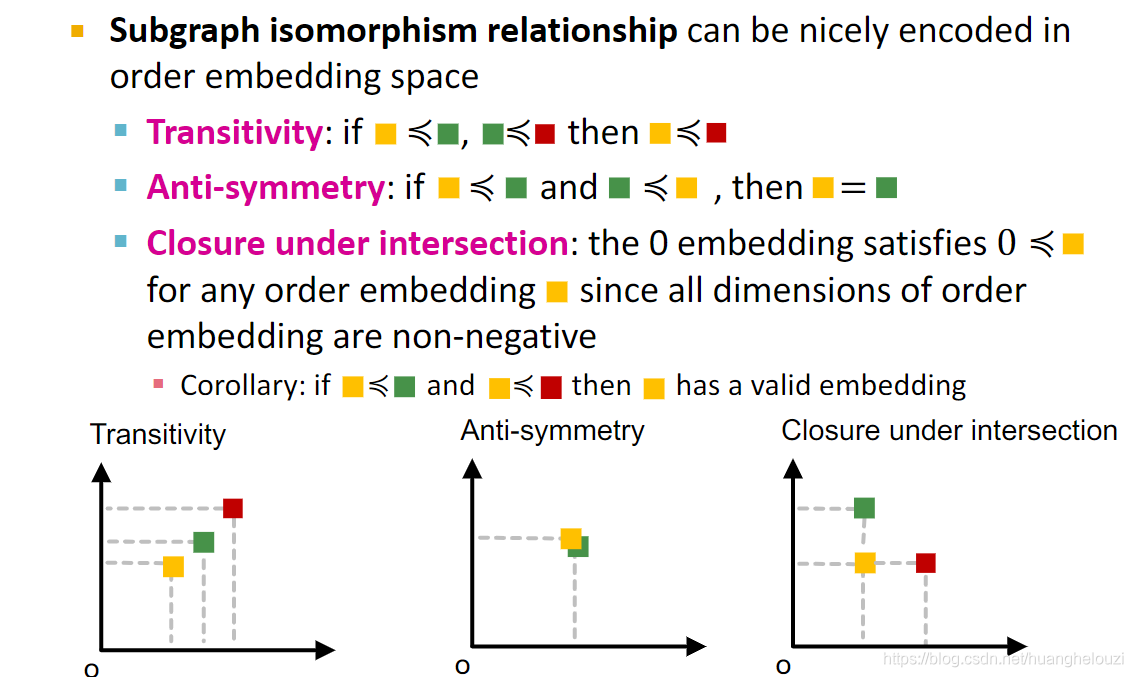
在引出GNN的Loss函数之前，先说一下有序嵌入空间的约束条件–order constraint，因为该问题的损失函数基于这个约束，这个约束应该使得我们获得的图嵌入可以很好的反应子图关系。

order constraint简而言之就是：当且仅当图$G_Q$是图$G_T$的子图时，$G_Q$的嵌入$z_q$的每一个维度上的值都小于等于图$G_T$的嵌入$z_u$对应的值，如嵌入空间是二维的，我们就可以得到$z_q$一定在$z_u$的左下方。

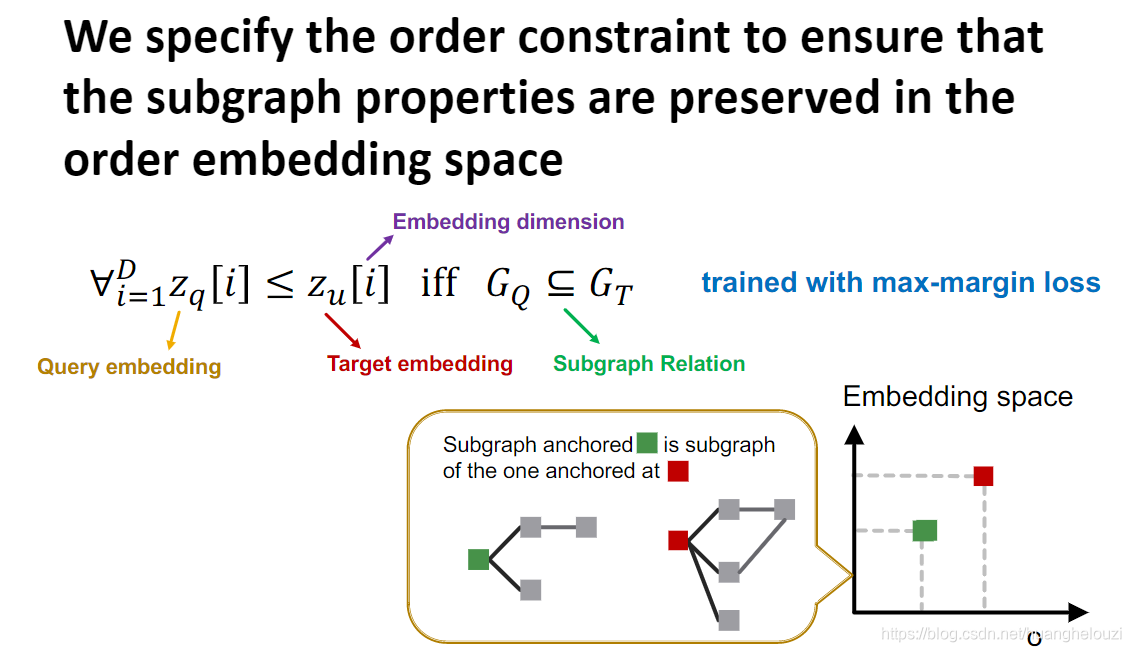
基于上面的约束order constraint我们可以设计出使用神经网络解决子图匹配问题所使用的Loss函数：max-margin loss。其中求和操作上标$D$是高维嵌入空间维数，只要子图嵌入不在目标图嵌入的左下方，必然会使得惩罚项$E(G_q,G_t)$>0，因为至少有一个维度的子图嵌入大于图嵌入的值。

在设计好损失函数后，下面给出使用解决子图匹配问题的神经网络的训练过程。注意正负样本需要保持平衡，后面也会给出正负样本采样的方法。

训练样本采样方法： 对于数据集$G$中的每一个训练样本$(G_q,G_t)$，其label取值为0或者1，1代表查询图$G_q$为目标图$G_t$的子图，0则反之。

每对正负样本由以下方法获得：
目标图$G_t$由在数据集图$G$中随机选取的锚节点(anchor) $v$以及其$k$阶邻居节点构成。

正样本查询图$G_q$（我们记为$G_{qp}$）是在目标图$G_t$中由广度优先算法以一定概率采样而得，这可以保证$G_{qp}$一定是目标图$G_t$的子图。

负样本查询图$G_q$（我们记为$G_{qn}$）是对正样本查询图$G_{q}p$进行扰动（比如加边、减边，增加节点，删除节点）得到的，这可以保证$G_{qn}$一定不是目标图$G_t$的子图。

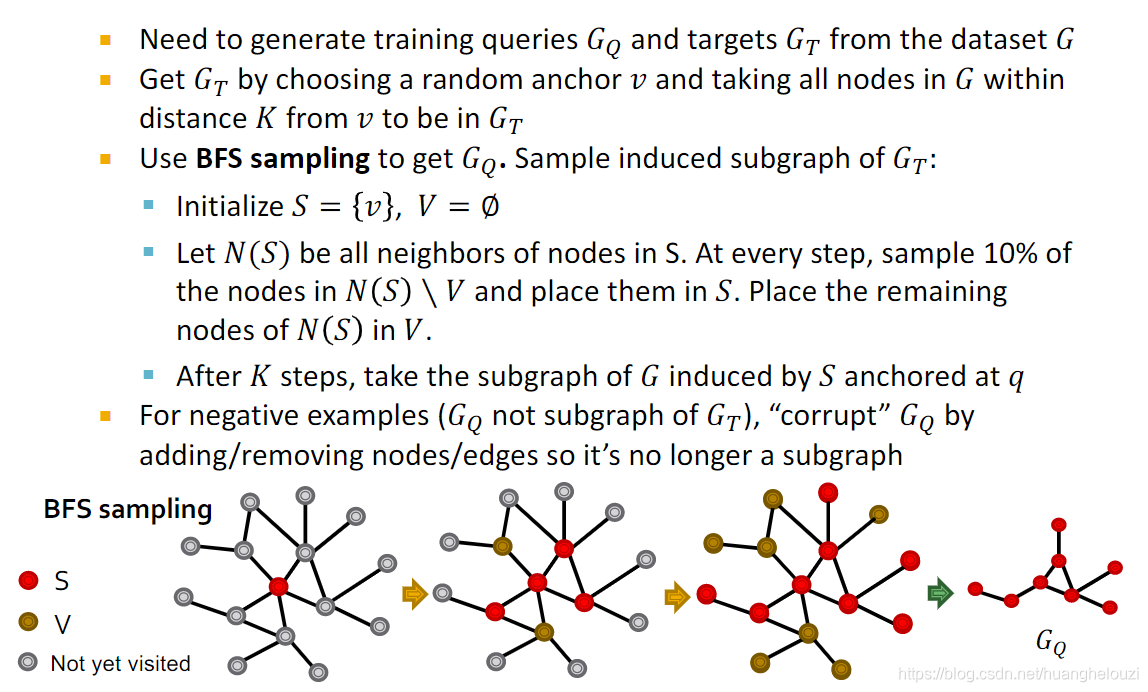
训练过程中一些细节补充：

预测新样本的过程：

下面对使用神经网络完成子图匹配问题进行一个总结：

Finding Frequent Subgraphs

寻找图中频繁出现的前k个motif是一个具有挑战性的问题，因为仅寻找一个特定motif出现的频率都是一个需要大量计算的难题。


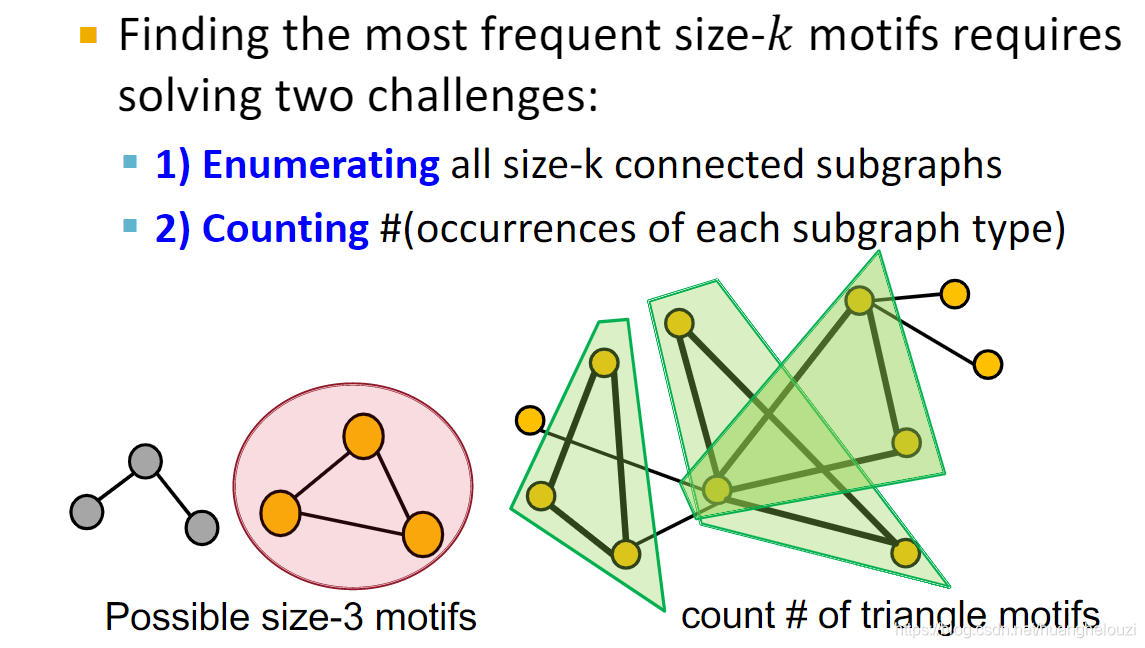
而使用神经网络（更确切的说是表征学习）来寻找频繁子图可以降低计算复杂性。

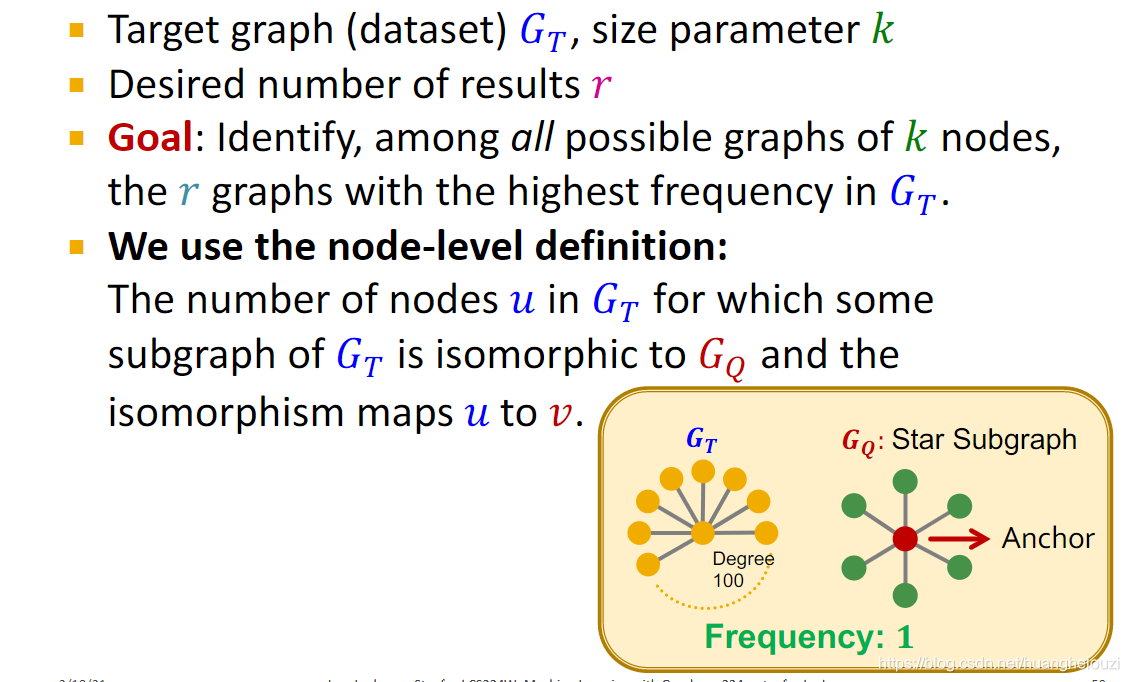
我们的目的是在目标图$G_T$中识别出频率为前$r$个且大小为$k$个节点的子图。神经网络需要学习子图的node-level嵌入，因为node-level嵌入相对来说个数比较少，可以节省很多计算资源。

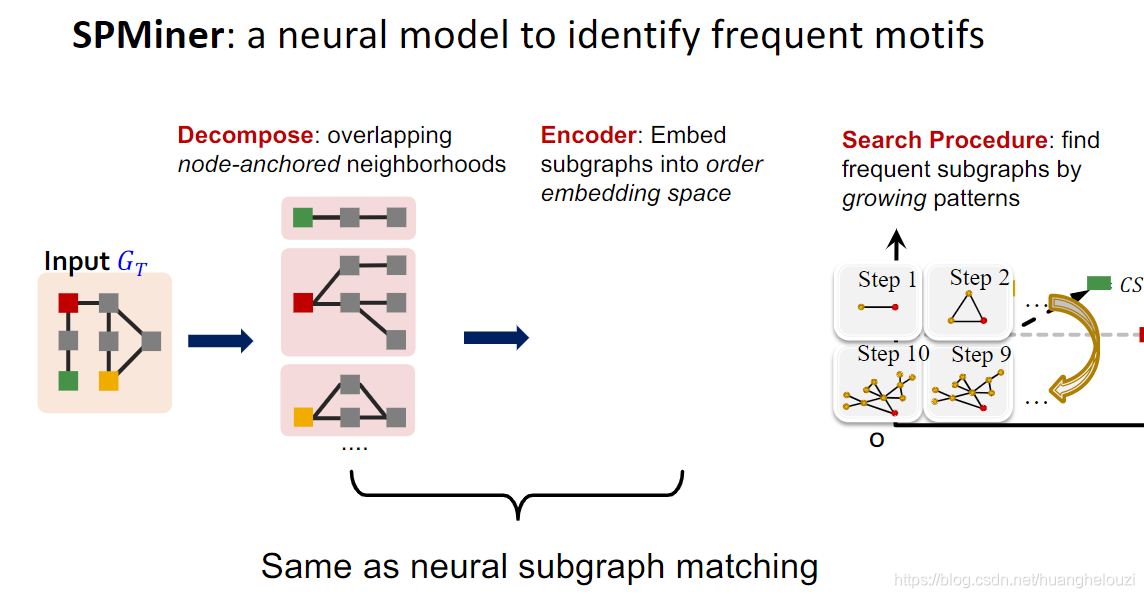
SPMiner就是一种识别高频motif的神经网络模型。SPMiner和前面所述的子图匹配神经网络是一致，创新点在最后一步“Search Procedure”。Search Procedure是一个递归的过程，第一次迭代时找出一个节点anchor（一个节点是任意图的子图），然后找出anchor直接相连的节点，使得这两个节点构成的子图为目标图的最高频子图（size=2）；第二次迭代则是找出与上一步两个节点直接相连的一个节点，使得这三个节点构成的子图为目标图的最高频子图（size=3）；依次执行，直到迭代k次，这样就找出一个由k个节点构成的最高频子图。（就是贪心算法，每一步都是当前最优的结果，故最后的结果不一定是最优的）

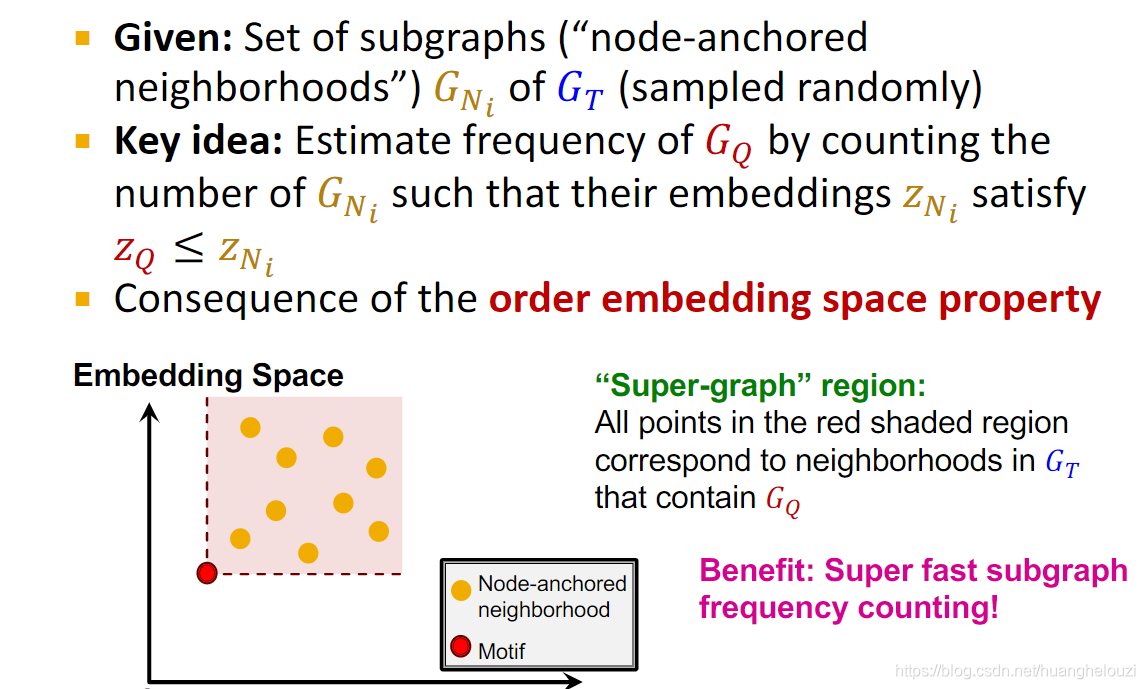
下面是SPminer的主要思想：

SPminer的嵌入目标是：使得motif的嵌入位于所有从目标图中抽样得到的子图嵌入的左下方。

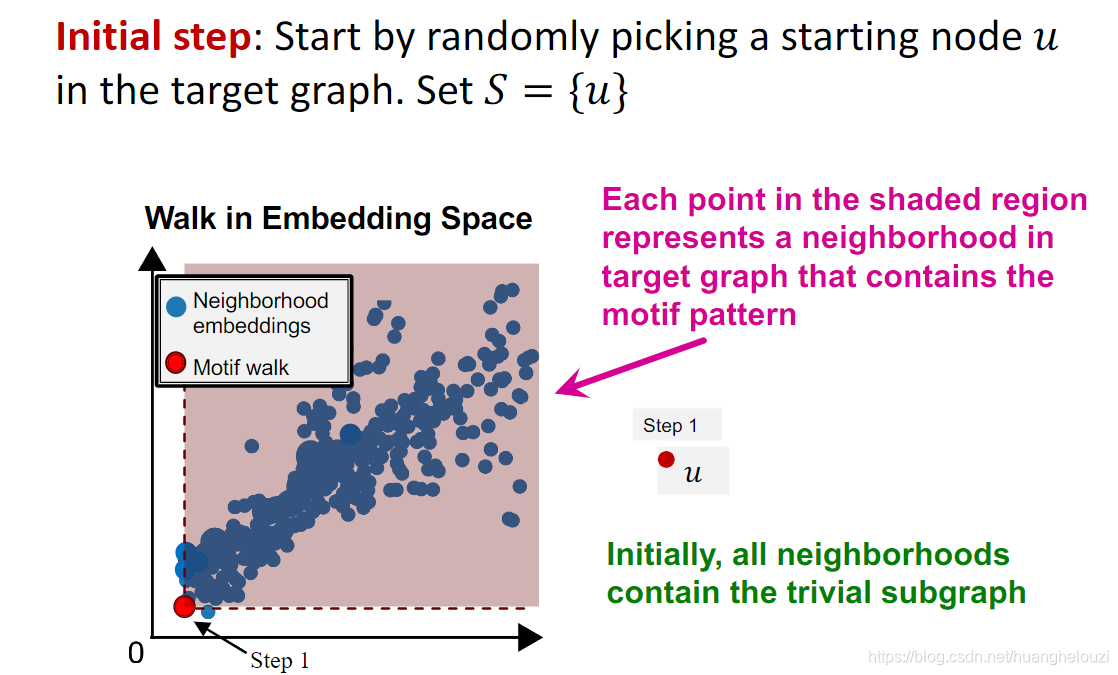
下面来详细说明Search Procedure。
在初始化时，随机选取一个节点作为锚节点。需要注意的是，单个节点一定是任意图（不包括没有节点的图）的子图

然后迭代k次，迭代过程需要满足：红色阴影区域中蓝色圈圈数量最大化。

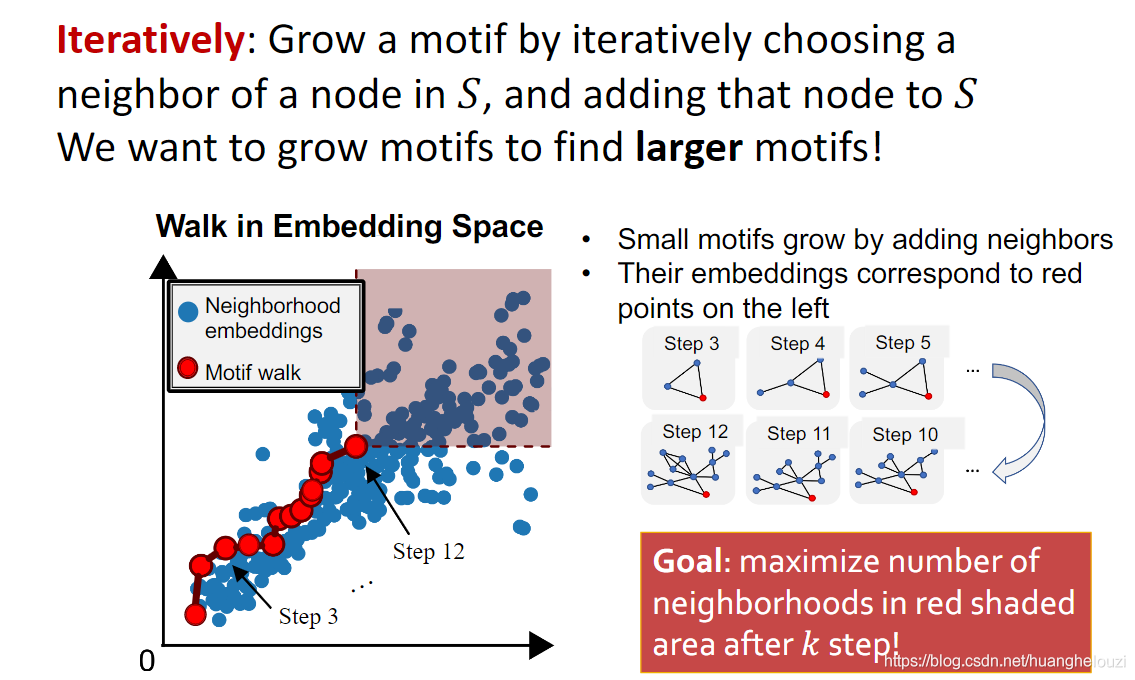
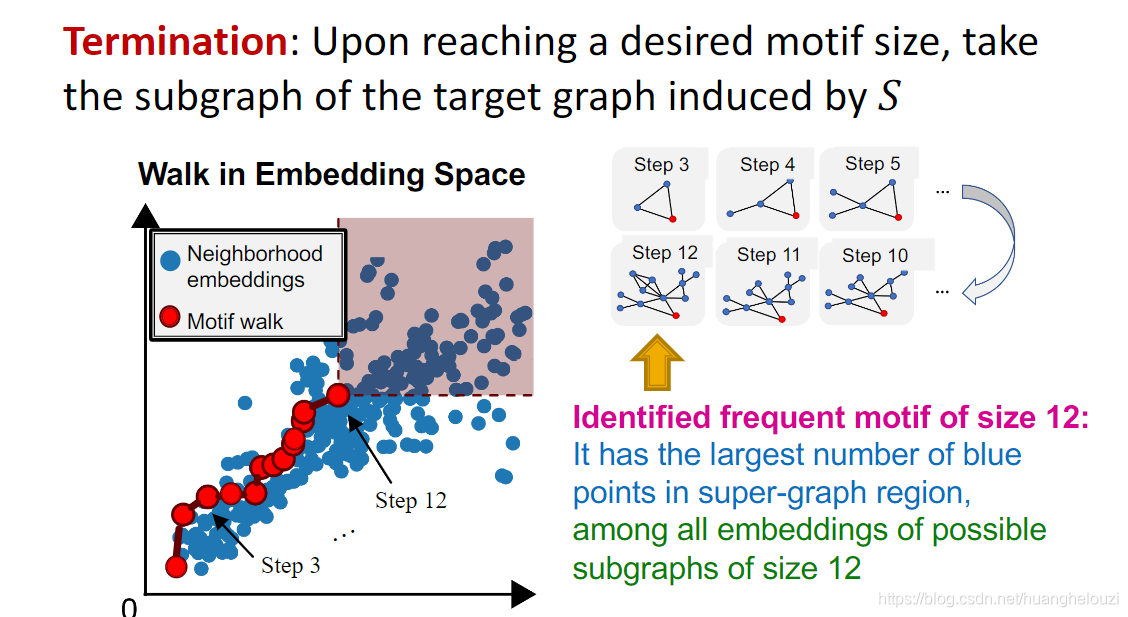
终止条件是：迭代k次，换句话说就是找到了一个节点数量为k的节点诱导子图，使得在嵌入空间中节点诱导子图右上方红色阴影区域中的绿色点数量最大化。

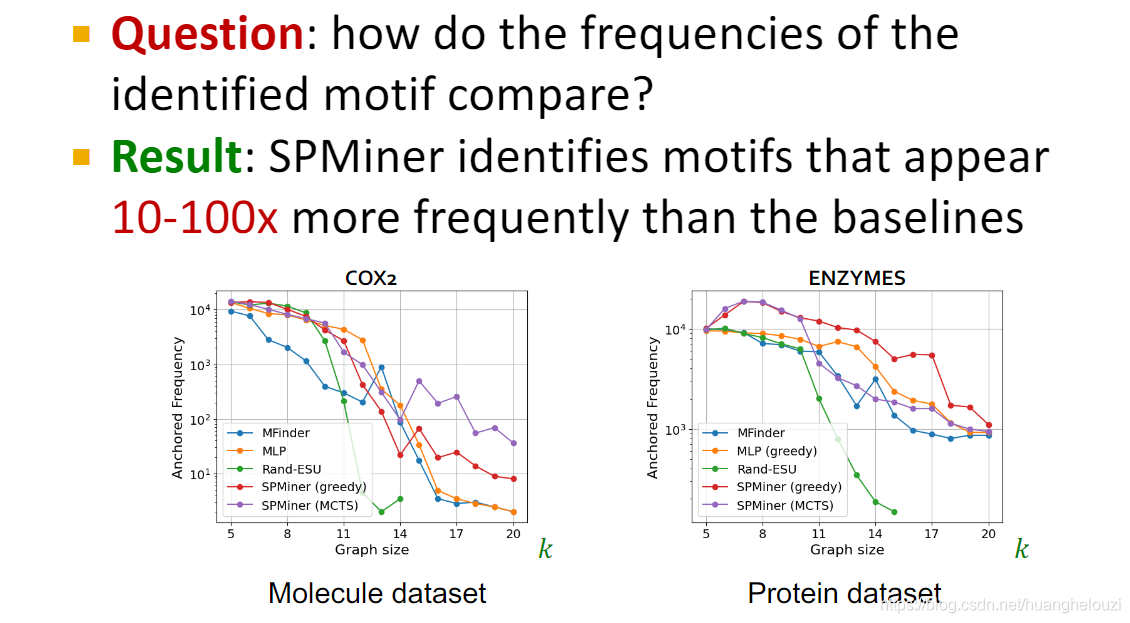
在比较小的motif中，可以发现SPMiner可以达到很高精度，分别可以找出频繁子图前十个中的前九个或者前八个。

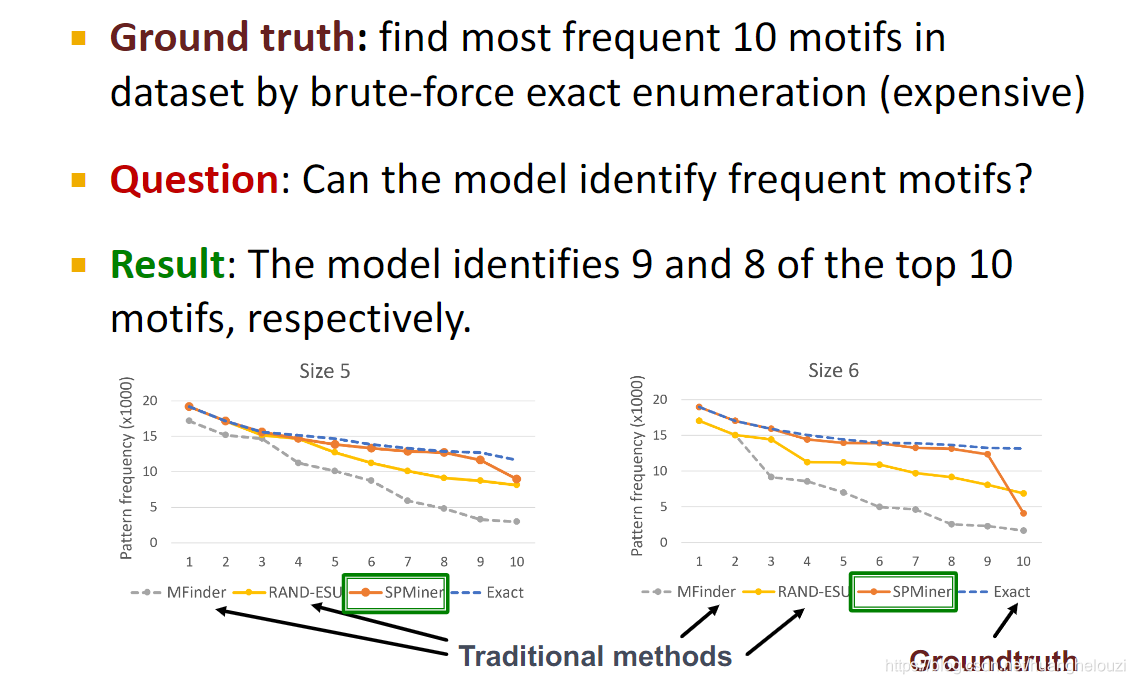
在查找大的motif时，SPMiner也明显要优于传统方法。