[人工智能]Deep Q-learning (DQN) for Multi-agent Reinforcement Learning

多智能体强化学习的深度Q学习(DQN)

背景

我们从回顾单智能体和多智能体强化学习开始。

单智能体强化学习

在单智能体、完全可观察的RL设置中，有一个智能体通过采取行动与环境交互。在每次t时，智能体观察环境的当前状态S_t ∈ S，根据随机策略π选择一个动作U_t∈ U，并接收奖励信号R_t= r(S_t，U_t)。然后，环境根据转移概率函数P(S_t+1 | S_t，U_t) 转移到新的状态S_t+1∈ S。

目标是为代理人找到一个最大化折扣回报期望的策略$\pi$，$G_t={\Sigma }_{k=t}^{\infty }{\gamma }^{k?t}{R}_t$，R_k是在时间k收到的报酬，$\gamma$∈[0,1]是一个折扣因子。策略$\pi$的作用值函数Q是Q(s，u) = E${}^{\pi }$[G_t | S_t = s，U_t = u]。

最优作用值函数$Q^{?}\sum (s,u)=ma{x}_{\pi }{Q}^{\pi }(s,u)$服从贝尔曼最优性方程$Q^{?}\sum (s,u)=r(s,u)+\gamma {\Sigma }_{s}P(s|s,u)ma{x}_{u}Q\sum (s，u)$。给定Q^*，通过选择Q函数最高的动作：${\pi }^{?}\sum (S)=argma{x}_{u}Q\sum (S，u)$，可以恢复每个状态s ∈ S的最优策略${\pi }^{?}$。这一性质导致了许多直接估计Q函数的学习算法，如Q学习沃特金斯(1989)。

Q_Learning

在Q-Learning中，代理从Q*的任意估计(Q0)开始，迭代地改进它的估计如下:在每个时间t，然后代理根据一个策略对状态栈采取一个动作ut，接收一个奖励$r_t=r(s_t，u_t)$，并观察一个新的状态s_t+1。基于经验< s_t，u_t，r_t，s_t+1 >，代理根据以下内容更新Q函数

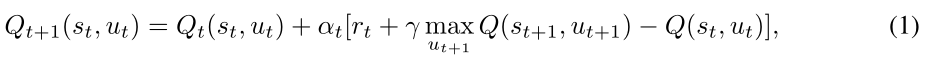
其中α_t∈(0,1)是学习速率或步长，它决定新获取的信息在多大程度上覆盖旧信息。在上述公式（1）中，术语$rt+\gamma ma{x}_{t+1}Q(s_{t+1}，u_{t+1})$被称为目标，术语$Q(s_t，u_t)$被称为估计。在迭代过程中导出新策略的一种常见方式是遵循$?$ -greedy 贪婪的策略。基于这个策略，在每个状态S_t，用概率$?$选择随机动作，概率为1-$?$，选择动作最大化Q_t。这种策略被用来引入一种探索形式，这是RL中的一个重要概念：通过根据其当前估计随机选择次优的动作，代理可以在适当的时候发现并纠正其估计。

DQN

Mnih等人(2015年)对最初的DQN提出了若干扩展。在这里，我们选择了一组扩展来解决与原始DQN相关的独特问题。

双DQN (DDQN)：在上述DQN，目标网络Q(.，.；θt)既用于选择下一状态的最佳动作，也用于计算评估所选动作的目标(见2)。这使得它更有可能选择高估的值，导致过度乐观的价值估计。为了防止这个问题，双DQN的作者在V an Hasselt等人(2016)中提出了一个简单的技巧，将动作选择从动作评估中分解出来。更具体地，在双DQN中，在线网络用于选择动作，目标网络用于生成该动作的目标值。因此，对于双DQN，式(2)中的损失可以改写如下：

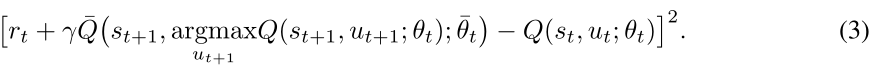
事实证明，这一变化可以大大降低DQN出现的高估，从而提高业绩。

优先体验重放：在DQN，样本是从体验重放存储器中统一随机抽取的。然而，通过同等对待所有样本，我们忽略了来自现实世界的一个简单直觉，也就是说，我们可以从结果与我们的期望相差更大的经历中潜在地学到更多。为了利用这一事实，优先经验重放(PER) Schaul等人(2015)以概率pt正比于该经验的目标值和估计值之间的绝对差异(称为TD误差)对经验进行采样。也就是说，

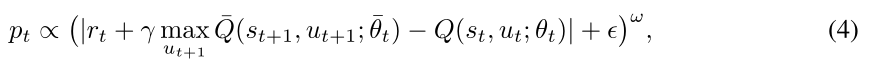
哪里$?$是一个小的正常数，确保没有经验被采样的概率为零。此外，指数ω决定使用多少优先级，ω = 0对应统一情况。对于雅达利基准套件Bellemare等人(2013年)，与统一体验重放相比，优先体验重放的使用导致了大多数游戏的更快学习和更好的最终策略质量。

决斗网络：在DQN网络体系结构中，虽然存在两个网络，即在线网络和目标网络，但是对于这些网络中的每一个，使用单个神经网络来估计动作值函数，该函数测量在特定状态下选择特定动作的值。决斗网络架构背后的关键见解王等人(2015)是，对于许多国家，没有必要估计每个行动选择的价值。为此，在这个网络体系结构中，估计了两个独立的函数，一个值函数V测量在特定状态下有多好，一个优势函数A测量在特定状态下选择特定动作的相对重要性。然后，聚合这两个函数来估计动作值函数q。例如，王等人(2015)中提出的在线网络(类似于目标网络)的聚合模块如下：

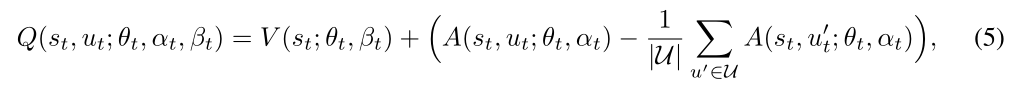
其中θ_t表示价值函数V和优势函数A的估计器之间的共享层(例如，卷积层，如果存在的话)的参数，而α_t和βt_t分别表示价值函数V和优势函数A的分离层的参数。

多智能体强化学习

在一个完全可观测的合作多智能体问题中，存在n个智能体，其中智能体的集合用A = {1，2，…，n}。在这个问题中，在每个时间点，每个代理a∈A观测环境的当前状态$S_t\in S$，并根据随机策略${\pi }_a$选择一个动作$U_t^a\in U^a$，代理的动作形成一个联合动作U_t。作为这种联合行动的结果，所有代理都收到一个奖励信号$R_t=r(S_t，U_t)$，并且环境根据转移概率函数$P(S_{t+1}|S_t，U_t)$转移到一个新的状态$S_{t+1}\in S$。目标是为所有最大化贴现收益期望的代理人找到一组策略${\pi }_a$，$G_t={\Sigma }_{k=t}^{\infty }{\gamma }^{k?t}{R}_t$，R_k是在时间k收到的报酬，γ∈(0，1)是折扣因子。

对于这样一个完全可观察的、合作的多智能体RL问题，一个自然的方法是考虑一个“元智能体”，它根据π选择联合行动U_t，π是一个包含策略${\pi }_a，a\in A$的向量，即$\pi =({\pi }_1，...，{\pi }_n)$。这个元代理学习Q函数$Q(s，u)=E^{\pi }[G_t|S_t=s，U_t=u]$，它以所有代理的状态和联合动作为条件。然后，上述针对单代理RL问题的所有算法都可以应用于该问题。然而，元代理需要选择联合动作$U_t$在${\prod }_{a\in A}{U}^a$这个空间在代理数量上呈指数增长。因此，这个问题使得这种方法不可扩展，因此对于具有大量代理的问题是不切实际的。

另一种可以应用于多智能体RL问题(不一定是完全可观察的合作问题)的方法是独立Q学习(IQL)Tan (1993)。这种方法是解决多智能体RL问题最简单也是最流行的方法，在这种方法中，每个智能体a ∈ A忽略环境中其他智能体的存在，并学习自己的Q函数$Q^a(s，u^a)=E^{{\pi }^a}[G_t|S_t=s，U_t^a=u^a]$，该函数以状态和自身的动作为条件。与第一种方法相比，IQL很有吸引力，因为它避免了上面讨论的可伸缩性问题。由于Q学习可以扩展到DQN的深层RL问题，IQL可以扩展到独立的DQN，通过让每个代理执行DQN来训练自己的神经网络来逼近自己的Q函数。

尽管IQL很简单，但它有一个关键问题：从任何代理的角度来看，环境似乎都不是固定的，因为它包含其他代理，这些代理会随着学习的进行独立更新其策略。从每个代理的角度来看，环境的非平稳性排除了Q学习存在的任何收敛保证。尽管有这个问题，IQL有强有力的实证结果马蒂尼翁等人(2012年)，然而，这样的结果不涉及深度学习。

将IQL应用于深度强化学习问题有一个关键挑战：虽然经验重放记忆的存在有助于稳定深层神经网络的训练，并且还提高了样本效率，因为它可以反复从过去的经验中重新学习，但它与IQL的结合似乎有问题。由于从IQL引入的每个代理的角度来看，环境是不稳定的，所以经验重放记忆可能不再反映代理应该学习的环境的当前动态。因此，重复使用过时的经验会不断混淆神经网络，使训练不稳定。