开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 机器学习算法 03 —— 逻辑回归算法(精确率和召回率、ROC曲线和AUC指标、过采样和欠采样) -> 正文阅读

[人工智能]机器学习算法 03 —— 逻辑回归算法(精确率和召回率、ROC曲线和AUC指标、过采样和欠采样)

系列文章

机器学习算法 01 —— K-近邻算法(数据集划分、归一化、标准化)
机器学习算法 02 —— 线性回归算法(正规方程、梯度下降、模型保存)
机器学习算法 03 —— 逻辑回归算法(精确率和召回率、ROC曲线和AUC指标、过采样和欠采样)

逻辑回归

学习目标：

知道逻辑回归的损失函数、优化?法
知道逻辑回归的应?场景
应?LogisticRegression实现逻辑回归预测
知道精确率、召回率等指标的区别
知道如何解决样本不均衡情况下的评估
会绘制ROC曲线图形

1 逻辑回归介绍

逻辑回归（Logistic Regression）是机器学习中的?种分类模型，虽然名字中带有回归，但其实是?种分类算法。由于算法的简单和?效，在实际中应??常?泛。

逻辑回归应用场景：

是否为垃圾邮件
是否患病
是否是?融诈骗
是否是虚假账号
……

看到上?的这些场景，我们可以发现其中的特点，它们都是属于两个类别之间的判断，逻辑回归就是用来解决?分类问题的。

1.1 逻辑回归原理

要掌握逻辑回归，关键是两点：

逻辑回归中，其输入值是什么？
如何判断逻辑回归的输出？

输入

逻辑回归的输入其实是一个线性回归的输出，即线性回归计算的结果。

激活函数

激活函数(sigmoid)计算公式： $g(w^T,x)=\cfrac{1}{1+e^{-h(w)}}=\cfrac{1}{1+e^{-w^Tx}}$
判断标准
- 线性回归的结果输入到sigmoid函数中
- sigmoid输出[0, 1]区间中的一个概率值，默认0.5位阀值。即输出0.6，认为是A类。

逻辑回归最终的分类是通过属于某个类别的概率值来判断是否属于某个类别，并且这个类别默认标记为1(正例)，另外的?个类别会标记为0(反例)。（?便损失计算）

输出结果解释：假设有两个类别A，B，并且假设我们的概率值为属于A(默认用1表示)这个类别的概率值。现在有?个样本的输?到逻辑回归，并输出结果0.55，这个概率值超过0.5，意味着我们训练或者预测的结果就是A类别。那么反之，如果得出结果为0.3那么，训练或者预测结果就为B(默认用0表示)类别。当然，阀值是可以改变的。

线性回归中，我们用最小二乘法衡量线性回归的损失，那么在逻辑回归中预测结果不对时，怎么衡量损失呢？例如下面图片(阀值0.6)，预测结果和真实结果存在差异，错了三个。

那么如何去衡量逻辑回归的预测结果与真实结果的差异呢？

1.2 损失以及优化

逻辑回归的损失称为对数释似然损失，公式如下：

其中 $y$ 是真实结果， $h_\theta(x)$ ?是预测结果。根据 $y$ 的类别(A类 $y = 1$ ，B类 $y = 0$ )，这个式子也分为两类。

怎么理解这个式子呢？我们根据 $\log$ ??的函数图像来看，由于两个式子前面都有负号，所以图像是 $l o g$ ??翻转过来，假设现在 $y = 1$ ?，损失函数值图像如下。（注：图像的y轴是损失函数值）

首先要明白，无论什么情况，损失函数值都是越小越好，因此现在我们讨论 $y$ ：

当 $y = 1$ ?，由图可知随着 $h_\theta(x)$ 增加，损失函数值越小。
当 $y = 0$ ，图像翻转，那么随着 $h_\theta(x)$ 减小，损失函数值越小。

所以，综合一下，完整的损失函数如下：其中， $h_\theta(x)$ 是每次预测值，y_i$是每次预测对应的真实值

现在，我们将前面的例子带入这个公式中分析损失：

既然知道了损失函数，那么我们同样可以使用梯度下降优化算法来减少损失函数的值，通过不断更新逻辑回归前面对应算法的权重参数，进行优化。提示原本属于1类别的概率，降低原本属于0类别的概率。

简单解释下上面最后一句话，在计算损失那个式子里，我们需要提高0.4的概率，因为预测的是它属于类别0，但真实结果是类别1，把0.4提升到阀值0.6，那么预测就对了。同理，我们需要降低0.68概率，提升0.41的概率。

2 逻辑回归API介绍

sklearn.linear_model.LogisticRegression(solver='liblinear', penalty=‘l2’, C = 1.0)

solver可选参数:{‘liblinear’, ‘sag’, ‘saga’,‘newton-cg’, ‘lbfgs’}，
- 默认: ‘liblinear’；?于优化问题的算法。
- 对于?数据集来说，“liblinear”是个不错的选择，?“sag”和’saga’对于?型数据集会更快。
- 对于多类问题，只有’newton-cg’， ‘sag’， 'saga’和’lbfgs’可以处理多项损失;“liblinear”仅限于“one-versus-rest”分类。
penalty：正则化的种类
C：正则化?度

默认会将类别数量少的作为正例，同时LogisticRegression?法相当于 SGDClassifier(loss=“log”, penalty=" ")，SGDClassifier实现的是?个普通的随机梯度下降学习。?LogisticRegression(实现了随机平均梯度下降)

3 案例：肿瘤良性恶性预测

原始数据下载地址：https://archive.ics.uci.edu/ml/machine-learning-databases/

网络读取数据地址：https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data

数据描述：

有699条样本，共11列数据，第?列是ID编号，后9列分别是与肿瘤相关的医学特征，最后?列是肿瘤类型数值（2良性，4恶性）。
数据集包含16个缺失值，??标出了。

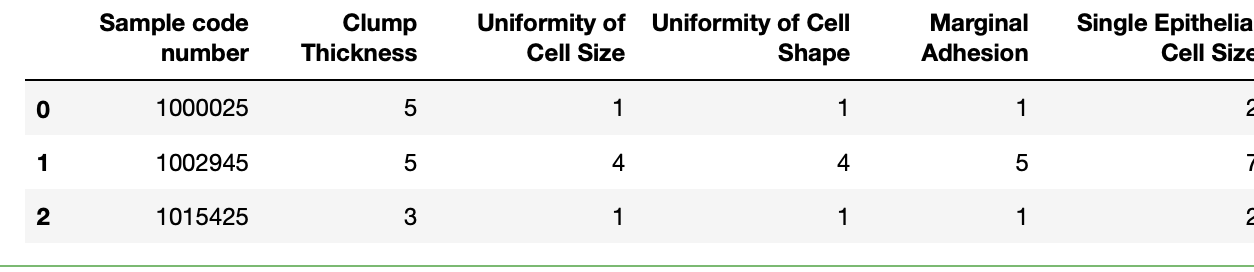
步骤分析：

1.获取数据 
2.基本数据处理 
2.1 缺失值处理(用NAN代替?，再去掉NAN)
2.2 确定特征值,?标值 
2.3 分割数据 
3.特征?程(标准化) 
4.机器学习(逻辑回归) 
5.模型评估

代码实现：

"""
肿瘤良性恶性预测
"""

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
import ssl

# 由于数据来自网络 可能出现SSL证书问题
ssl._create_default_https_context = ssl._create_unverified_context

# 1. 获取数据
# 各个列名（原始数据里没有给出列索引）
names = ['Sample code number',
         'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape',
         'Marginal Adhesion', 'Single Epithelial Cell Size', 'Bare Nuclei',
         'Bland Chromatin', 'Normal Nucleoli', 'Mitoses',
         'Class']
# 读取网络数据
data = pd.read_csv(
    "https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data",
    names=names)

# 2. 数据基本处理
# 2.1 缺失值处理 —— 将?替换为NaN，然后删除NaN
data = data.replace(to_replace="?", value=np.NaN)
data = data.dropna()
# 2.2 确定特征值(第一列不是特征值)和目标值(最后一列)以便分割数据
x = data.iloc[:, 1:10]
y = data['Class']
# 2.3 分割数据
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22, test_size=0.2)

# 3. 特征工程 —— 特征预处理 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)

# 4. 机器学习 —— 逻辑回归
estimator = LogisticRegression()
estimator.fit(x_train, y_train)

# 5. 模型评估
print("准确率：", estimator.score(x_test, y_test))
print("预测值：\n", estimator.predict(x_test))

可以发现准确率很高，但在这种分类场景中我们并不只是关注准确率，而是需要关注在所有样本中是否有全部样本都被预测出结果！！就像这个肿瘤的例子，虽然高达98%，但最后有两位患者没被预测出来，那么就不完整！！

4 分类模型的评估

对于分类模型，除了准确率，我们还需要关注其他的评估，例如精确率、召回率、F1-score等，下面进行一一介绍。

4.1 分类评估方法

混淆矩阵

在一个分类模型运行结果之下，会出现四种情况：预测为真，结果也为真，即真正例TP；预测为假，结果也为假，即真反例TN等等如下图所示。其中，TP是True Positive，FN是False Negative。

根据这四种情况，我们可以分别得出几个评估参数。

准确率

准确率：所有结果中，预测正确的结果所占的比例。即 $\frac{TP+TN}{TP+FP+TN+FN}$ ?

意义：

精确率

精确率：预测结果的正例样本中，真正例所占的比例。即 $\frac{TP}{TP+FP}$ ???。

意义：判断预测的准不准。

召回率

召回率：真实结果的正例样本中，真正例所占的比例。即 $\frac{TP}{TP+FN}$ ?

意义：判断预测的全不全面

F1-score

F1-score：即 $F_1=\frac{2TP}{2TP+FN+FP}=\frac{2\cdot精确率\cdot召回率}{精确率+召回率}$ ??，公式来源于 $\frac{2}{F_1}=\frac{1}{精确率}+\frac{1}{召回率}$

意义：反应模型的稳健性，越大，说明越稳定。

4.2 分类评估API

sklearn.metrics.classification_report(y_true, y_pred, labels=[], target_names=None )

y_true：真实?标值
y_pred：估计器预测的?标值
labels:指定类别对应的数字（案例里的2良性，4恶性）
target_names：?标类别名称（把报告结果中的2改成"良性"，4改成“恶性”）
return：每个类别精确率与召回率

修改案例，在最后增加代码：

from sklearn.metrics import classification_report

report = classification_report(y_test, y_predict, labels=(2, 4), target_names=("良性", "恶性"))

4.3 ROC曲线和AUC指标

假设样本极其不均衡：有99个恶性肿瘤样本，1个良性肿瘤样本，现在我预测全部都是恶性肿瘤，根据公式计算，准确率是99%，精确率是99%，召回率是100%，F1-score则更离谱。显然这种样本不均衡的情况下，各项指标都不靠谱。此时就要用到ROC曲线和AUC指标。

样本不均衡通常是指正例和反例的占比达到1：5或者5：1这种比较夸张的情况。

TPR与FPR

这里TPR、FPR的R是指rate，"概率"的意思。

TPR：所有真实结果为正例的样本中，预测类别为1的样本比例。其实就是召回率，即 $TPR=\frac{TP}{TP+FN}$ ???

FPR：所有真实结果为假例的样本中，预测类别为1的样本比例。即 $FPR=\frac{FP}{FP+TN}$

ROC曲线

ROC曲线是接收者操作特征曲线（receiver operating characteristic curve），是反映敏感性和特异性连续变量的综合指标。ROC曲线的横轴是FPR，纵轴是TPR。

在一个二分类模型中，假设采用逻辑回归分类器，其给出针对每个样本为正例的概率，那么通过设定一个阈值例如0.6，概率大于等于0.6的为正例，小于0.6的为假例。对应的就可以算出一组(FPR，TPR)，在平面中得到对应坐标点。
随着阈值的逐渐减小，越来越多的样本被划分为正例，但是这些正例中同样也掺杂着伪正例（TPR和FPR会增大）。阈值最大时，对应坐标点为(0,0)，阈值最小时，对应坐标点(1,1)。
当TPR和FPR相等时，即在45度对角线上时，对于不论真实结果是正例还是假例的样本，分类器预测为正例的概率是相等的，此时AUC为0.5。
理想情况下，TPR应接近1，FPR接近0，即图中的（0,1）点。ROC曲线越靠拢（0,1）点，越偏离45度对角线越好。

AUC指标

AUC（Area Under Curve）是ROC曲线下的面积（对ROC曲线求积分就能得到AUC），显然这个面积的数值不会大于1。ROC曲线一般都处于 $y = x$ ??这条直线上方，所以AUC的取值范围一般在0.5和1之间。

使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的直接说明哪个模型的效果更好，而AUC作为一个数值，可以更明了。

AUC = 1，是完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。
0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
AUC = 0.5，跟随机乱猜测一样（例：丢铜板），模型没有预测价值。
AUC < 0.5，比随机猜测还差，但只要总是反向预测而行，那么也能优于随机猜测。例如，取AUC=0，那么就是预测是正例，真实结果是反例，预测是反例，真实结果就是正例。

因此，通常来说，AUC越大的模型（分类器），正确率越高，预测效果越好！！

AUC的API如下：

导包：from sklearn.metrics import roc_auc_score

方法：sklearn.metrics.roc_auc_score(y_true, y_score)

y_true：每个样本的真实类别，只能为0(反例)、1(正例)标记。（所以案例里需要处理）
y_score：预测值，可以是正例的估计概率、置信值或者分类器?法的返回值

下面在案例里增加如下代码：

y_test = np.where(y_test > 3, 1, 0)  # 目标值2是正例，4是反例；将其转为1和0
print("AUC指标：", roc_auc_score(y_test, y_predict))

注意：AUC只能用来评价二分类，不能是多分类。AUC非常适合用于样本不均衡的模型评估。

绘制ROC曲线

现在有数据(1:1, 2:0, 3:1, 4:0, 5:0, 6:0)，冒号前面是序号，冒号后面表示真实结果是正例(1)还是反例(0)。

假设这6个数据通过模型计算出了(1:0.9, 2:0.8, 3:0.7, 4:0.6, 5:0.5, 6:0.4)，冒号前面是序号，冒号后面是概率。(设阀值为0.65)

现在对其进行ROC曲线绘制。

对概率序列按概率大小进行排序，从大到小：

序号 1 2 3 4 5 6
真实结果 1 0 1 0 0 0
预测结果 0.9 0.8 0.7 0.6 0.5 0.4
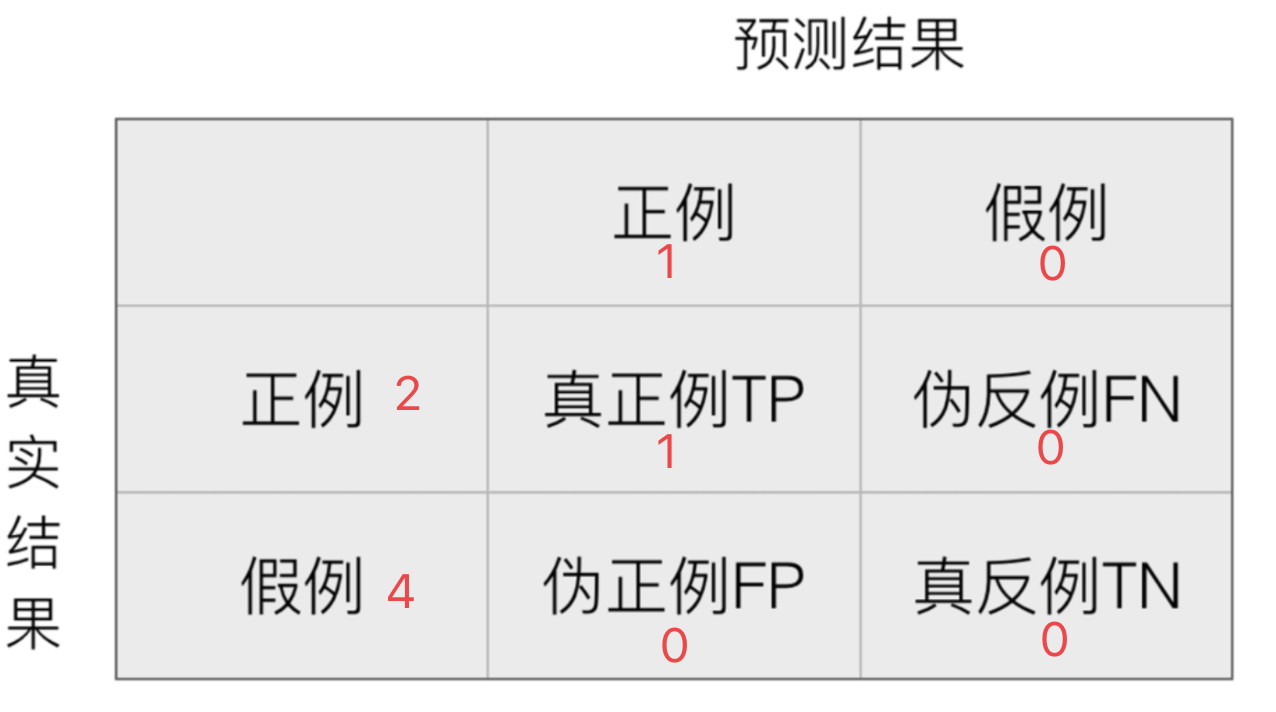
从概率最大的一点开始取点，逐一计算TPR和FPR。

点1：预测为正例，真实结果也为正例。

$FPR=\frac{FP}{FP+TN}=\frac{0}{4}=0$ ， $TPR_1=\frac{TP}{TP+FN}=\frac{1}{2}=0.5$

?

点2：预测为正例，真实结果为假例。

$FPR_2=\frac{FP}{FP+TN}=\frac{1}{4}=0.25$ ， $TPR_2=\frac{TP}{TP+FN}=\frac{1}{2}=0.5$

?

点3：预测为假例，真实结果为正例。

$FPR_3=\frac{FP}{FP+TN}=\frac{1}{4}=0.25$ ， $TPR_3=\frac{TP}{TP+FN}=\frac{2}{2}=1$
后续步骤相同，最终得到结果为：(0,0.5),(0.25,0.5),(0.25,1),(0.5,1),(0.75,1),(1.0,1.0)
将其在二维坐标系中绘制出来，其中蓝色线就是ROC曲线，其面积就是AUC值。

补充：解决类别不平衡问题

前?我们已经初步认识了，什么是数据不均衡(就是类别不平衡)问题，但并没有给出一个较好的解决方案，只是换了评估方法。其实，在现实环境中，采集到的数据往往是?例失衡的。?如?贷数据，逾期还贷的?数?例是极低的(千分之?的?例)。

对于类别不平衡的问题，主要有两种解决方法：

过采样：增加数量较少的那类样本的数量
欠采样：减少数量较多的那类样本的数量

1 构造不平衡数据集

要想解决数据不均衡问题，我们先得有一个不均衡的数据集。make_classification专门用于构建不均衡数据。

创造数据集

from sklearn.datasets import make_classification
import matplotlib.pyplot as plt

# make_classification 生成不均衡数据
X, y = make_classification(n_samples=5000, # 生成5000条数据
                           n_features=2, # 每条数据2个特征 = 2(n_informative) + 0(n_redundant) + 0(n_repeated)
                           n_informative=2, # 多信息特征的个数
                           n_redundant=0, # 冗余信息，n_informative特征的随机线性组合
                           n_repeated=0, # 重复信息，随机提取n_informative和n_redundant的特征
                           n_classes=3, # 分类类别
                           n_clusters_per_class=1, # ?个类别是由?个cluster构成的
                           weights=[0.01, 0.05, 0.94], # 3个类别的权重比
                           random_state=0 # 随机数种子
                          )

查看各个标签的样本

from collections import Counter
Counter(y) # 类别2 4674个，类别1 262个，类别0 64个

数据集可视化

plt.scatter(X[:,0], X[:,1], c=y) # c是设置颜色
plt.show()

2 解决类别不平衡的方法

需要安装imblearn包，这里用Anaconda安装下就行conda install -c glemaitre imbalanced-learn，需要注意的是目前imblearn只支持到Phthon3.6，所以有必要的话可能需要在Aanacond里创建一个新Python环境。

过采样

对训练集?的少数类进?“过采样”（oversampling），即增加?些少数类样本使得正、反例数?接近，然后再进?学习。

随机过采样

随机过采样是在少数类中随机选择?些样本，然后复制选择的样本?成样本集，将它们添加到中来扩?原始数据集从?得到新的少数类集合。

缺点：

对于随机过采样，由于需要对少数类样本进?复制来扩?数据集，造成模型训练复杂度加?。
另???也容易造成模型的过拟合问题，因为随机过采样是简单的对初始样本进?复制采样，这就使得学习器学得的规则过于具体化，不利于学习器的泛化性能，造成过拟合问题。
所以推荐使用后面的SMOTE算法

from imblearn.over_sampling import RandomOverSampler

ros = RandomOverSampler(random_state=0)
X_resampled, y_resampled = ros.fit_sample(X, y)
print(Counter(y_resampled)) # 查看各个类别数目

plt.scatter(X_resampled[:, 0], X_resampled[:, 1], c=y_resampled) 
plt.show()

SMOTE

SMOTE(Synthetic Minority Oversampling)即合成少数类过采样技术，是随机过采样?法的?个改进算法。随机过采样?法是直接对少数类进?重采?，会使训练集中有很多重复的样本，容易造成产?的模型过拟合问题。

我们?图?表达的?式，来描述?下SMOTE算法：

先随机选定?个少数类样本 $x_i$
找出这个少数类样本的K个近邻(假设K=5)，5个近邻已经被圈出。

随机从这K个近邻中选出?个样本(?绿?圈出来了)。
在少数类样本和被选中的这个近邻样本之间的连线上，随机找?点。这个点就是??合成的新的样本点（绿?正号标出）。之后如此重复，直到找齐样本集加入到原数据集中。

SMOTE算法摒弃了随机过采样复制样本的做法，可以防?随机过采样中容易过拟合的问题，实践证明此?法可以提?分类器(模型)的性能。

from imblearn.over_sampling import SMOTE

X_resampled, y_resampled = SMOTE().fit_sample(X, y)
print(Counter(y_resampled)) # 查看各个类别数目

plt.scatter(X_resampled[:, 0], X_resampled[:, 1], c=y_resampled) 
plt.show()

欠采样

对训练集中多数类样本进?“?采样”（undersampling），即去除?些多数类中的样本使得正例、反例数?接近，然后再进?学习。

随机欠采样

随机?采样顾名思义即从多数类中随机选择?些样样本组成样本集，然后将样本集从中移除，构成一个新的数据集。

缺点：

由于采样的样本集合要少于原来的样本集合，因此会造成?些信息缺失，多数类样本的删除有可能会导致分类器丢失有关多数类的重要信息。
因此通常使用过采样。

from imblearn.under_sampling import  RandomUnderSampler

rus =  RandomUnderSampler(random_state=0)
X_resampled, y_resampled = rus.fit_sample(X, y)
print(Counter(y_resampled)) # 查看各个类别数目

plt.scatter(X_resampled[:, 0], X_resampled[:, 1], c=y_resampled) 
plt.show()