论文名称:FcaNet: Frequency Channel Attention Networks
作者:Zequn Qin, Pengyi Zhang, Fei Wu, Xi Li
Code:https://github.com/cfzd/FcaNet
摘要
-
通道注意力在计算机视觉领域取得了重大成功,许多工作都致力于设计更加高效的通道注意力模块,而忽略了一个问题,使用全局平均池化作为预处理。
-
基于频率分析,本文从数学上证明了全局平均池化是频域特征分解的特例。在此基础上,推广了频域中的通道注意力预处理机制,并提出了全新的多谱通道注意力的 F c a N e t FcaNet FcaNet。
-
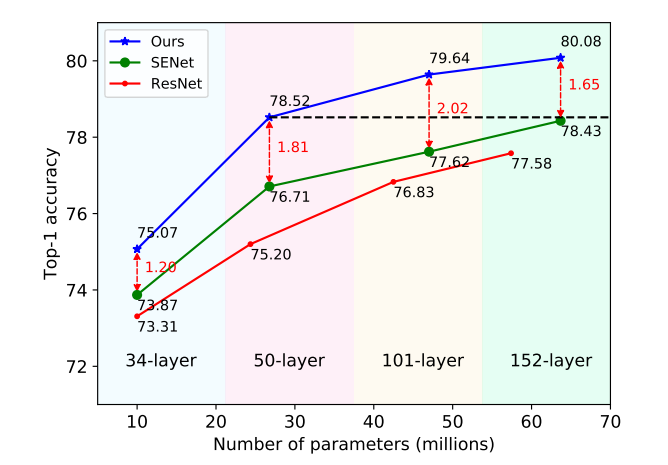
只需改变原始 S E N e t SENet SENet??中的一行代码,在图像分类、目标检测和实例分割任务上与其他信道关注方法相比取得了最先进的结果。所提出方法与基线 S E N e t ? 50 SENet-50 SENet?50 相比,在参数数量和计算成本相同的情况下,在 I m a g e N e t ImageNet ImageNet? 上的 T o p ? 1 Top-1 Top?1 精度可以提高 1.8 % 1.8\% 1.8%。
方法
动机
传统的通道注意方法致力于构建各种通道重要性权重函数,这种权重函数要求每个通道都有一个标量来进行计算,由于计算开销有限,简单有效的全局平均池化( G A P GAP GAP)成为了他们的不二之选。
但是一个潜在的问题是 G A P GAP GAP?是否能够捕获丰富的输入信息,也就是说,仅仅平均值是否足够表示通道注意力中的各个通道。
因此做了以下分析:
- 不同的通道可能拥有相同的平均值,而其代表的语义信息是不相同的;
- 从频率分析的角度,可以证明 G A P GAP GAP等价于 D C T DCT DCT??的最低频率,仅仅使用 G A P GAP GAP相当于丢弃了其他许多包含着通道特征的信息;
- C B A M CBAM CBAM还表示,仅使用 G A P GAP GAP是不够的,因此额外引入了 G M P GMP GMP?。?
分析了 G A P GAP GAP的有效性和不足之后,根据 D C T DCT DCT提出了 F c a N e t FcaNet FcaNet。?
DCT(离散余弦变换)
在介绍主要方法之前,我们需要了解一下
D
C
T
DCT
DCT?,其主要用于数据或图像的压缩,能够将空间域的信号转换到频域上,具有良好的去相关性的性能。二维的
D
T
C
DTC
DTC??公式如下:
f
h
,
w
2
d
=
∑
i
=
0
H
?
1
∑
j
=
0
W
?
1
x
i
,
j
2
d
c
o
s
(
π
h
H
(
i
+
1
2
)
)
c
o
s
(
π
h
W
(
j
+
1
2
)
)
(1)
f_{h,w}^{2d}=\sum_{i=0}^{H-1}\sum_{j=0}^{W-1}x_{i,j}^{2d}cos(\frac{\pi h}{H}(i+\frac12))cos(\frac{\pi h}{W}(j+\frac12))\tag1
fh,w2d?=i=0∑H?1?j=0∑W?1?xi,j2d?cos(Hπh?(i+21?))cos(Wπh?(j+21?))(1)
二维的逆
D
T
C
DTC
DTC公式如下:
x
h
,
w
2
d
=
∑
h
=
0
H
?
1
∑
w
=
0
W
?
1
f
i
,
j
2
d
c
o
s
(
π
h
H
(
i
+
1
2
)
)
c
o
s
(
π
h
W
(
j
+
1
2
)
)
(2)
x_{h,w}^{2d}=\sum_{h=0}^{H-1}\sum_{w=0}^{W-1}f_{i,j}^{2d}cos(\frac{\pi h}{H}(i+\frac12))cos(\frac{\pi h}{W}(j+\frac12))\tag2
xh,w2d?=h=0∑H?1?w=0∑W?1?fi,j2d?cos(Hπh?(i+21?))cos(Wπh?(j+21?))(2)
我们称二者的共有项为基函数:
B
h
,
w
i
,
j
=
c
o
s
(
π
h
H
(
i
+
1
2
)
)
c
o
s
(
π
h
W
(
j
+
1
2
)
)
B_{h,w}^{i,j}=cos(\frac{\pi h}{H}(i+\frac12))cos(\frac{\pi h}{W}(j+\frac12))
Bh,wi,j?=cos(Hπh?(i+21?))cos(Wπh?(j+21?))
下面证明
G
A
P
GAP
GAP是二维
D
C
T
DCT
DCT的特例,令
h
,
w
h,w
h,w都为
0
0
0?:
KaTeX parse error: No such environment: align at position 8: \begin{?a?l?i?g?n?}? f_{0,0}^{2d} &…
这代表着二维
D
C
T
DCT
DCT???变换的最低频率分量,因此
S
E
N
e
t
SENet
SENet?可以表示为:
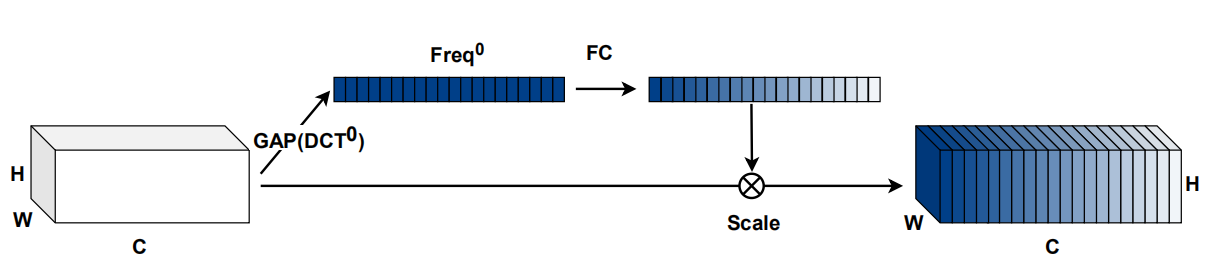
根据公式 ( 2 ) (2) (2)????我们可以知道特征可以被分解为不同频率分量的组合,自然而然地,可以将其在通道注意力上进行推广——使用多个频率分量。
Multi-Spectral Attention Module
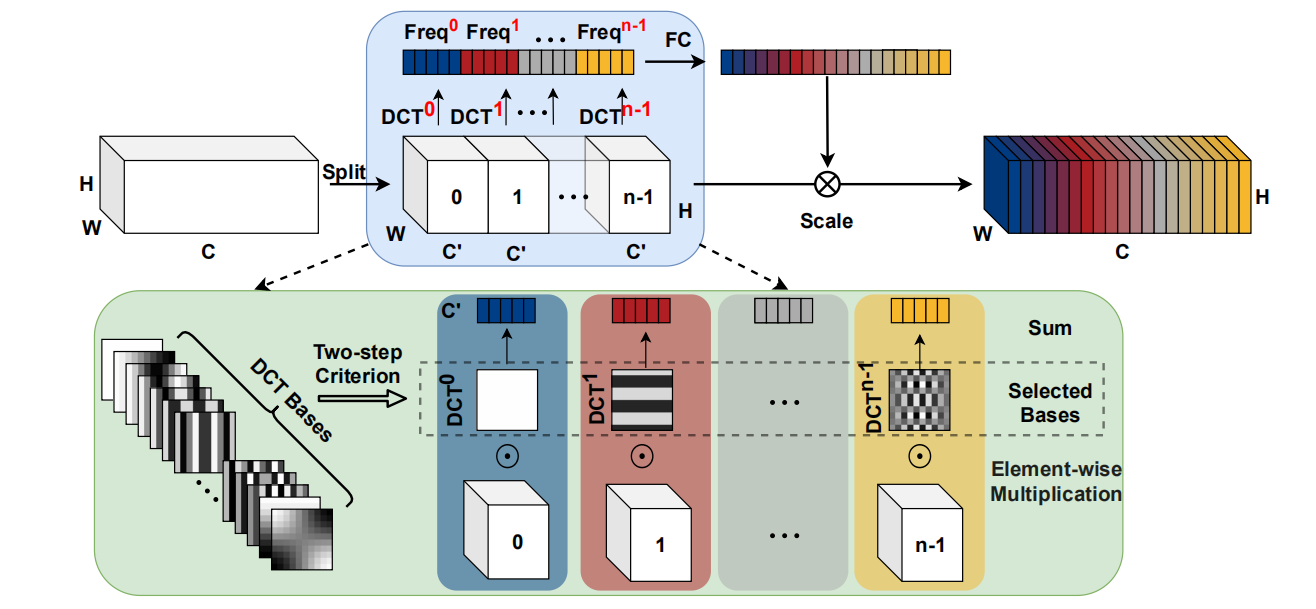
主要分为以下两个步骤:
- 将输入分组,选取不同频率分量
- 与 S E N e t SENet SENet????两层的 M L P MLP MLP得到通道注意力权重
并且只要修改一行代码就可以实现:

但实际上并没有这么简单
选择哪些频率分量?
频率分量的选择显得十分 E m p i r i c a l l y Empirically Empirically
首先验证单个频率分量的效果,作者在 R e s N e t 50 ResNet50 ResNet50上将 I m a g e N e t ImageNet ImageNet最小映射到了 7 × 7 7\times 7 7×7????的大小,这意味着总共有 49 49 49?种频率分量,最终结果如下图所示:
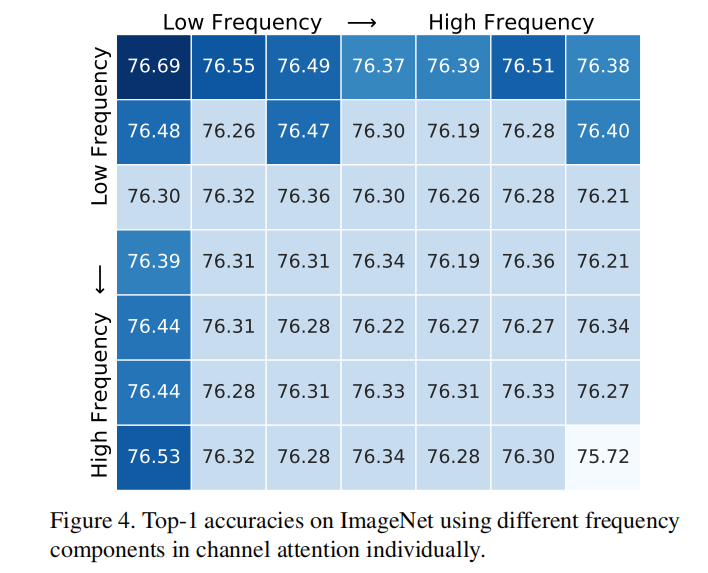
可以发现低频分量拥有更好的表现,这同时验证了 S E N e t SENet SENet??的成功,此外,可以表明其他频率分量也拥有良好的性能。
至于多种频率分量的组合过于复杂,因此提出以下三种方法来进行组合: l o w ? k low-k low?k?, t o p ? k top-k top?k??, b o t ? k bot-k bot?k??
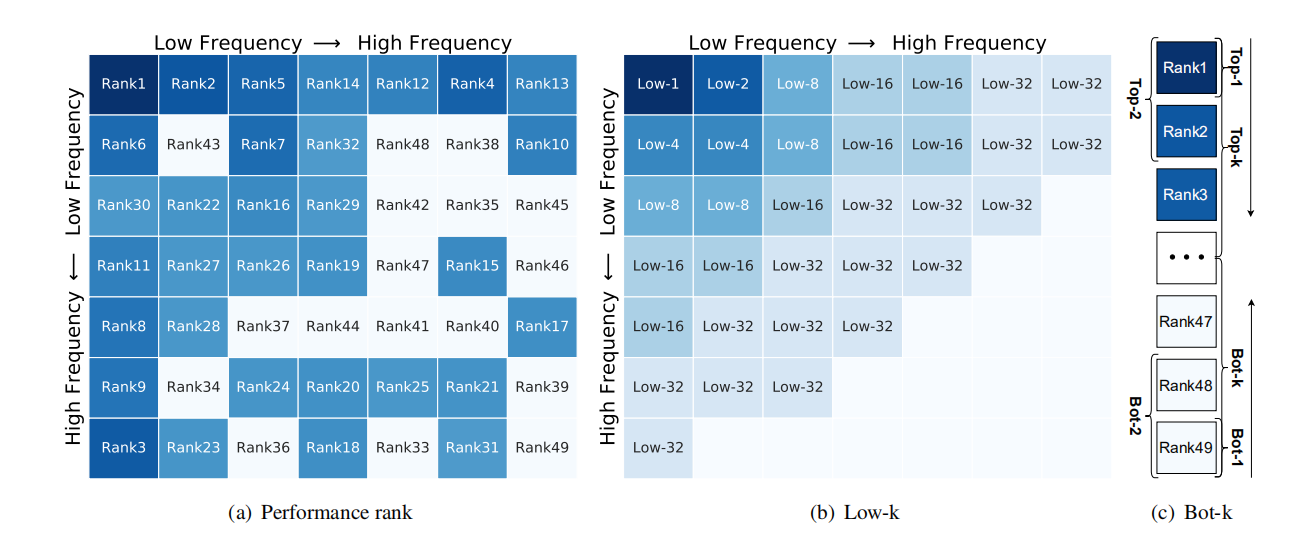 l
o
w
?
k
low-k
low?k:根据频率由低到高选取
l
o
w
?
k
low-k
low?k:根据频率由低到高选取
t o p ? k top-k top?k:根据上文的性能排名由高到低选取
b o t ? k bot-k bot?k:根据上文的性能排名有低到高选取
实验结果如下:
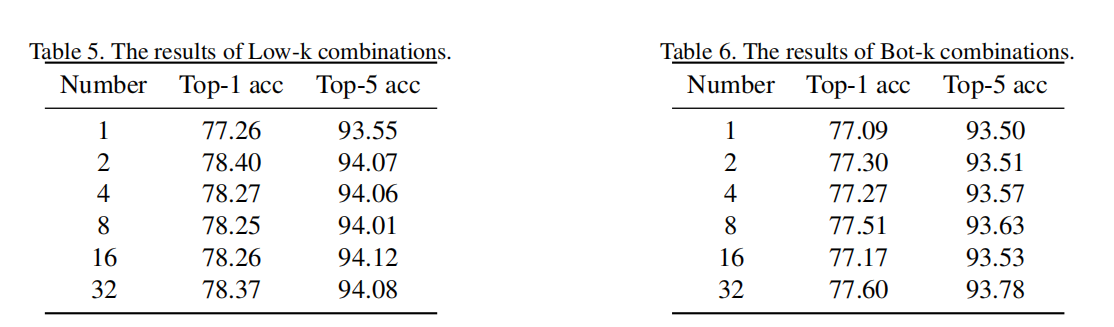
这仍然表明低频分量的重要性
并且发现 t o p ? 16 top-16 top?16的效果最好:
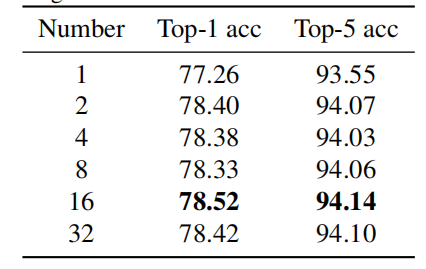
如何获得DCT权重
首先获得选取的频率分量的“坐标”:
def get_freq_indices(method): # 获得分量排名的坐标
assert method in ['top1', 'top2', 'top4', 'top8', 'top16', 'top32',
'bot1', 'bot2', 'bot4', 'bot8', 'bot16', 'bot32',
'low1', 'low2', 'low4', 'low8', 'low16', 'low32']
num_freq = int(method[3:])
if 'top' in method:
all_top_indices_x = [0, 0, 6, 0, 0, 1, 1, 4, 5, 1, 3, 0, 0,
0, 3, 2, 4, 6, 3, 5, 5, 2, 6, 5, 5, 3, 3, 4, 2, 2, 6, 1]
all_top_indices_y = [0, 1, 0, 5, 2, 0, 2, 0, 0, 6, 0, 4, 6,
3, 5, 2, 6, 3, 3, 3, 5, 1, 1, 2, 4, 2, 1, 1, 3, 0, 5, 3]
mapper_x = all_top_indices_x[:num_freq]
mapper_y = all_top_indices_y[:num_freq]
elif 'low' in method:
all_low_indices_x = [0, 0, 1, 1, 0, 2, 2, 1, 2, 0, 3, 4, 0,
1, 3, 0, 1, 2, 3, 4, 5, 0, 1, 2, 3, 4, 5, 6, 1, 2, 3, 4]
all_low_indices_y = [0, 1, 0, 1, 2, 0, 1, 2, 2, 3, 0, 0, 4,
3, 1, 5, 4, 3, 2, 1, 0, 6, 5, 4, 3, 2, 1, 0, 6, 5, 4, 3]
mapper_x = all_low_indices_x[:num_freq]
mapper_y = all_low_indices_y[:num_freq]
elif 'bot' in method:
all_bot_indices_x = [6, 1, 3, 3, 2, 4, 1, 2, 4, 4, 5, 1, 4,
6, 2, 5, 6, 1, 6, 2, 2, 4, 3, 3, 5, 5, 6, 2, 5, 5, 3, 6]
all_bot_indices_y = [6, 4, 4, 6, 6, 3, 1, 4, 4, 5, 6, 5, 2,
2, 5, 1, 4, 3, 5, 0, 3, 1, 1, 2, 4, 2, 1, 1, 5, 3, 3, 3]
mapper_x = all_bot_indices_x[:num_freq]
mapper_y = all_bot_indices_y[:num_freq]
else:
raise NotImplementedError
return mapper_x, mapper_y
根据公式进行计算,在空间维度上进行求和,得到DCT权重:
class MultiSpectralDCTLayer(nn.Module):
"""
Generate dct filters
"""
def __init__(self, height, width, mapper_x, mapper_y, channel):
super(MultiSpectralDCTLayer, self).__init__()
assert len(mapper_x) == len(mapper_y)
assert channel % len(mapper_x) == 0
self.num_freq = len(mapper_x)
# fixed DCT init
self.register_buffer('weight', self.get_dct_filter(
height, width, mapper_x, mapper_y, channel)) # 对应于公式中的H,W,i,j,C
# fixed random init
# self.register_buffer('weight', torch.rand(channel, height, width))
# learnable DCT init
# self.register_parameter('weight', self.get_dct_filter(height, width, mapper_x, mapper_y, channel))
# learnable random init
# self.register_parameter('weight', torch.rand(channel, height, width))
# num_freq, h, w
def forward(self, x):
assert len(x.shape) == 4, 'x must been 4 dimensions, but got ' + \
str(len(x.shape))
# n, c, h, w = x.shape
x = x * self.weight
result = torch.sum(x, dim=[2, 3]) # 在空间维度上求和
return result
def build_filter(self, pos, freq, POS): # 对应i/j, h/w, H/W
result = math.cos(math.pi * fre关于q * (pos + 0.5) /
POS) / math.sqrt(POS) # 基函数公式的一半
if freq == 0:
return result # 对应gap的形式
else:
return result * math.sqrt(2) #
def get_dct_filter(self, tile_size_x, tile_size_y, mapper_x, mapper_y, channel): # 对应与H,W,i,j,C
dct_filter = torch.zeros(channel, tile_size_x,
tile_size_y) # 对于每一个BATCH都是相同的
c_part = channel // len(mapper_x) # 每一份的通道长度
for i, (u_x, v_y) in enumerate(zip(mapper_x, mapper_y)):
for t_x in range(tile_size_x):
for t_y in range(tile_size_y):
dct_filter[i * c_part: (i+1)*c_part, t_x, t_y] = self.build_filter(
t_x, u_x, tile_size_x) * self.build_filter(t_y, v_y, tile_size_y) # 将f的求和式展开,储存在一个图中,这里实际上是一个3维的,因为这些通道的权重相同,最后再乘以原图求和得到f
return dct_filter
网络效果
I m a g e N e t ImageNet ImageNet分类:
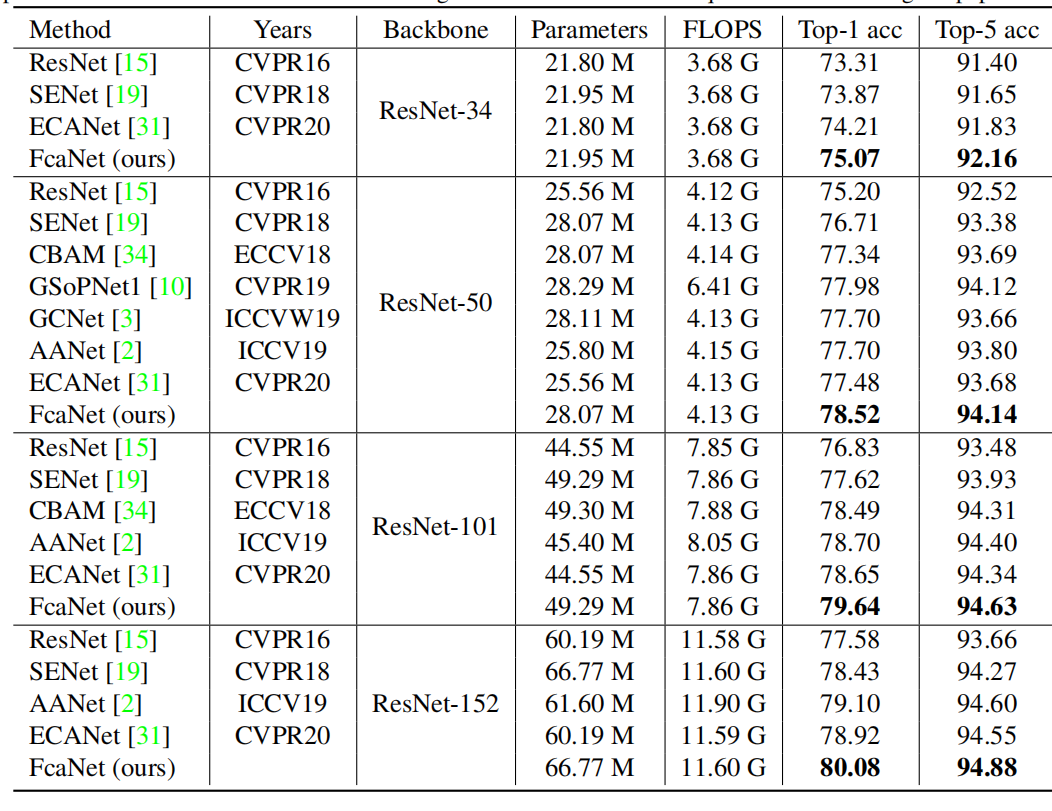
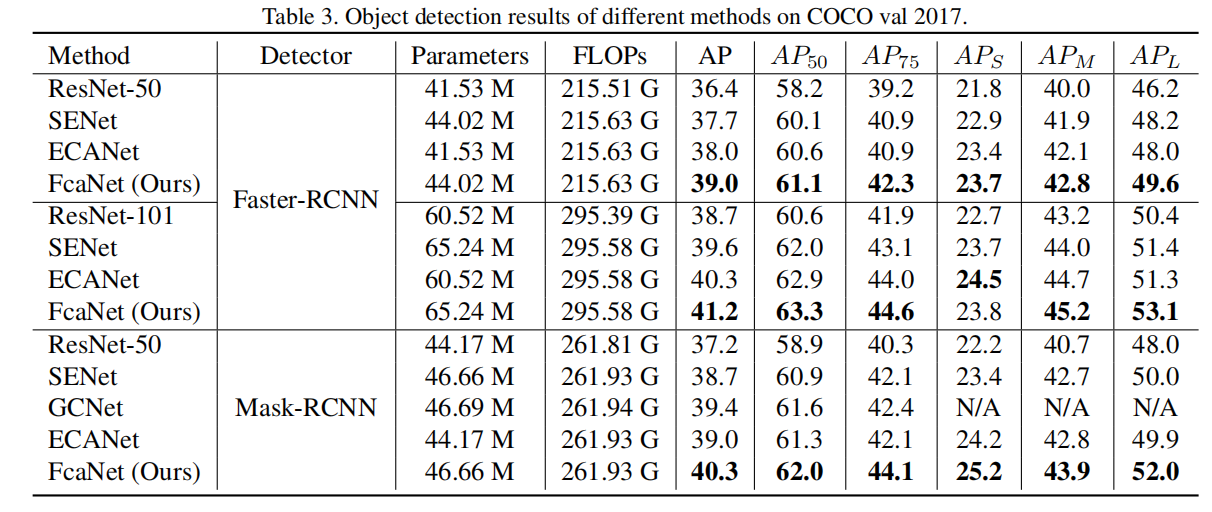
C O C O COCO COCO目标检测:
一些思考
关于将通道分组,使用不同的频率分量加权,但是这些分量单独的效果都没有 G A P GAP GAP??好,而就结果而言,效果却明显好与GAP的 S E N e t SENet SENet,可能是引入不同的频率分量增加了通道注意力的多样性,由于使用了全连接层,其可以凭借更多的信息来得到权重。
其次,是否应该是对所有的通道进行不同的频率分量加权,因为不同通道上表示的信息不同,如何保证不会有更多信息的丢失,有人提出了同样的问题
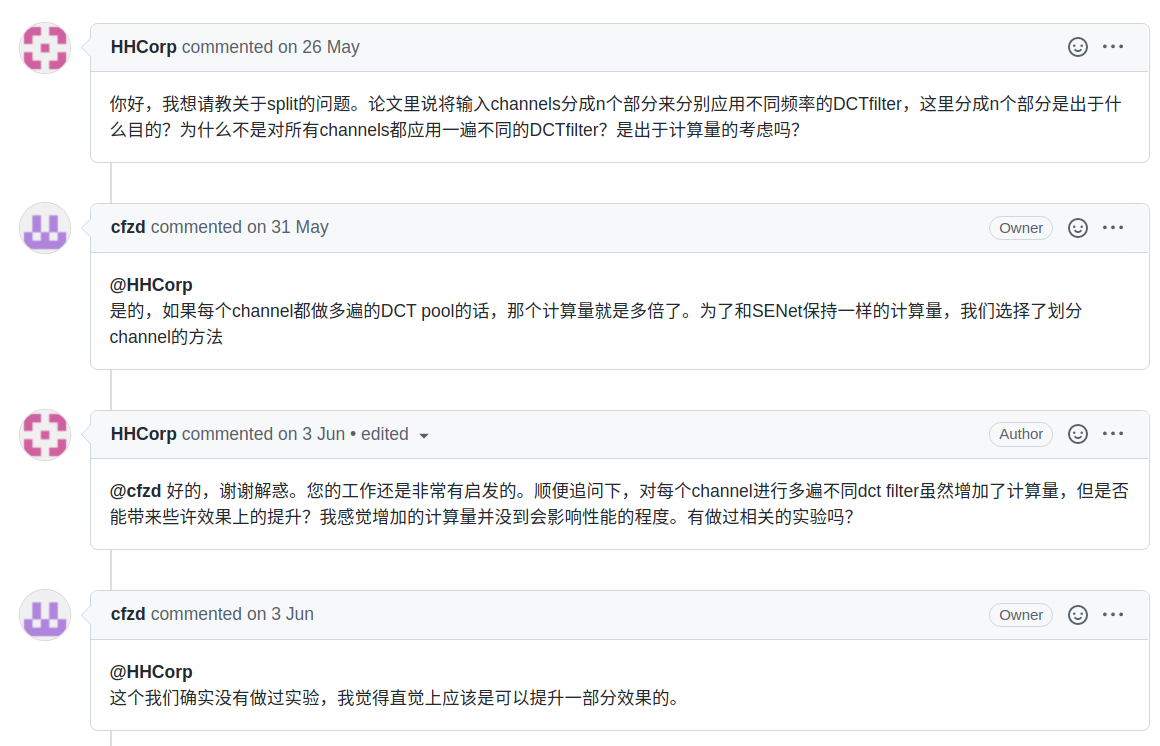
这一点可能是因为事件空间不同,DCT可以看作一种加权和,我们知道注意力模块会学习一种X到Y的映射,仅仅使用GAP可能会导致输入空间过小,换句话说就是输入向量不够稀疏,导致结果也较为相近。其中加权和的权值可视化如下:
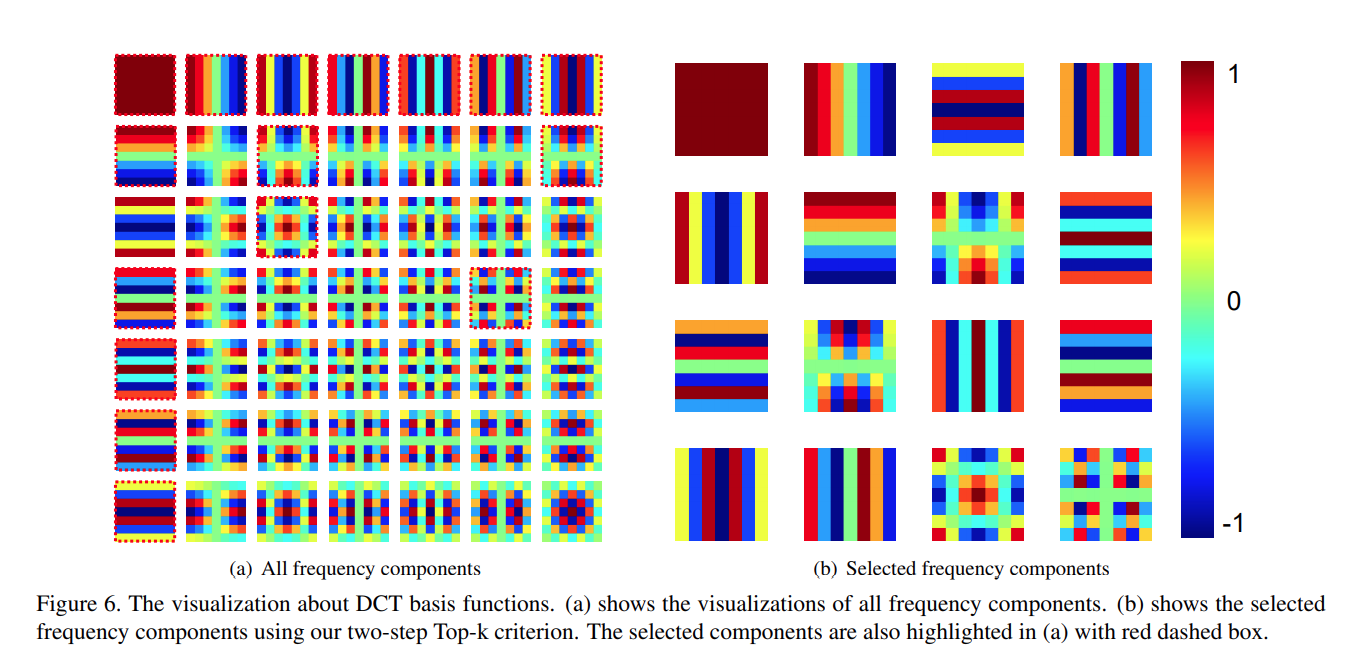
另外,感觉这或许与Sinusoidal Position Embedding有些相似