插值算法是图像处理中最基本的算法,首先我们先了解一下什么是插值算法,以及插值算法在图像处理过程中的应用。
1、什么是插值
Interpolation is a method of constructing new data points within the range of a discrete set of known data points. Image interpolation refers to the “guess” of intensity values at missing locations.
在日常对图像进行操作的过程中会涉及到图像的放大与缩小,这一系列的操作都是通过插值法来实现的;opencv中resize()函数的实现原理0就是通过插值算法,如果不对应用某种算法进行设置,则默认采用双线性插值算法。
简单来说,插值指利用已知的点来“猜”未知的点,图像领域插值常用在修改图像尺寸的过程,由旧的图像矩阵中的点计算新图像矩阵中的点并插入,不同的计算过程就是不同的插值算法。

2、常用的插值算法
最近邻法(Nearest Interpolation):计算速度最快,但是效果最差。
双线性插值(Bilinear Interpolation):双线性插值是用原图像中4(22)个点计算新图像中1个点,效果略逊于双三次插值,速度比双三次插值快,属于一种平衡美,在很多框架中属于默认算法。
双三次插值(Bicubic interpolation):双三次插值是用原图像中16(44)个点计算新图像中1个点,效果比较好,但是计算代价过大。
3、最近邻插值(Nearest Interpolation)
“近邻”,顾名思义就是从原图像矩阵中找到与它(目标图像的像素点)距离最近的点,然后将最近点的像素值,赋给它就行了。
那么如何找最近点?
假设目标图像与原图像的坐标点的对应关系如下:
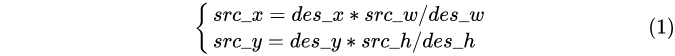
其中
[src_x] : 原图像中像素点 [x] 坐标
[src_y] : 原图像中像素点 [y] 坐标
[des_x] : 目标图像中像素点 [x] 坐标
[des_y] : 目标图像中像素点 [y] 坐标
[src_w] : 原图像宽度(width)
[src_w] : 原图像高度(high)
[des_w] : 目标图像宽度(width)
[des_w] : 目标图像高度(high)

下面简述一下如何计算:
目标像素坐标 → 原图像像素坐标
注:如果坐标为小数,四舍五入即可。
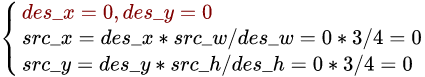

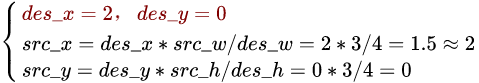
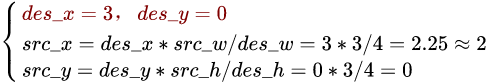
上面已计算出目标图像的第一行像素点坐标对应于原图像的坐标. 其余的坐标对应关系也可上述方法依次计算.
最近邻插值缺点:最邻近算法计算量较小,但可能会造成插值生成的灰度上的不连续,在灰度变化的位置处,可能会产生明显的锯齿现象.
4、双线性插值
双线性插值的对应公式和前面的最近邻法一样,不一样的是根据对应关系不再是找最近的1个点,而是找最近的4个点,如下图所示

这里可能还会有点小疑问,如果根据对应关系找到原图中的点不是在不同的点之间,而是跟原图像中的点重合,那该如何找4个点?关于这个问题要看一下双线性插值的计算公式,双线性插值实际上是从2个方向一共进行了3次单线性插值,咱们先了解单线性插值的计算方式。
4.1 单线性插值
已知中P1点和P2点,坐标分别为(x1, y1)、(x2, y2),要计算 [x1, x2] 区间内某一位置 x 在直线上的y值

根据初中的知识,2点求一条直线公式(这是双线性插值所需要的唯一的基础公式)
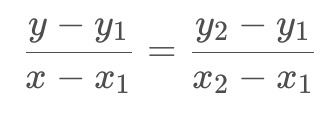
整理后:
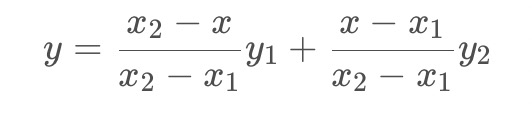
这里没有写成经典的AX+B的形式,因为这种形式从权重的角度更好理解。
首先看分子,分子可以看成x与x1和x2的距离作为权重,这也是很好理解的,P点与P1、P2点符合线性变化关系,所以P离P1近就更接近P1,反之则更接近P2。
现在再把公式中的分式看成一个整体,原式可以理解成y1与y2是加权系数,如何理解这个加权,要返回来思考一下,咱们先要明确一下根本的目的:咱们现在不是在求一个公式,而是在图像中根据2个点的像素值求未知点的像素值。这样一个公式是不满足咱们写代码的要求的。
现在根据实际的目的理解,就很好理解这个加权了,y1与y2分别代表原图像中的像素值,上面的公式可以写成如下形式:
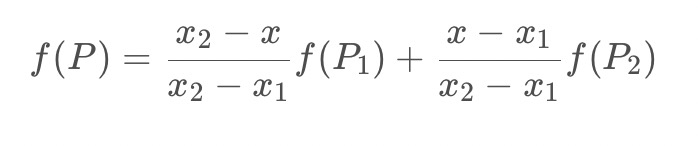
4.2 双线性插值
已知Q11(x1,y1)、Q12(x1,y2)、Q21(x2,y1)、Q22(x2,y2),求其中点P(x,y)的值。

前面介绍过双线性插值是分别在两个方向计算了共3次单线性插值,如图所示,先在x方向求2次单线性插值,获得R1(x, y1)、R2(x, y2)两个临时点,再在y方向计算1次单线性插值得出P(x, y)(实际上调换2次轴的方向先y后x也是一样的结果)。
1.x方向单线性插值 直接带入前一步单线性插值最后的公式

2. y方向单线性插值
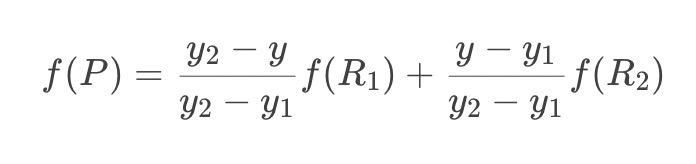
将第一步结果带入第二步
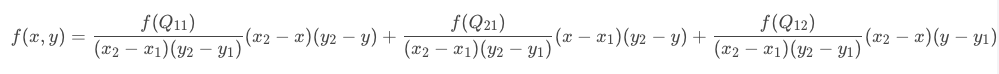
回顾一下上面双线性插值对应关系的图,不难发现,在计算中有这样的关系:
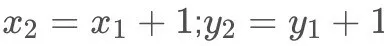
那么上面的公式中的分母全都为0,如下:

在有些资料中,会写成权重的形式,上面的展开式是下面的权重表达式的正确求法
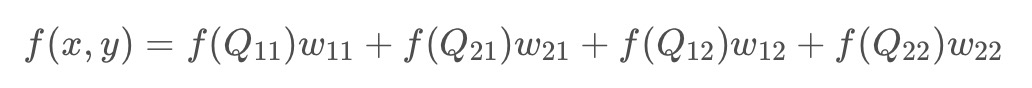
f(x,y)代表目标图像上坐标为(x,y)的值。
参考博客链接:
https://zhuanlan.zhihu.com/p/110754637
https://zhuanlan.zhihu.com/p/266951945