[人工智能]朴素贝叶斯算法(上)

算法篇

朴素贝叶斯算法

朴素贝叶斯算法属于有监督学习中的分类算法，基于贝叶斯理论和特征相互独立的假设，因为假设特征相互独立让问题变得简单，因此称为朴素
要使用朴素贝叶斯算法，首先要了解的就是概率。
条件概率公式：

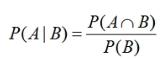
当A、B相互独立时，$P(AB)=P(A)?P(B)$

全概率公式：

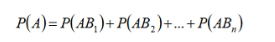
贝叶斯公式：

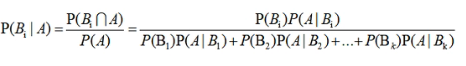
朴素贝叶斯计算步骤：

1. 一个数据集中有两个样本(B1，B2， B3)、(C1，C2，C3)和一个标签的两组(A1，A2)
2. 给定一个测试样本(D1，D2，D3)，使用贝叶斯公式求出测试样本属于A1组还是A2组
   $P(A1|测试特征)=\frac{P(测试特征,A1)}{P(测试特征)}=\frac{P(A1)?P(测试特征|A1)}{P(测试特征)}$
   $P(A2|测试特征)=\frac{P(测试特征,A2)}{P(测试特征)}=\frac{P(A2)?P(测试特征|A2)}{P(测试特征)}$
3. 由于两式分母都是相同的，所以只需要考虑分子就可以了
   $P(A1|测试特征)=P(测试特征,A1)=P(A1)?P(测试特征|A1)$
   $P(A2|测试特征)=P(测试特征,A2)=P(A2)?P(测试特征|A2)$
4. 这时遇到一个问题，如果所选特征在训练集中不存在，$P(测试特征|A1)$将会等于0，最终的概率也会等于0，显然这样的结果不是我们想要的
5. 这就需要我们引入特征相互独立的假设了
   $P(AB)=P(A)?P(B)$
   $P(测试特征|A1)=P(D1,D2,D3|A3)=P(D1|A1)?P(D2|A1)?P(D3|A1)$
   $P(A1|测试特征)=P(测试特征,A1)=P(A1)?P(D1|A1)?P(D2|A1)?P(D3|A1)$
   $P(A2|测试特征)=P(测试特征,A2)=P(A2)?P(D1|A2)?P(D2|A2)?P(D3|A2)$
6. 根据在训练集数据就可以计算出A1的概率以及A1的条件下D1、D2、D3发生的概率了
7. 虽然是能计算出来，但是可能会出现D1这个特征没有出现在训练集特征的情况，比如D1=高，恰好A1组相应类型特征对应的数据低，它的概率也会变成0
8. 这是就出现了一个拉普拉斯系数，当测试集特征不存在时，给它变成1，相应的分母也要加一。例如，测试集某个特征不存在，概率本应该是$\frac{0}{n}$，使用拉普拉斯系数后就变成了$\frac{1}{n+1}$，一旦有一个是找不到的，所有测试集特征都要分子分母各加一

伯努利朴素贝叶斯

伯努利分布又称0-1分布，也叫二项分布，所以伯努利朴素贝叶斯只能对符合二分类数据的特征
伯努利分布公式：

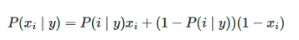
和上面朴素贝叶斯计算步骤有所不同的是，拉普拉斯系数不同。伯努利中的拉普拉斯，分母计算方法是符合计算标签结果的特征条数加上标签类别数，分子还是加1。比如，标签是下雨和没雨，现在判断的是下雨的条件下特征发生的概率，符合条件的训练集特征有4条，分母就是4+2=6。

代码实现

from sklearn.naive_bayes import BernoulliNB
# 实例化
alg = BernoulliNB()
# 参数：alpha，默认是等于拉普拉斯，防止等于零的情况出现

# 拟合
alg.fit(X_train, y_train)

# 预测结果
y_pred = alg.predict(X_test)
print('预测结果：', y_pred)

# 预测概率
print('预测概率：', alg.predict_proba(X_test))

# 查看准确率
score = alg.score(X_test, y_test)
print('准确率：', score)

高斯朴素贝叶斯

高斯朴素贝叶斯主要是用来处理连续数据类型的特征
概率密度函数：

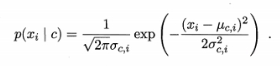
μ代表均值，σ代表标准差

代码实现

from sklearn.naive_bayes import GaussianNB
# 实例化
alg = GaussianNB()
# 参数：alpha，默认是等于拉普拉斯，防止等于零的情况出现

# 拟合
alg.fit(X_train, y_train)

# 预测结果
y_pred = alg.predict(X_test)
print('预测结果：', y_pred)

# 预测概率
print('预测概率：', alg.predict_proba(X_test))

# 查看准确率
score = alg.score(X_test, y_test)
print('准确率：', score)