一、线性模型
1、线性回归模型
(1)、遍历法寻找最优参数
给出一些点,例如:
| X | Y |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | ? |
我们需要做的就是利用已给出的训练数据中的规律,来尽可能精准的计算出未知的需要计算的值。
形如:
Y
=
w
x
+
b
\\Y=wx+b
Y=wx+b
为线性模型
训练的方法为先给定参数 w,b的范围,遍历这个范围,找到输入X后输出最符合Y值的w,b参数。 那么如何判断是最符合的呢? 一般采用的方法是采用输入X,计算出y_p ,然后使用y_p和给定的y值来计算两个数之间的误差。 误差的计算方法是
l
o
s
s
=
(
y
p
?
y
)
2
\\ loss=(y_p-y)^2
loss=(yp??y)2
计算出所给出的输出和给定输出之间误差之和最小的一组w,b的值,即为最优的w,b的取值。当使用这组w,b时,我们的预测将会是最准的。
##未使用pytorch
import numpy as np
import matplotlib.pyplot as plt
x_data=[1.0,2.0,3.0]##准备训练数据
y_data=[2.0,4.0,6.0]##测试
def forward(x):##预测函数
return x*w##由于很明显所给数据符合wx,股不写b
def loss(x,y):##判断误差
Y_PRED=forward(x)
return (y-Y_PREDIT)**2
w_list=[]
loss_list=[]
for w in np.arange(1.0,2.1,0.1):
print("w=",w)
l_sum=0
for x_var,y_var in zip(x_data,y_data):
y_pred_var = forward(x_var)
loss_var=loss(x_var,y_var)
l_sum+=loss_var
print('\t',x_var,y_var,y_pred_var,loss_var)
w_list.append(w)
loss_list.append(l_sum/3)
plt.plot(w_list,loss_list)
plt.show()
输出结果
##有删减
w= 1.0
1.0 2.0 1.0 1.0
2.0 4.0 2.0 4.0
3.0 6.0 3.0 9.0
w= 1.1
1.0 2.0 1.1 0.8099999999999998
2.0 4.0 2.2 3.2399999999999993
3.0 6.0 3.3000000000000003 7.289999999999998
w= 1.9000000000000008
1.0 2.0 1.9000000000000008 0.00999999999999984
2.0 4.0 3.8000000000000016 0.03999999999999936
3.0 6.0 5.700000000000003 0.08999999999999829
w= 2.000000000000001
1.0 2.0 2.000000000000001 7.888609052210118e-31
2.0 4.0 4.000000000000002 3.1554436208840472e-30
3.0 6.0 6.000000000000003 7.099748146989106e-30
w= 2.100000000000001
1.0 2.0 2.100000000000001 0.010000000000000196
2.0 4.0 4.200000000000002 0.040000000000000785
3.0 6.0 6.3000000000000025 0.0900000000000015
w= 2.200000000000001
1.0 2.0 2.200000000000001 0.040000000000000424
2.0 4.0 4.400000000000002 0.1600000000000017
3.0 6.0 6.600000000000003 0.3600000000000038
w= 3.0000000000000018
1.0 2.0 3.0000000000000018 1.0000000000000036
2.0 4.0 6.0000000000000036 4.000000000000014
3.0 6.0 9.000000000000005 9.000000000000032
图像也可以更直观的表现出平均损失与w值的关系,
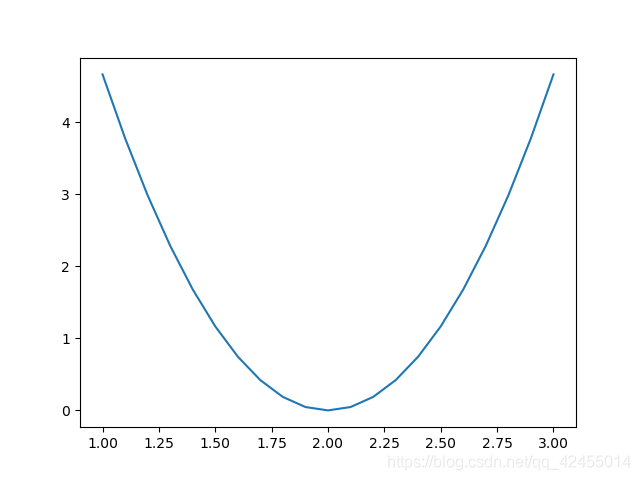
当w=2.0时,平均损失最小,故w取2.0时是最优解。
上面例子稍加修改就可以变成 y=wx+b的标准形式进行预测
(2)、梯度下降
虽然我们用遍历的方法找到了最优值w,但是,通过遍历来寻找最最优值的方法效率未免有些低,所以我们引入梯度下降的方法来更新参数w。梯度是一个矢量,总指向当前点变化最快的方向。当该点为函数极值时,梯度为0。随机梯度下降法(SGD)公式为
w
=
w
?
l
r
?
(
d
y
/
d
x
)
\\w=w-lr*(dy/dx)
w=w?lr?(dy/dx)
由于有了梯度下降法,我们只需要给定一个w的初值,然后循环使用梯度下降法来更新参数,就能得到所需的最优w。
import numpy as np
import matplotlib.pyplot as plt
x_data=[1.0,2.0,3.0]##准备训练数据
y_data=[2.0,4.0,6.0]##测试
w=15 #随机给
def forward(x):##预测函数
return x*w##由于很明显所给数据符合wx,股不写b
def loss(x,y):##判断误差
Y_PRED=forward(x)
return (y-Y_PRED)**2
def gradi(x,y):#求梯度
return 2*x*(x*w-y)
epoch_list=[]
loss_list=[]
for epoch in range(30):
print("w=",w)
l_sum=0
for x_var,y_var in zip(x_data,y_data):
grad=gradi(x_var,y_var)
w=w-0.01*grad#梯度下降法
# print("\t grad:",x_var)
# print('\t',x_var,y_var,grad)
l=loss(x_var,y_var)
l_sum+=l
epoch_list.append(epoch)
loss_list.append(l_sum/3)
print('预测 4 对应的值是{}'.format(forward(4)))
plt.plot(epoch_list,loss_list)
plt.xlabel="训练次数"
plt.ylabel="损失值"
plt.show()
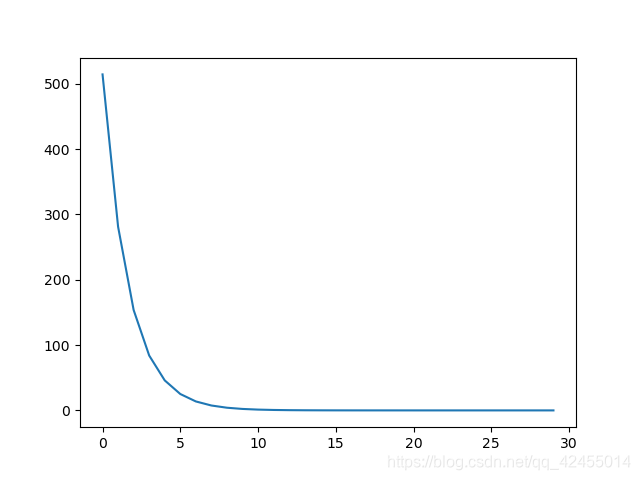
很明显,使用梯度下降法,损失值很快的收敛到了一个固定值。所以,梯度下降法十分有效
(3)、pytorch 实现梯度下降法求解回归问题
import torch
import numpy as np
import matplotlib.pyplot as plt
x=np.array(([1],[2],[3]))
y=torch.tensor(([4.0],[5.0],[6.0]))
x=torch.tensor(x,dtype=torch.float32)
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.liner=torch.nn.Linear(1,1)#建立一层线性层神经网络,线性层就是y=wx+b
def forward(self,x):
y_pred=self.liner(x)
return y_pred
model=Net()
critertion = torch.nn.MSELoss(size_average=False)##损失函数
optimizer=torch.optim.SGD(model.parameters(),lr=0.01)##优化器,使用了SGD
l_list=[]
e_list=[]
for epoch in range(10):
y_pred=model(x)
loss=critertion(y_pred,y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
l_list.append(loss.item())
e_list.append(epoch)
print("第{}次训练,损失是{}".format(epoch,loss.item()))
print("预测值15:{}".format(model(torch.tensor([[15.0]]))))
plt.plot(np.array(e_list),np.array(l_list))
plt.show()