[人工智能]学习曲线

学习曲线

学习曲线是诊断模型算法准确性的一个重要工具。

生成若干个在y=√x附近波动的点作为训练样本。

import numpy as np
import matplotlib.pyplot as plt
n_dots=200
X=np.linspace(0,1,n_dots)
Y=np.sqrt(X)+0.2*np.random.rand(n_dots)-0.1#[0,1]之间创建200个点
X=X.reshape(-1,1)
Y=Y.reshape(-1,1)

用pipline来处理数据

pipeline工作原理：

管道机制在机器学习算法中得以应用的根源在于，参数集在新数据集（比如测试集）上的重复使用。先增加多项式阶数，再用线性回归算法来拟合数据
逻辑原理如下：

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import  LinearRegression
def polynomial_model(degree=1):#degree表示多项式的阶数
    polynomial_features=PolynomialFeatures(degree=degree,include_bias=False)
    linear_regression=LinearRegression()#流水线，先增加多项式阶数，再用线性回归算法来拟合数据
    pipeline=Pipeline([("polynomial_features",polynomial_features),("linear_regression",linear_regression)])
    #流水线第一道工序：使用PolynomialFeatures来进行特征的构造，这里degree(多项式的度)为1。
    #流水线第二道工序：使用linear_regression线性回归类来拟合曲线。
    #最终返回
    return pipeline

polynmoial_model()用degree表示阶数来生成多项式模型

from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit
def plot_learning_curve(estimator,title,X,y,ylim=None,cv=None,n_jobs=1,train_sizes=np.linspace(.1,1.0,5)):
    #train_sizes=np.linspace(.1,1.0,5)表示把训练样本从0.1-1分成五等分序列，从序列中取出训练样本的数量百分比，逐个计算在当前训练样本数量情况下训练出来的样本准确性
    plt.title(title)
    if ylim is not None:
        plt.ylim(*ylim)
    plt.xlabel("Training examples")
    plt.ylabel("Score")
    train_sizes,train_scores,test_scores=learning_curve(estimator,X,y,cv=cv,n_jobs=n_jobs,train_sizes=train_sizes)

在sklearn里，我们不用自己实现学习曲线算法，直接使用sklearn.model_selection.learning_curve()函数来画学习曲线
X为传入的特征矩阵，y为传入标签
参数cv：
可以传多种格式参数：
（1）整数：指定KFold中的折数，如cv=5，意为将x特征矩阵分为5份，最终分数也会有5份
（2）None：默认为3折交叉验证
（3）分割器：例如ShuffleSplit(n_splits=50,test_size=0.2,random_state=0)
即按照传入分割器进行分割
参数n_jobs:
需要同时运行的CPU数，如果是-1，则调用所有CPU进行计算

    plt.title(title)
    train_scores_mean=np.mean(train_scores,axis=1)
    train_scores_std=np.std(train_scores,axis=1)#训练集的平均分，和中位数
    test_scores_mean = np.mean(test_scores, axis=1)
    test_scores_std = np.std(test_scores, axis=1)#测试集的平均分，和中位数
    plt.grid()
    plt.fill_between(train_sizes,train_scores_mean-train_scores_std,train_scores_mean+train_scores_std,alpha=0.1,color="r")
    plt.fill_between(train_sizes, test_scores_mean - test_scores_std, test_scores_mean + test_scores_std, alpha=0.1,
                     color="g")
    #plt.fill_between（）会把模型准确性的平均值的上下方差空间里用颜色填充
    plt.plot(train_sizes,train_scores_mean,'o--',color='r',label="Train scores")
    plt.plot(train_sizes, test_scores_mean, 'o-', color='g', label="Cross scores")
    plt.legend(loc="best")
    return plt

分别是使用polynmoial_model()构建出来的三个模型，分别为1阶，3阶，10阶多项式

cv=ShuffleSplit(n_splits=10,test_size=0.2,random_state=0)
plt.rcParams['font.sans-serif']=['simhei']   # 指定默认字体
titles=['学习曲线（欠拟合）','学习曲线','学习曲线（过拟合）']
degress=[1,3,10]
plt.figure(figsize=(18,4),dpi=200)
for i in range(len(degress)):
    plt.subplot(1,3,i+1)
    plot_learning_curve(polynomial_model(degress[i]),titles[i],X,Y,ylim=(0.75,1.01),cv=cv)
plt.show()

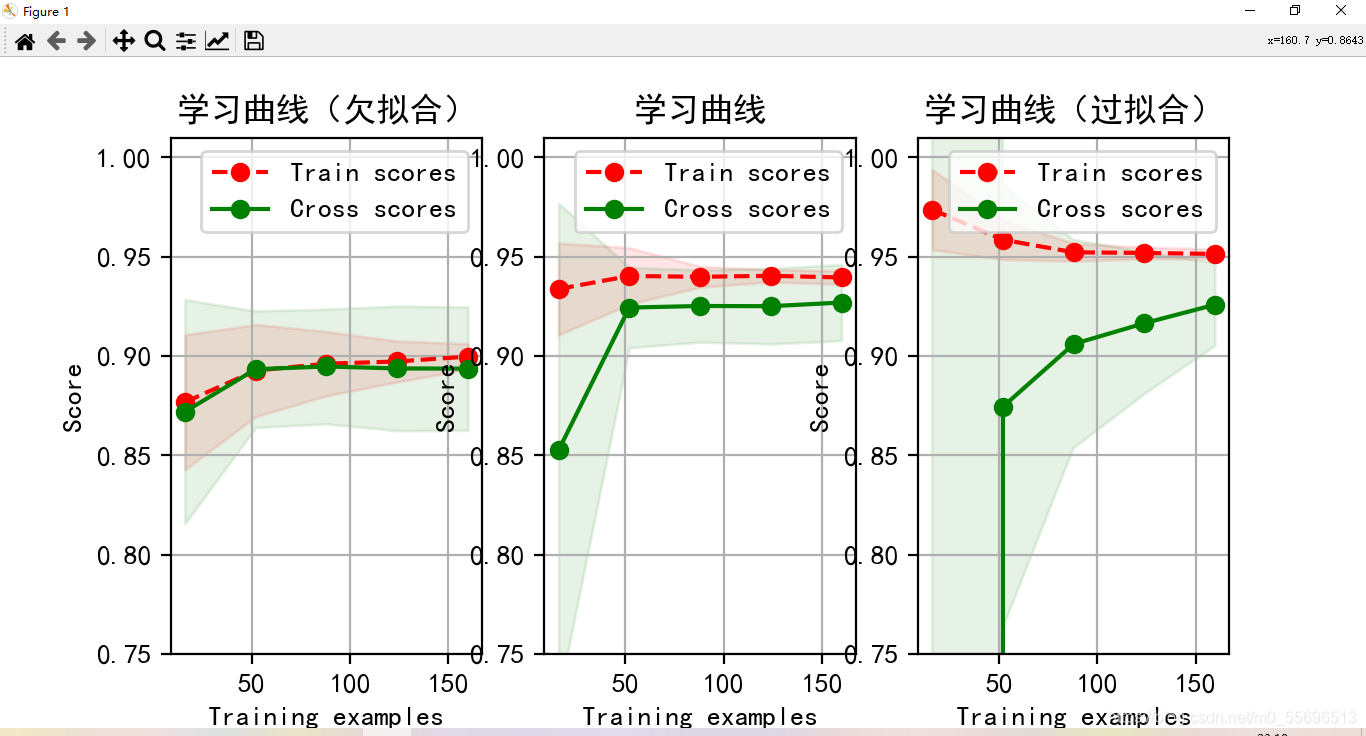
当模型欠拟合时，随着训练数据集的增加，交叉数据集的准确性（实线）逐渐增大，逐渐和训练集的准确性（虚线）靠近，但其总体水平比较低，收敛在0.88左右。其训练数据集的准确性也比较低，收敛在0.90左右。
当模型过拟合时，随着训练数据集的增加，交叉数据集的准确性（实线）也逐渐增大，逐渐和训练集的准确性（虚线）靠近，但两者之间的间隙较大，训练集的准确性很高，收敛在0.95左右。但其交叉验证数据集的准确性值却很低，收敛在0.91左右。

过拟合与欠拟合的特征：

过拟合：模型对训练数据集的准确性比较高，其成本$J_{train}(\theta )$比较低，对交叉验证数据集的准确性较低，其成本$J_{cv}(\theta )$比较高。
欠拟合：模型对训练数据集的准确性比较低，其成本$J_{train}(\theta )$比较高，对交叉验证数据集的准确性较低，其成本$J_{cv}(\theta )$比较高。