[人工智能]李宏毅机器学习课程梳理【十三】：Semi-supervised & Unsupervised Learning

摘要

半监督学习相较于监督学习，既保留标记数据用以模型训练，又大幅度增加数据的数量，未标记数据可以提高参数的准确性。半监督学习可以应用在全部类型的监督学习上，重新定义加入未标记数据后的计算过程，但不改变算法本身的原理与特点，文章将半监督学习融入Generative Model中，更改算法，观察其仍为Soft Label分类方法。半监督学习在实践中往往需要“假设”，“假设”的合理性决定结果的准确性，算法应用“假设”制定计算过程或判定标准。无监督学习适合解决自然语言处理问题。

1 基本概念

监督学习的训练集数据是 { ( x r , y ^ r ) } r = 1 R \{(x^r,\hat y^r)\}^R_{r=1} {(xr,y^?r)}r=1R?，半监督学习的训练集数据是少量 { ( x r , y ^ r ) } r = 1 R \{(x^r,\hat y^r)\}^R_{r=1} {(xr,y^?r)}r=1R?和大量 { x u } u = R R + U \{x^u\}_{u=R}^{R+U} {xu}u=RR+U?
半监督学习分为两类，Transductive learning与Inductive learning，前者使用testing set的feature，前者的未标记的数据是testing data。

可以使用testing set的feature，不可以使用testing set的label

Semi-supervised Learning在区分unlabeled data时往往依照某些假设，所以假设的合理性会很大程度上影响结果的准确性。

2 Semi-supervised Learning for Generative Model

未标记的数据可以提高$P(C_1),P(C_2),{\mu }^1,{\mu }^2,\Sigma$等参数的准确性。

下面介绍Semi-supervised Generative Model的计算步骤。记 $\theta$ 为所有参数，
step1：计算每一笔未标记数据$x^u$的后验概率$P_{\theta }(C_1|x^u)$，得到未标记数据属于class1的概率
step2：更新Model，记$N$为数据总数量，$N_1$为有标记数据中属于class1的数量，$P(C_1)=\frac{N_1+{\sum }_{x^u}P(C_1|x^u)}{N}$，${\mu }^1=\frac{1}{N}\sum _{x^r\in C_1}{x}^r+\frac{1}{{\sum }_{x^u}P(C_1|x^u)}\sum _{x^u}P(C_1|x^u)x^u$
step3：重复step1【有了新Model后概率会变化】
step4：重复step2

上述算法的计算原理：
计算标记数据与未标记数据和的maximum likelihood，$logL(\theta )=\sum _{x^r}log{P}_{\theta }(x^u,{\hat{y}}^r)+\sum _{x^u}log{P}_{\theta }(x^u)$，其中$P_{\theta }(x^r,{\hat{y}}^r)=P_{\theta }(x^r|{\hat{y}}^r)P({\hat{y}}^r),P_{\theta }(x^u)=P_{\theta }(x^u|C_1)P(C_1)+P_{\theta }(x^u|C_2)P(C_2)$，而上述算法每更新一次Model，$logL(\theta )$增大，最终收敛。

3 Low-density Separation Assumption

是一个常用假设，营造一个非黑即白的世界，假设两个class之间会有一个低密度的分界线。
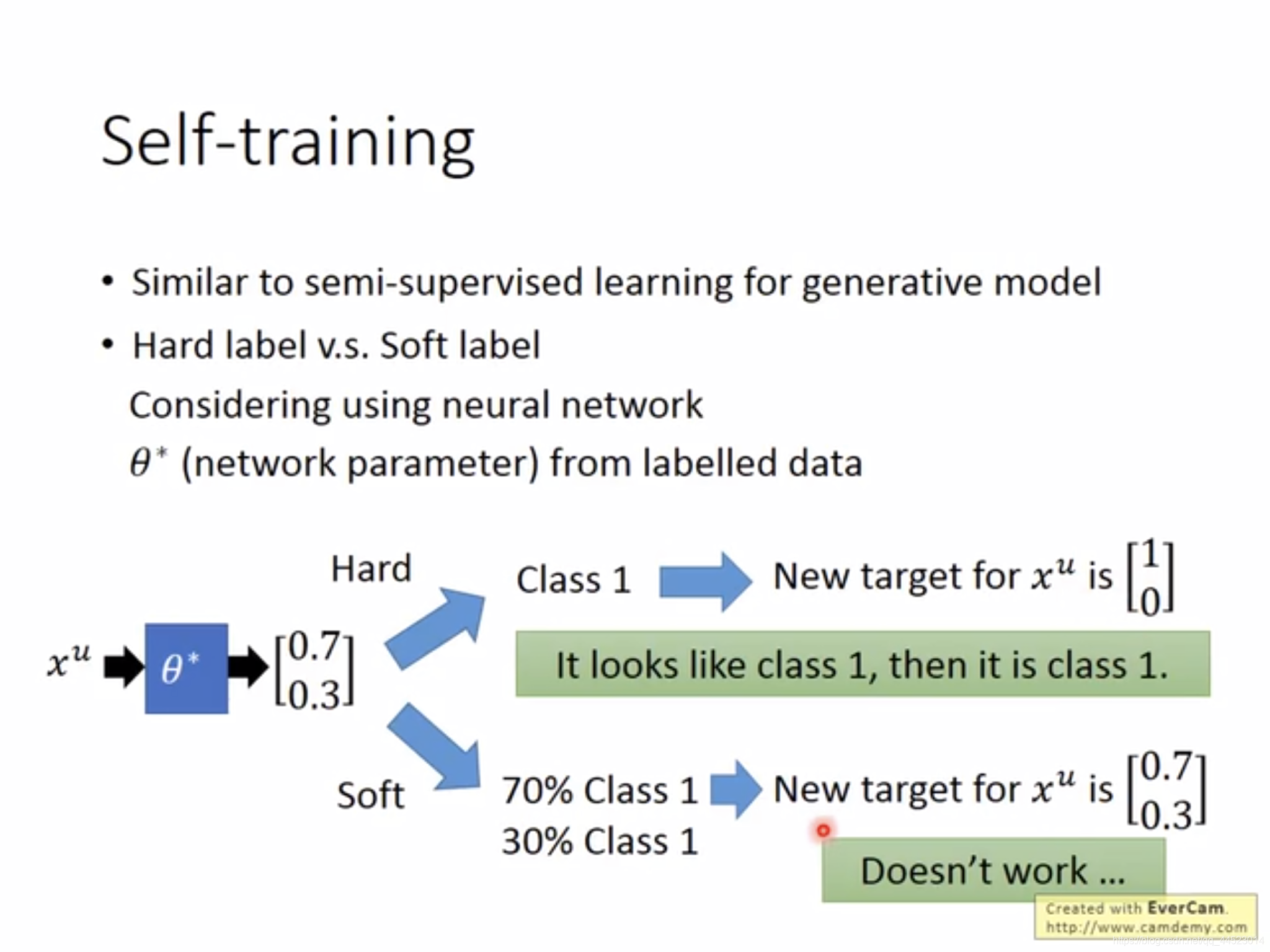
Low-density Separation Assumption最具代表性的方法是Self-training，给定一些标记数据与未标记数据，第一步根据标记数据训练一个模型$f^{?}$，第二步Pseudo-label用$f^{?}$给未标记数据分类，第三步从未标记数据集中拿出一部分data，【如何拿出的算法需要自己设计】，加入到标记数据集中。于是标记数据集改变，重复上述三个步骤。

在使用Neural Network时，算法要使用Hard label，这样能体现把“权重”变为“非黑即白”的效果，会有较好表现

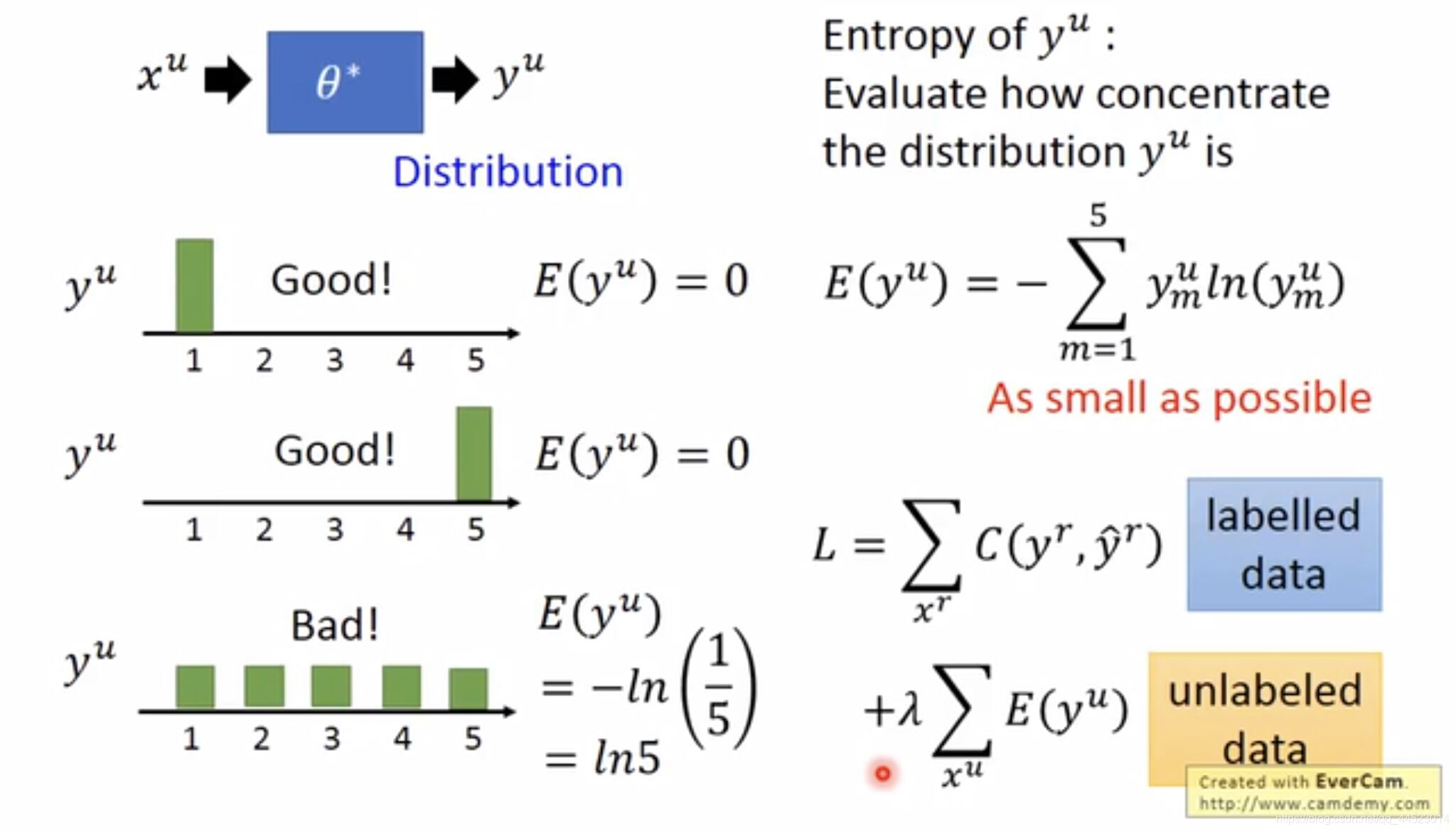
Low-density Separation Assumption另一个代表方法是Entropy-based Regularization，增加一项“用数字的方法定义分类结果的好坏”，即用一个值来表示这个Model的概率分布是集中还是分散。在图2的例子中，这一项为$E(y^u)=?\sum _{m=1}^5{y}_m^{u}ln(y_m^u)$，希望在unlabel data上entropy越小越好。Loss function为$L=\sum _{x^r}C(y^r,{\hat{y}}^r)+\lambda \sum _{x^u}E(y^u)$，这样减小过拟合的可能。

4 Smoothness Assumption

另一个常用的假设，指x的分布是不平均的，它在一些地方很集中，一些地方很分散；如果$x^1,x^2$可以在高密度的地方距离较近，那么${\hat{y}}^1,{\hat{y}}^2$的结果相似。可以理解成$x^1,x^2$可以有一条数据高密度的路径相连，那么两者的结果很像。
实践Smoothness Assumption的方法一：Cluster and then Label。画出数据的概率分布图，就可以很直观地根据密集度做聚类分析。但问题是仅根据像素做聚类分析不太准，如果想有效，需要deep auto-encoder做特征变换再聚类分析。
实践Smoothness Assumption的方法二：Graph-based Approach。引入图结构来表达“高密度的路径”。将所有的data point建成一张图，能通过节点连接上的可以看作一个class，如图3所示。

如何建Graph？
第一步，定义$x^i,x^j$之间的相似度$s(x^i,x^j)$，比如基于auto-encoder抽出的feature算相似度、采用Gaussian Radial Basis Function：$s(x^i,x^j)=exp(?\gamma ||x^i?x^j|{|}^2)$，【用指数可使距离稍远的点相似度下降很快】
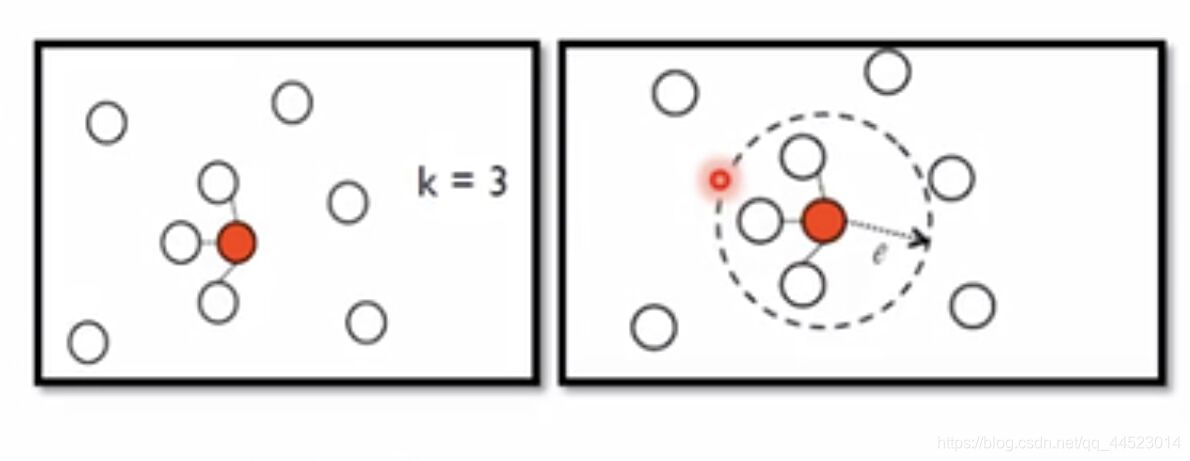
第二步，添加edge，可以做出几类图，如K Nearest Neighbor、e-Neighborhood(相似度大于e者连起来)

第三步，给edge赋权值，权值与连接的两个data points之间的相似度$s(x^i,x^j)$成正比。
具体计算如下：
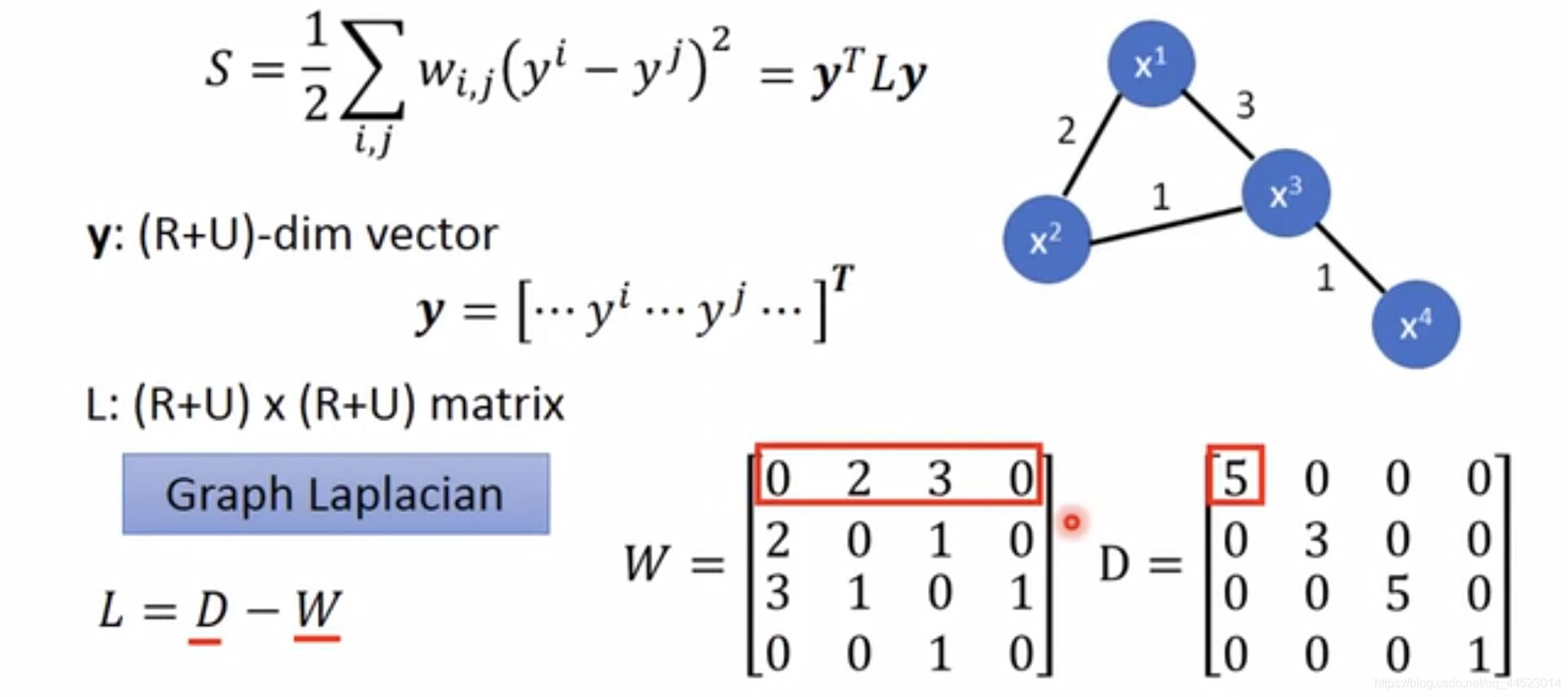
在图结构上面定义the smoothness of the labels：$S=\frac{1}{2}\sum _{i,j}{w}_{i,j}(y^i?y^j{)}^2$，这个求和是对所有数据(R+U)，无论是否标记。S越小越好。下图给出更简便的计算过程，W填入权值，为对称阵；D为对角阵。

Loss function：$L=\sum _{x^r}C(y^r,{\hat{y}}^r)+\lambda S$

5 总结与展望

半监督学习与无监督学习的未标记数据较容易获取，通过改变算法，如加入图结构等方法将其利用，提高结果的准确性。半监督学习常用的Low-density Separation Assumption与Smoothness Assumption假设，为未标记数据的区分划定标准，并给出了实践算法的定性分析与定量计算。