[人工智能]机器学习实战第五章

Logistic回归

• 说明：本章节所有代码使用版本为Python3

优点：计算代价不高，易于理解和实现
缺点：容易欠拟合，分类精度可能不高
适用数据类型：数值型和标称型数据

??这是最优化算法。主要思想是：根据现有的数据对分类边界线建立回归公式，以此进行分类。“ 回归 ”一词源于最佳拟合，表示要找到最佳拟合参数集。训练分类器识的做法就是寻找最佳拟合参数。

Logistic回归的一般过程

1. 收集数据：采用任意方法收集数据
2. 准备数据：由于需要进行距离计算，因此要求数据类型为数值型。另外，结构化数据格式则最佳
3. 分析数据：采用任意方法对数据进行分析
4. 训练算法：计算不同独立特征的条件概率
5. 测试算法：一旦训练步骤完成，分类将会很快
6. 使用算法：首先需要输入一些数据，并将其转化成对应的结构化数值；接着，基于训练好的的回归系数就可以对这些数值进行简单的回归计算，判定他们属于哪个类别；之后就可以在输出的类别上做出一些其他的分析工作。

基于Logistic回归和Sigmoid函数的分类

??我们想要的函数，能接受所有的输入然后预测出类别。Sigmoid函数具有输出0或1的这种性质，而且在数学上容易处理。因此为了实现Logistic回归分类器，我们可以在每一个特征上都乘以一个回归系统，然后将所有的结果值相加，将这个总和代入Sigmoid函数中，进而得到一个范围在0~1之间的数值。Sigmoid函数定义：

$$\sigma (z)=\frac{1}{1+e^{?z}}$$

任何大于0.5的数据被分入1类，小于0.5的数据被归入0类。所以Logistic回归也可以看成是一种概率估计。

基于最优化方法的最佳回归系数确定

??Sigmoid函数的输入记为z，公式为：

$$z=w_0{x}_0+w_1{x}_1+w_2{x}_2+...+w_n{x}_n$$

上述公式可简化为$z=W^{T}x$，它表示数值向量对应元素相乘然后全部相加起来即得到$z$值。其中的向量$x$是分类器的输入数据，向量$w$是要求的最佳参数（系数），使分类器尽可能的精确。

梯度上升法

??思想：要找到某函数的最大值，最好的方法是沿着该函数的梯度方向探寻。函数$f(x,y)$的表示：

$$?f(x,y)=?\begin{array}{c}\frac{?f(x,y)}{?x}\\ \frac{?f(x,y)}{?y}\end{array}?$$

要记住这些符号的含义：这个梯度意味着要沿$x$的方向移动$\frac{?f(x,y)}{?x}$，沿$y$的方向移动$\frac{?f(x,y)}{?y}$。其中，函数$f(x,y)$必须要在待计算的点上有定义并且可微。
??梯度算子总是指向函数值增长最快的方向。这里说的是移动方向，而没有提到移动量的大小。该量值称为步长，记作$a$。用向量来表示梯度上升算法：

$$w:=w+a{?}_{w}f(w)$$

??该公式将一直被迭代执行，直到达到某一停止条件为止。

??我们最经常听到梯度下降算法，它与梯度上升算法是一样的，只是公式中加法变成减法。因此，公式为：
$$w:=w?a{?}_{w}f(w)$$
??梯度上升算法用来求函数的最大值，而梯度下降算法用来求函数的最小值。

训练算法：使用梯度上升找到最佳参数

??通过梯度上升找到最佳参数，也就是拟合出Logistic回归模型的最佳参数。

分析数据：画出决策边界

??从上面已经解出了一组回归系数，他确定了不同类别数据之间的分割线。

训练算法：随机梯度上升

??梯度上升算法在每次更新回归系数的时候需要遍历整个数据集，该方法在处理100个左右的数据的时候还可以，但若有数十亿样本和成千上万的特征，该方法复杂度就太高了，一种改进的方法是一次仅使用一个样本点来更新回归系数，该方法称为随机梯度上升算法。由于可以在新样本到来时对分类器进行增量式更新，因而随机梯度上升算法是一个在线学习算法。

5、完整示例代码

from numpy import mat, shape, ones
import numpy as np
import matplotlib.pyplot as plt
from numpy.core.records import array

# 加载数据集
def loadDataSet():
    dataMat = []
    # 数据
    labelMat = []
    # 数据的标签
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        # strip()将每一行数据按照换行符来分割，split()按照\t来切割
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        # 向dataMat中追加数据，分别是1.0，读取到的第一列数据和第二列数据
        # lineArr[0]与lineArr[1]是每一组数据的两个特征
        labelMat.append(int(lineArr[2]))
        # 将testSet.txt文件中的最后一列数据添加到labelMat中
    return dataMat, labelMat

# sigmoid函数的计算方式
def sigmoid(inX):
    return 1.0 / (1.0 + np.exp(-inX))
    # 计算方法：1/(1+e^(-z))

# 梯度上升算法
def gradAscent(dataMatIn, classLabels):
    dataMatrix = mat(dataMatIn)
    # mat()用来创建矩阵，将dataMatIn数组转化成矩阵100*3
    lableMat = mat(classLabels).transpose()
    # 将classLabels数组转化成二维的矩阵，此处为一个行向量，.transpose()将其转化成列向量
    m, n = shape(dataMatIn)
    # shape() 获取dataMatIn的行数与列数100*3
    alpha = 0.001
    # 学习率
    maxCycles = 500
    # 迭代次数
    weights = ones((n, 1))
    # 创建一个列向量3*1
    for k in range(maxCycles):
        h = sigmoid(dataMatrix*weights)
        # h是一个列向量，因为weights就是一个列向量，这里的dataMatrix是100*3，weights是3*1
        # 所以最终得到的是100*1的数据（列向量）传给sigmoid，相应的sigmoid返回也是列向量
        error = (lableMat - h)
        # lableMat与h之间的差值是误差
        weights = weights + alpha * dataMatrix.transpose() * error
        # 参考https://blog.csdn.net/kaka19880812/article/details/46993917
        # 根据w:=w+af(w)来计算的，更新参数数值
    return weights

# 画出数据集与Logistics回归最佳拟合直线的函数
def plotBestFit(weights):
    dataMat, labelMat = loadDataSet()
    # 加载数据集
    dataArr = np.array(dataMat)
    # 将数据集变成数组，此处为100*3的数组
    n = shape(dataArr)[0]
    # n为数组的行数
    xcord1 = []
    ycord1 = []
    xcord2 = []
    ycord2 = []
    for i in range(n):
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i, 1])
            # 标签为 1 的数据的第一个特征追加到xcord1
            ycord1.append(dataArr[i, 2])
            # 标签为 1 的数据的第二个特征追加到ycord1
        else:
            xcord2.append(dataArr[i, 1])
            # 标签为 0 的数据的第一个特征追加到xcord2
            ycord2.append(dataArr[i, 2])
            # 标签为 0 的数据的第二个特征追加到ycord2
    fig = plt.figure()
    # 新建figure对象
    ax = fig.add_subplot(111)
    # 新建子图1，子图格式1行1列第一个图
    ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
    # scatter前两个参数(x,y)设置点的位置，第三个参数设置点的大小，第四个点设置点的颜色
    ax.scatter(xcord2, ycord2, s=30, c='green')
    x = np.arange(-3.0, 3.0, 0.1)
    # 设置 x 轴的取值范围，并设步长为0.1
    y = (-weights[0]-weights[1]*x)/weights[2]
    # 最佳拟合直线
    ax.plot(x, y)
    plt.xlabel('X1')
    plt.ylabel('X2')
    # x，y的标题
    plt.show()

# 随机梯度上升算法
def stocGradAscent0(dataMatrix, classLabels):
    m, n = shape(dataMatrix)
    # 获取数据集的行列数m，n
    dataMatrix = np.array(dataMatrix)
    # 这一行代码是为了解决：TypeError: can't multiply sequence by non-int of type 'float'
    # 笔者在实现的时候，一直报这个错误，差一些以文章还是没有答案，最后在一篇博文中找到了解决办法
    # 原文是：https://blog.csdn.net/qq_43149373/article/details/89790153
    alpha = 0.01
    # 学习率
    weights = np.ones(n)
    # 创建一个 1行，n列的矩阵
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i]*weights))
        # 与梯度上升算法不同，随机梯度上升算法h与error都是数值
        # sum(dataMatrix[i]*weights)将所有的特征，都转化成了一个数值
        error = classLabels[i]-h
        # 真正的标签值与预测的误差
        weights = weights+alpha*error*dataMatrix[i]
        # 更新回归系数
    return weights

# 改进随机梯度上升算法
def stocGradAscent1(dataMatrix, classLabels,numIter=150):
    m, n = shape(dataMatrix)
    # 获取数据集的行列数m，n
    dataMatrix = np.array(dataMatrix)
    # 这一行代码是为了解决：TypeError: can't multiply sequence by non-int of type 'float'
    # 笔者在实现的时候，一直报这个错误，查了一些以文章还是没有答案，最后在一篇博文中找到了解决办法
    # 原文是：https://blog.csdn.net/qq_43149373/article/details/89790153
    weights = np.ones(n)
    # 创建一个 1行，n列的矩阵
    for j in range(numIter):
        dataIndex=list(range(m))
        # 笔者在实现代码的时候发现dataIndex=range(m)报错：TypeError: 'range' object doesn't support item deletion
        # 根据上一个的教训，直接变成list，可以实现删除，则强转为list类型
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.01
            # 学习率，每次迭代都会进行调整
            randIndex=int(np.random.uniform(0,len(dataIndex)))
            # 随机选取更新，从一个均匀分布[low,high)中随机采样，注意定义域是左闭右开，即包含low，不包含high
            h = sigmoid(sum(dataMatrix[randIndex]*weights))
            # 与梯度上升算法不同，改进的随机梯度上升算法h与error都是数值
            # sum(dataMatrix[randIndex]*weights)将所有的特征，都转化成了一个数值
            error = classLabels[randIndex]-h
            # 真正的标签值与预测的误差
            weights = weights+alpha*error*dataMatrix[randIndex]
            # 更新回归系数
            del(dataIndex[randIndex])
            # 选用过后的数据要删除，避免重复使用
    return weights

dataMatIn, classLabels = loadDataSet()
weights = stocGradAscent1(dataMatIn, classLabels)
# 改进之后的梯度上升算法
weights = stocGradAscent0(dataMatIn, classLabels)
# 改进之前的梯度上升算法
plotBestFit(weights)
# plotBestFit(weights.getA())
# getA()或mat.A ,matrix矩阵名.A 代表将矩阵转化为array数组类型
# 这个是梯度上升算法使用时调用的

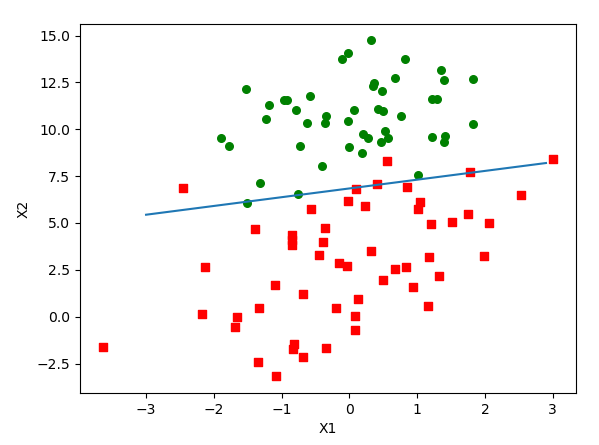
$$梯度上升算法结果$$
$$随机梯度上升算法结果$$

$$改进随机梯度上升算法结果$$

??从结果上看，梯度上升算法比改进前的梯度上升算法要好。因为改进前的梯度上升算法分类器错分了近一半的样本，但是直接看结果是不公平的。梯度上升算法在整个数据集上迭代了500次，才将结果收敛达到了稳定值，而改进前的梯度上升算法在整个数据集上迭代了200次达到了最终的效果。
??改进后的程序，通过随机选取样本来更新回归系数，这种方法将减少周期性的波动，而且增加了一个迭代次数作为第三个参数。

示例从疝气病症预测病马的死亡率

使用Logistic回归估计马疝病的死亡率

1. 收集数据：给定数据文件
2. 准备数据：用python解析文本文件并填充缺失值
3. 分析数据：可视化并观察数据
4. 训练算法：使用优化算法，找到最佳的系数
5. 测试算法：为了量化回归的效果，需要观察错误率。根据错误率决定是否回退到训练阶段，通过改变迭代的次数与步长等参数来得到更好的回归系数
6. 使用算法：实现一个简单的命令行程序来收集马的症状并输出预测的结果

1、准备数据：处理数据中的缺失值

??解决缺失数据的一些可选办法：

• 使用可用特征的均值来填补缺失值
• 使用特殊值来填补缺失值，如-1
• 忽略有缺失值的样本
• 使用相似样本的均值添补缺失值
• 使用另外的机器学习算法预测缺失值

??在预处理阶段需要做的事：

1. 所有的缺失值必须有一个实数来替换，因为numpy数据类型不允许包含缺失值
2. 若在测试数据中发现了一条数据类别的标签已经有缺失，则最简单的方式是直接丢弃该数据

2、测试算法：用Logistic回归进行分类

??将数据上的每一个特征向量乘以最优化方法得来的回归系数，再将该乘积结果求和，最后输入到Sigmoid函数中即可

3、完整示例代码

import numpy as np
from numpy import *

# 以回归系数与特征向量作为输入来计算对应Sigmoid值
def classifyVector(inX,weights):
    prob=sigmoid(sum(inX*weights))
    # 求Sigmoid值
    if prob>0.5:  return 1.0
    else: return 0.0
    # 要是Sigmoid值大于0.5则返回 1 ，否则返回 0 

# 对数据进行格式化处理，并计算错误率
def colicTset():
    frTrain=open('./horseColicTraining.txt')
    # 读取训练数据
    frTest=open('./horseColicTest.txt')
    # 读取测试数据
    trainingSet=[]
    trainingLabels=[]
    for line in frTrain.readlines():
        currLine=line.strip().split('\t')
        # strip()将每一行数据按照换行符来分割，split()按照\t来切割，形成数组
        lineArr=[]
        for i in range(21):
            lineArr.append(float(currLine[i]))
            # 获取前20列的数据，保存到lineArr中，这是训练数据
        trainingSet.append(lineArr)
        # 训练数据放到trainingSet中
        trainingLabels.append(float(currLine[21]))
        # 最后一列是标签，将标签数据放到trainingSet中
    trainWeights=stocGradAscent1(array(trainingSet),trainingLabels,500)
    # 使用改进随机梯度上升算法，迭代次数500，求回归向量系数
    errorCount=0
    numTestVec=0.0
    for line in frTest.readlines():
        numTestVec+=1.0
        # 测试数据个数
        currLine=line.strip().split('\t')
        # strip()将每一行数据按照换行符来分割，split()按照\t来切割，形成数组
        lineArr=[]
        for i in range(21):
            lineArr.append(float(currLine[i]))
            # 获取前20列的数据，保存到lineArr中，这是当前一行数据的所有值
        if int(classifyVector(array(lineArr),trainWeights))!=int(currLine[21]):
            # classifyVector返回对应Sigmoid值， 0 或者 1 ，与测试属于比较，要是预测与实际不相同证明预测是错误的
            errorCount+=1
    errorRate=(float(errorCount)/numTestVec)
    # 错误率是预测错误个数除以测试数据个数
    print("The error rate of this test is %f"%errorRate)
    return errorRate
    # 返回错误率

def multiTest():
    numTest=10
    # 选用10次进行测试
    errorSum=0.0
    for k in range(numTest):
        errorSum+=colicTset()
    # 10次测试求平均值
    print("After %d iterations the average error rate is: %f"%(numTest,errorSum/float(numTest)))


# sigmoid函数的计算方式
def sigmoid(inX):
    # return 1.0 / (1.0 + np.exp(-inX))
    # 计算方法：1/(1+e^(-z))
    # 在运行的时候报错了：RuntimeWarning: overflow encountered in exp
    # 网上的解释是：https://blog.csdn.net/CY_TEC/article/details/106083366
    if inX>=0:
    # 对sigmoid函数的优化，避免了出现极大的数据溢出
        return 1.0/(1+np.exp(-inX))
    else:
        return np.exp(inX)/(1+np.exp(inX))

# 改进随机梯度上升算法
def stocGradAscent1(dataMatrix, classLabels,numIter=150):
    m, n = shape(dataMatrix)
    # 获取数据集的行列数m，n
    dataMatrix = np.array(dataMatrix)
    # 这一行代码是为了解决：TypeError: can't multiply sequence by non-int of type 'float'
    # 笔者在实现的时候，一直报这个错误，查了一些以文章还是没有答案，最后在一篇博文中找到了解决办法
    # 原文是：https://blog.csdn.net/qq_43149373/article/details/89790153
    weights = np.ones(n)
    # 创建一个 1行，n列的矩阵
    for j in range(numIter):
        dataIndex=list(range(m))
        # 笔者在实现代码的时候发现dataIndex=range(m)报错：TypeError: 'range' object doesn't support item deletion
        # 根据上一个的教训，直接变成list，可以实现删除，则强转为list类型
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.01
            # 学习率，每次迭代都会进行调整
            randIndex=int(np.random.uniform(0,len(dataIndex)))
            # 随机选取更新，从一个均匀分布[low,high)中随机采样，注意定义域是左闭右开，即包含low，不包含high
            h = sigmoid(sum(dataMatrix[randIndex]*weights))
            # 与梯度上升算法不同，改进的随机梯度上升算法h与error都是数值
            # sum(dataMatrix[randIndex]*weights)将所有的特征，都转化成了一个数值
            error = classLabels[randIndex]-h
            # 真正的标签值与预测的误差
            weights = weights+alpha*error*dataMatrix[randIndex]
            # 更新回归系数
            del(dataIndex[randIndex])
            # 选用过后的数据要删除，避免重复使用
    return weights

multiTest()

小结

??Logistic回归的目的是寻找一个非线性的函数Sigmoid的最佳拟合参数，求解过程可以是最优化算法来完成。在最优化算法中，最常用的是梯度上升算法，而梯度上升算法又可以简化为随机梯度上升算法。
??随机梯度上升算法与梯度上升算法效果相当，但是占用资源较少。此外随机梯度上升是一个线性算法，它可以在新数据到来时就完成参数更新，而不需要重新读取整个数据集来进行批处理运算。
??机器学习的一个重要问题就是处理缺失数据，解决的方法取决于实际应用的需求。

由于代码中horseColicTraining.txt与horseColicTest.txt文件数据较多，请读者自行查找数据