图上的传统机器学习方法
一. Tradtion Feature-based Methods Node

传统机器学习方法,我们希望训练一个模型,在给定一个新节点,新链接或图的情况能够获取它的特征并做出预测。


在图的特征提取过程,我们将它转化成一个d维的向量,特征对象可以是节点,边,完整的图,节点集。这里我们考虑的图为无向图。
所以我们要解决的问题就是在给定 G=(V,E),如何学习节点V的特征来学习目标函数。
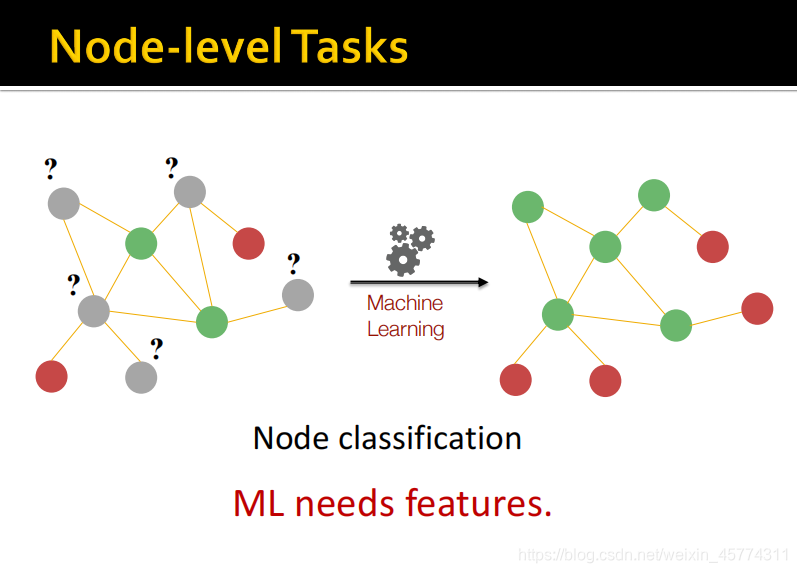
首先我们考虑节点水平上的任务,如上图所示做一个节点分类,我们希望从左图中学习到一些东西进而预测节点类别来得到右图。这些东西就是节点的特征。观察上图可知,红色节点只有一条边相连,绿色节点有多条边相连,即红色节点的度为1,绿色节点的度大于1,根据节点的度这个特征,我们就可以做出一个简单的分类。
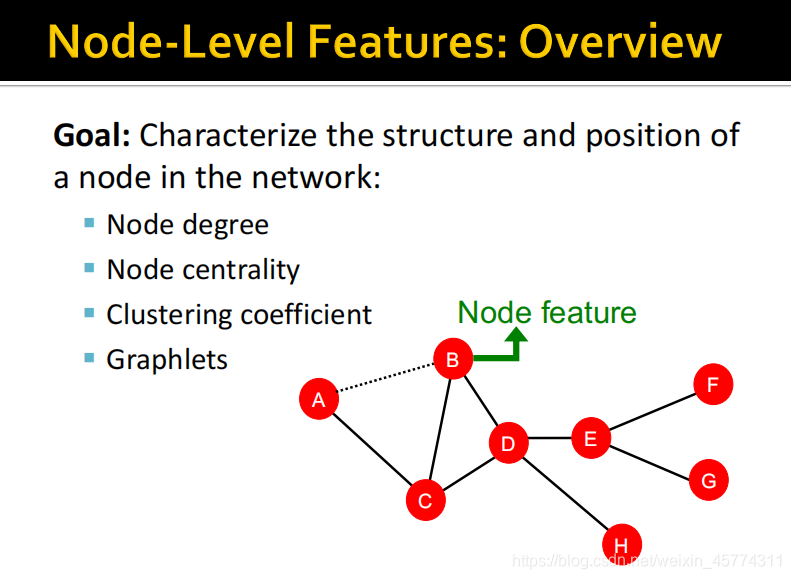
一般有这4种常见的节点特征:
1.节点度
2.节点中心性
3.局部聚集系数
4.图元
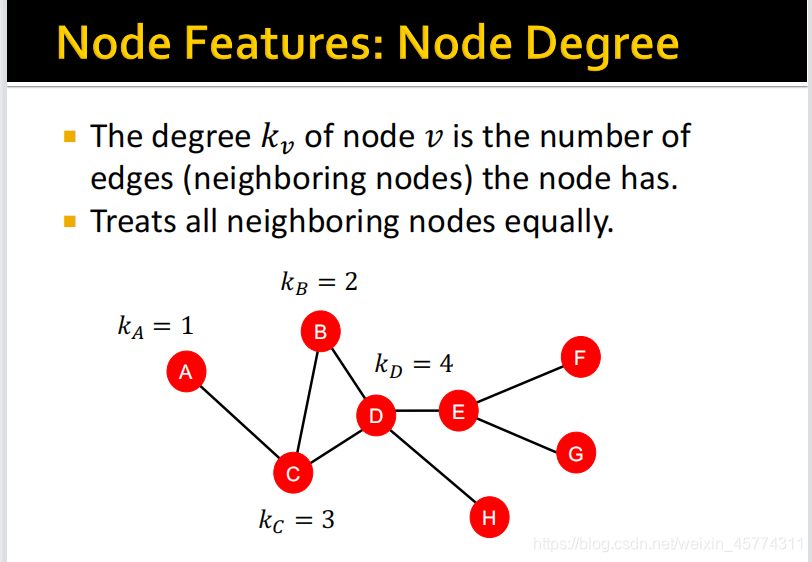
但是节点度有一个缺点,当两个节点的度相同时,模型会认为是相同的特征,而不会考虑节点在图中的位置关系和节点的重要性,节点度只考虑节点邻居节点的数量。

节点中心性考虑到图中的节点的重要性,根据不同方式有以下三种:
1.特征向量中心性
2.中介中心性
3.紧密中心性


上述方程以递归形式计算,转化成矩阵形式可以看出,所求即为特征向量,该邻接矩阵中,若两节点之间有边,则为1
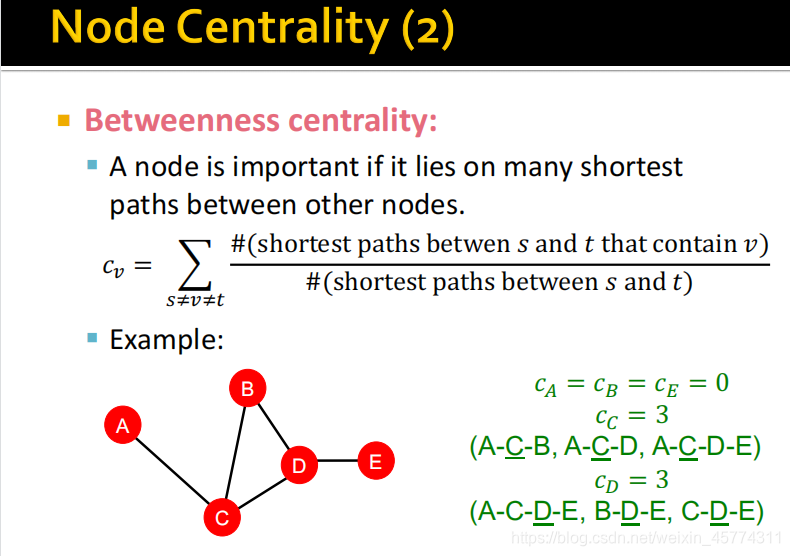
第二种是中介中心性,定义为一个节点位于其他节点之间的许多最短路径上,说明它具有重要性。如图,对节点 A, B, E来说,A,E不是任何路径的中间节点,B是路径 C-B-D的中间节点,但是该路径不是最短路径,所以都为0。对于C存在以上所示3条最短路径,Cv=1/1+1/1+1/1=3。因为在上述例子中节点之间的最短路径为1,所以分母为1。

紧密中心性,定义为如果一个节点对所有其他节点的最短路径长度都很小,说明具有重要性。上述公式分母为该节点为起始的最短路径的长度和。

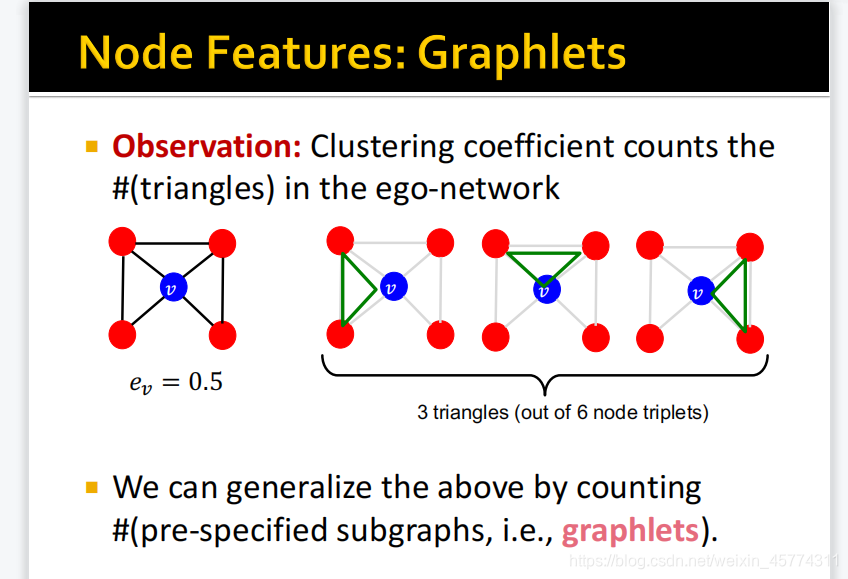
局部聚集系数,分子为邻居节点之间构成的边数量,分母为邻居节点所能构成的最大边数量。以图2为了,邻居节点之间构成3条边,4个邻居节点所能构成最大边数量为6,所以聚集系数为0.5。聚集系数越大代表该节点所处位置更密集,更接近图网络中心。

图元:有根连接的非同构子图。如上图3个节点的图元,3节点链式的有2种情况,三角形只有一种,因为其他位置是同构的。

GDV: 一个图元度向量是以该给定节点为根的图元的计数向量

图元度向量的计算:对于示例给定的图,我们使用三种图元,共4种情况(a,b,c,d),也是GDV的长度。考虑节点v:
a:2种位置情况
b:一种
c:与b同构,不重复计算
d:2中位置情况
所以节点v的GDV为 [2, 1, 0, 2]

1. 考虑2-5个节点的图元可以得到73种结构。最多获取其相互连接到4跳的距离,对于5个节点,一个节点到另一个节点的最长链路为4。
2. 图元度向量提供了一个节点的局部网络拓扑的度量:提供了比节点度或聚类系数更详细的局部拓扑相似性的度量。

基于节点重要性的特征可用于预测图中有影响的节点,如预测社交网络中的名人用户。

基于结构的特征可用于预测节点在图中扮演的特定角色,如预测蛋白质-蛋白质相互作用网络中的蛋白质功能。