[人工智能]梯度下降法可视化

一、机器学习

机器学习用一句话概括就是“根据数据找函数”。具体相关内容可以访问链接 https://www.cnblogs.com/subconscious/p/4107357.html ，个人觉得讲的通俗易懂，适合新手和初级玩家。

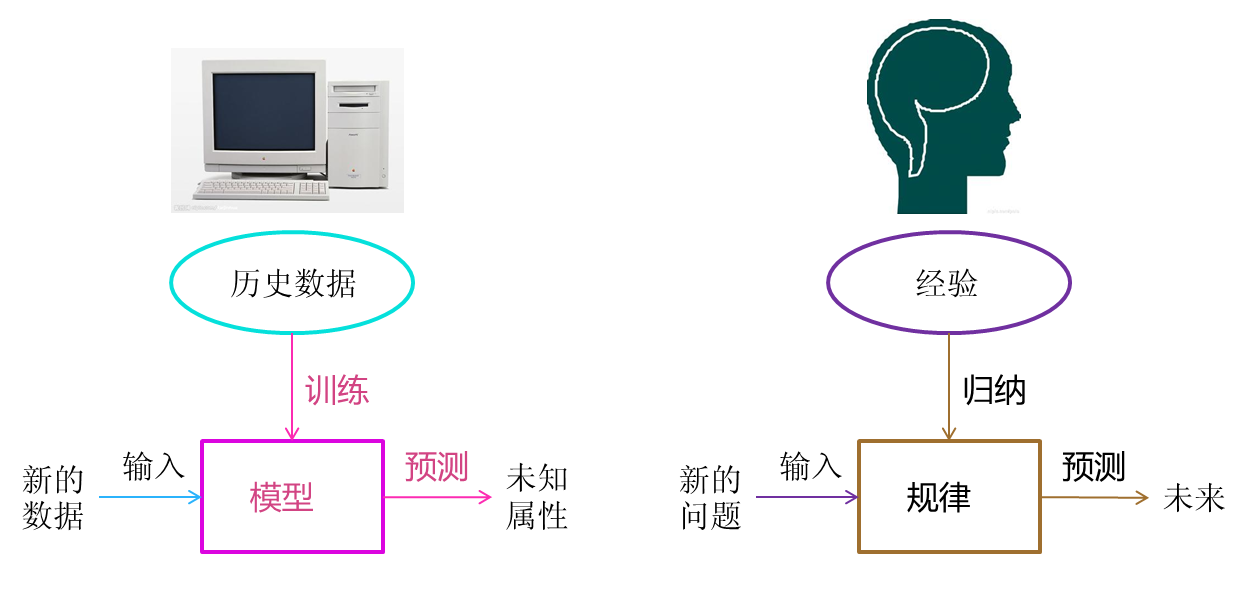
举个例子，假设女生择偶时主要根据“高富帅”来决定是否要在一起，那么先通过采访或者问卷调查得到一大批数据样本，每个样本为不同女生的择偶标准，这时我们就可以对这些样本进行统计分析，找出通用的规律，我们可以将其表示为：

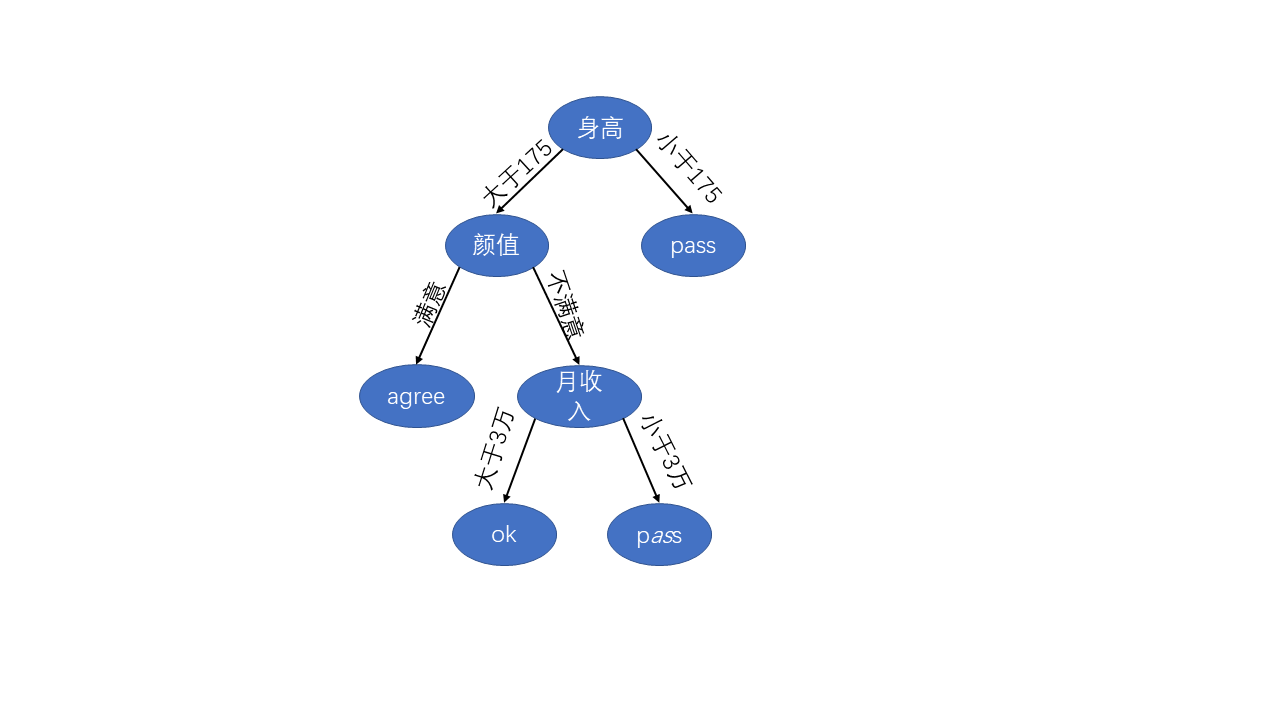
这样我们男生就可以知道绝大数女性择偶标准了，可以将自己的情况输入到这棵决策树中，看看自己是“pass"还是”ok"。此处建议：如果身高没希望了，就整整颜值，如果这两个都没希望，那么就好好提高自己的能力，提高收入。

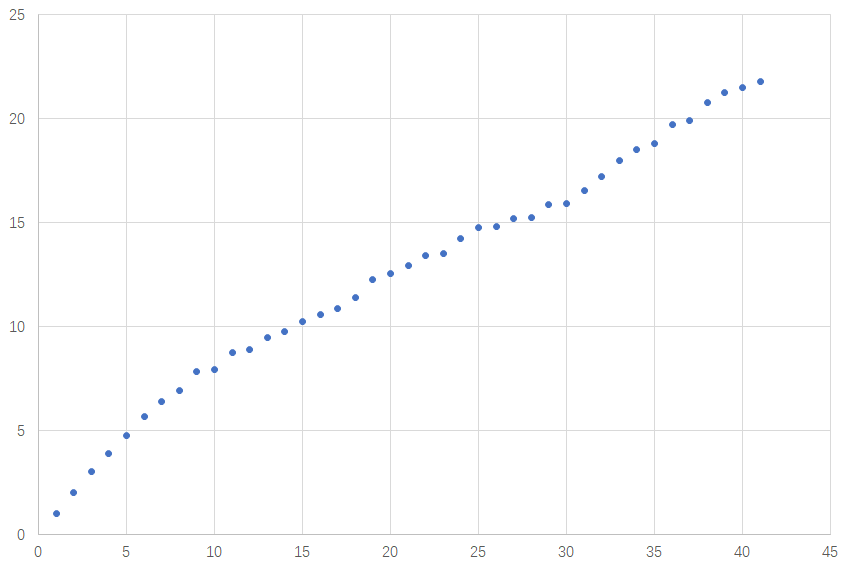
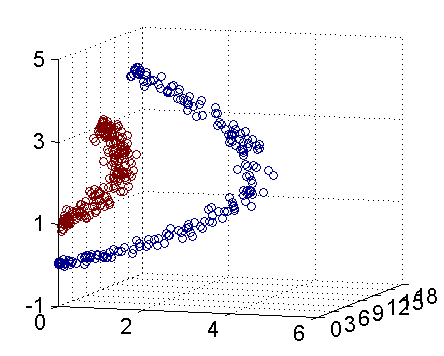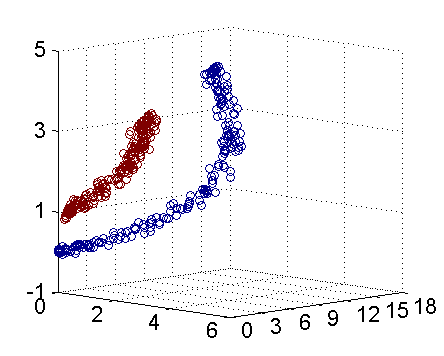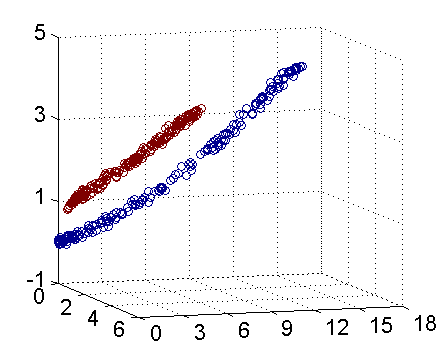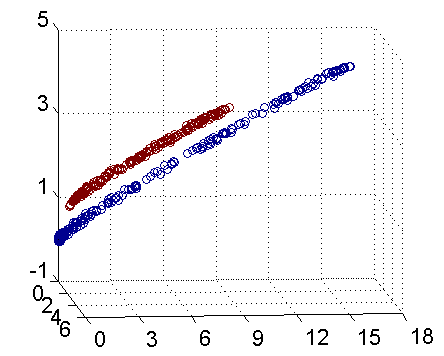
再比如下图所示的离散数据点，能否根据历史数据得到一个能表征内部关系的函数，这样当有新的x时，便可以知道y。

二、神经网络

人工神经网络（Artificial Neural Networks，简写为ANNs）也简称为神经网络（NNs）或称作连接模型（Connection Model），它是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。本质上讲就是通过线性加权和非线性函数转换来逼近真实值。详情可以访问链接 https://blog.csdn.net/illikang/article/details/82019945。

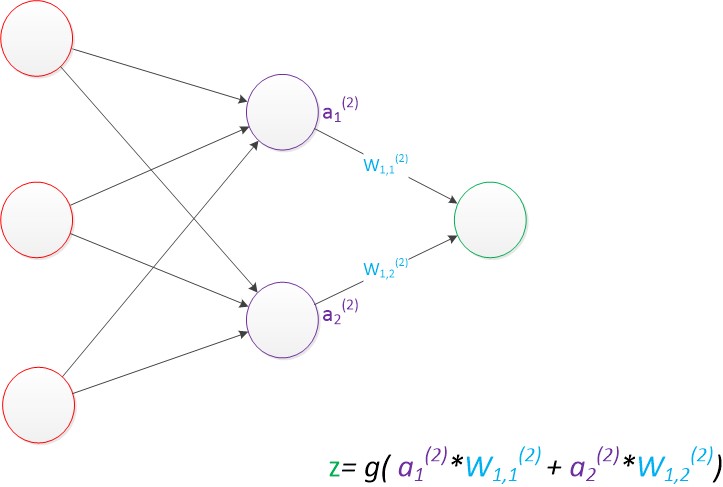
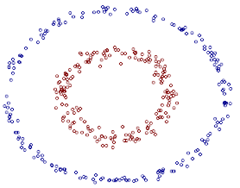
低维无法线性可分，通过映射到高维可以线性可分。（第二张三维图可以使用一个线性平面进行二分）。

梯度下降法简介

1.梯度方向是函数值变化最快的方向，沿着梯度的负方向可以最快收敛到极值点，即梯度下降法。梯度下降法是神经网络发展的基础。

2.BP算法 （链式法则）https://blog.csdn.net/qq_42570457/article/details/81454008

3.优化算法（批量梯度下降法、随机梯度下降法、自适应梯度下降法、动量梯度下降法等等）

例1：拟合线性函数
$$y=w_1{x}_1+w_2{x}_2$$
步骤：

1. 生成数据样本（添加一定的噪声）------->（X，Y)
2. 随机初始化w1,w2
3. 计算y值
4. 计算损失函数
5. 根据损失函数分别对w1和w2求偏导
6. 对w1和w2进行更新
7. 重复3-6,直到优化到满意解

不同优化算法表先表现

1、批量梯度下降算法（使用所有的样本来更新）：当数据量较大时，速度比较慢，占用内存大，但能够代表整体。

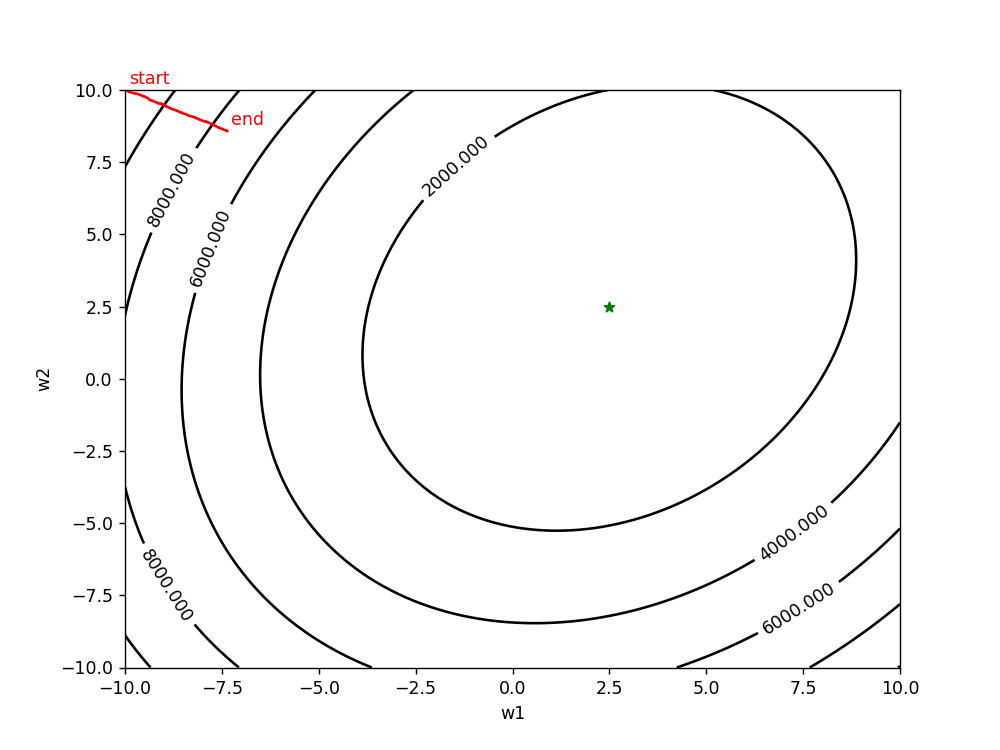
（1）lr=0.0001 epoch=500（学习率较小时，收敛的比较慢，花费的时间较长）

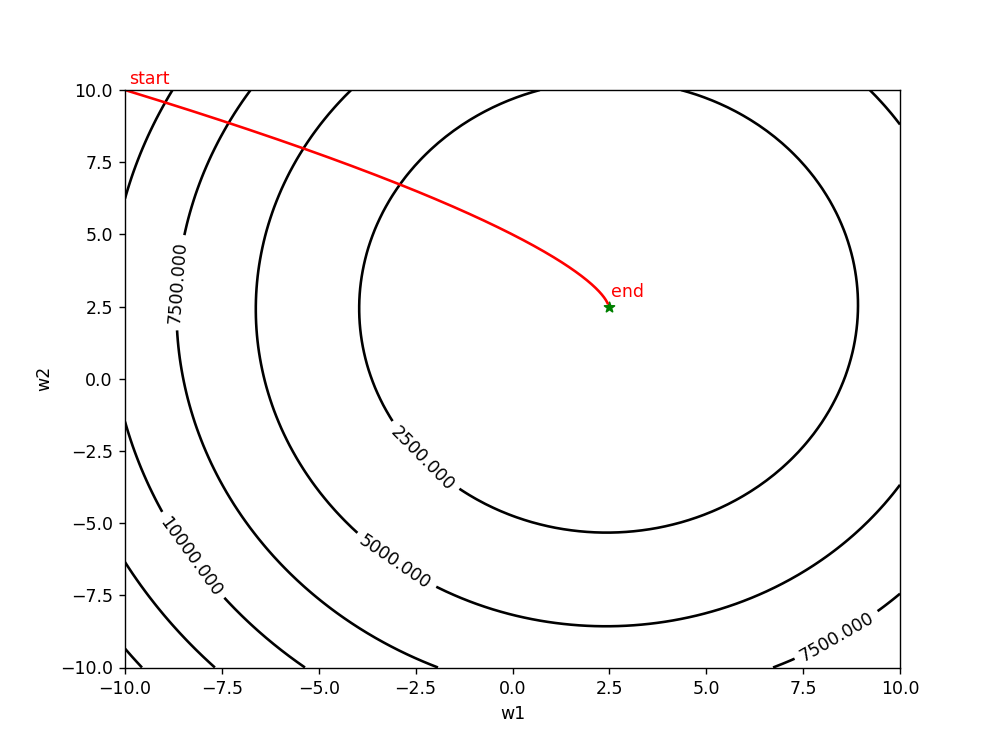
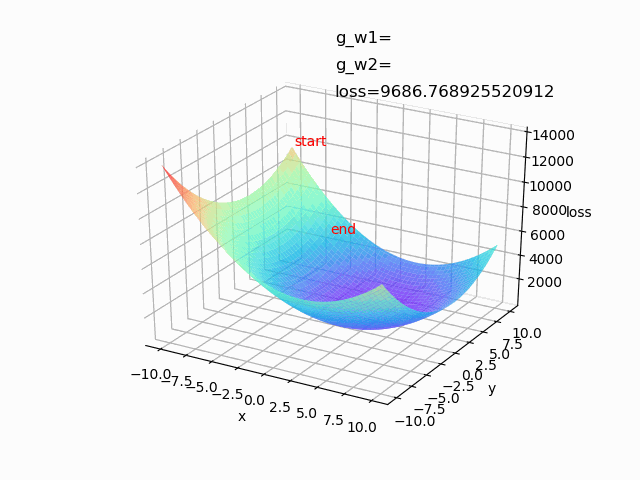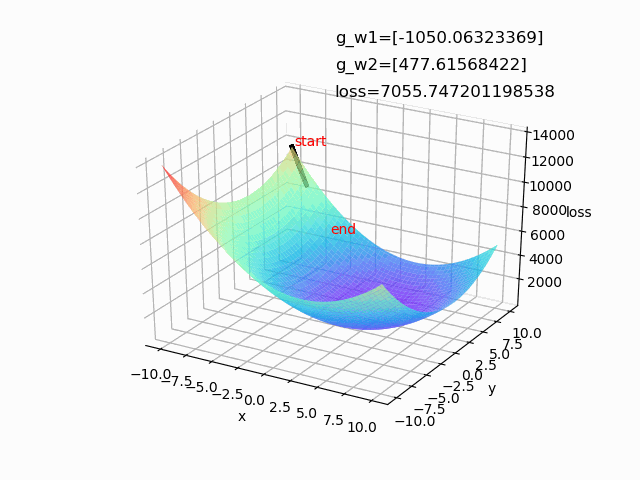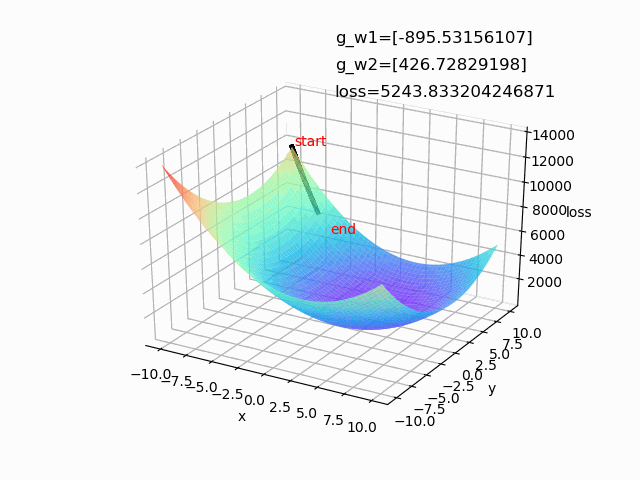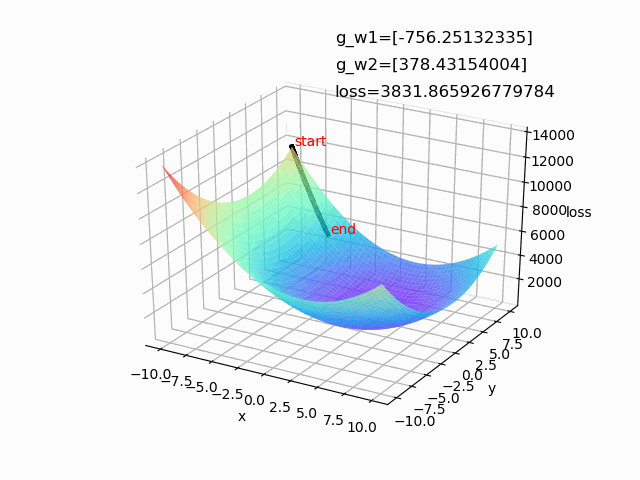
（2）lr=0.01 epoch=100（学习率较大时，前期下降较快，后期不稳定，容易摆动）

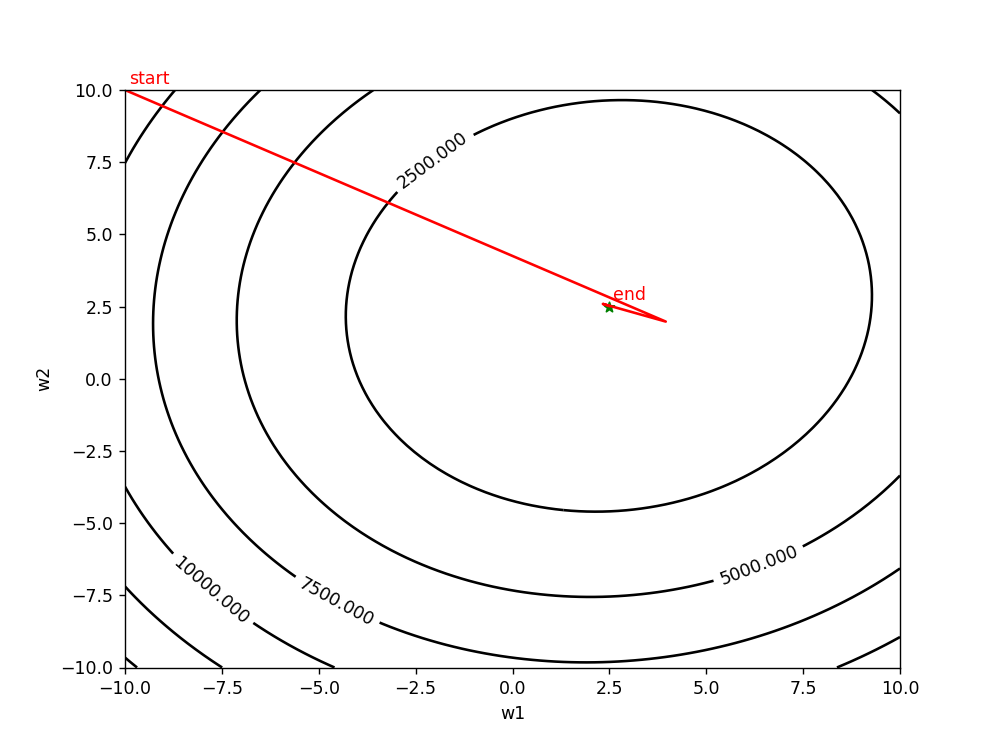
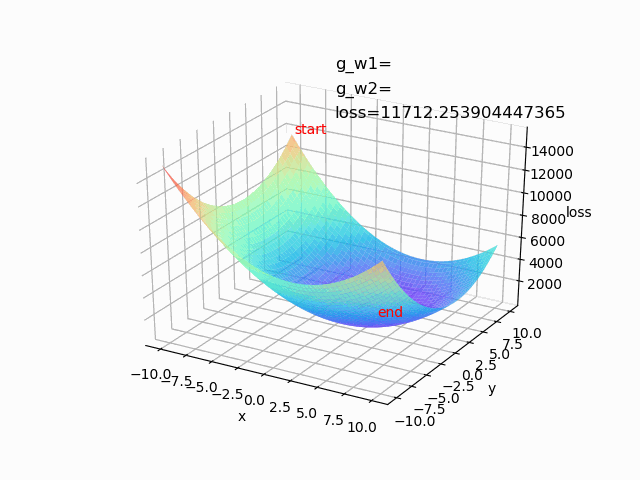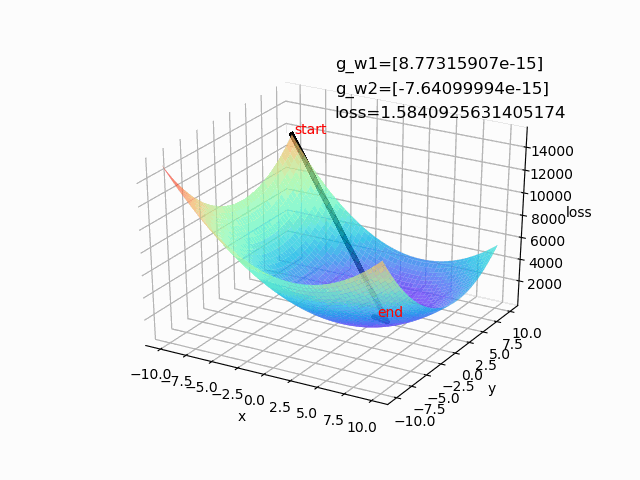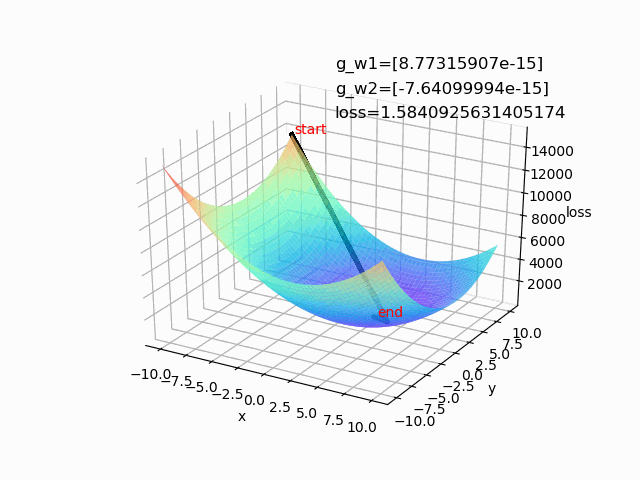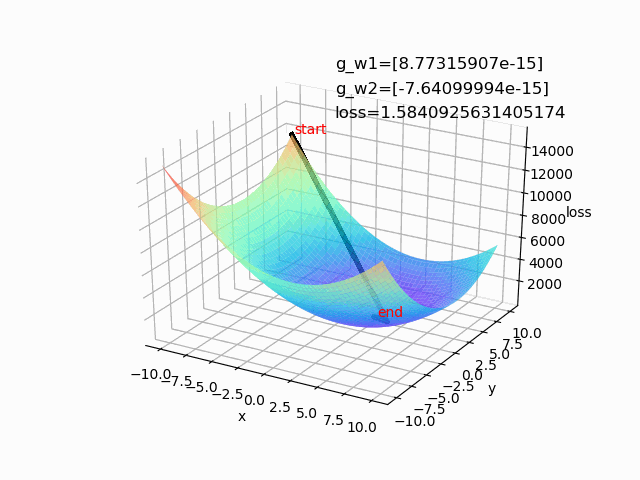
2、随机梯度下降算法（只根据一个样本来更新参数）：训练速度快，但容易陷入局部极小值，甚至很难收敛。

(1) lr=0.0001 epoch=1000

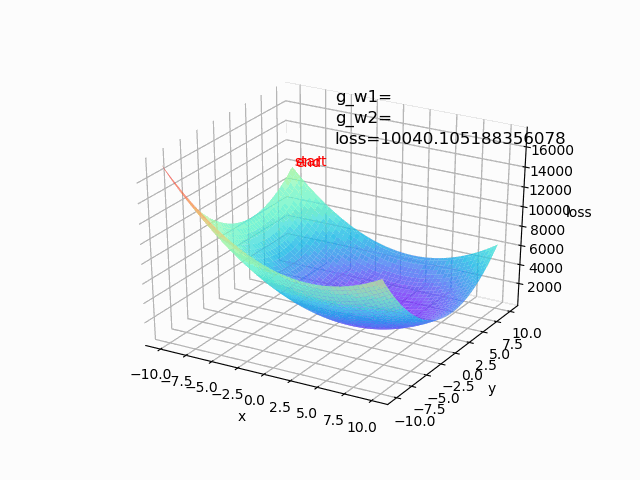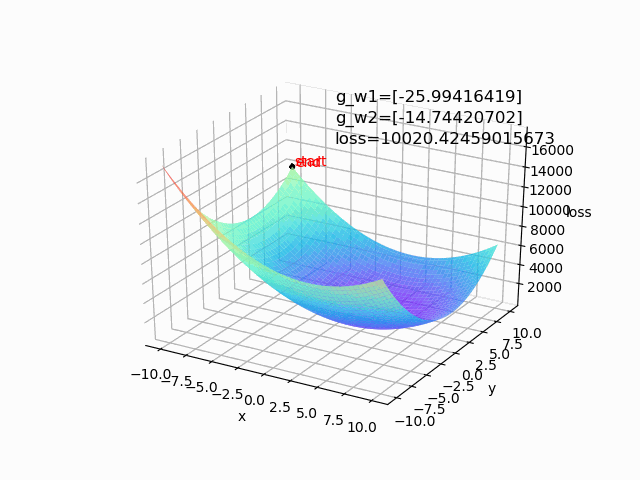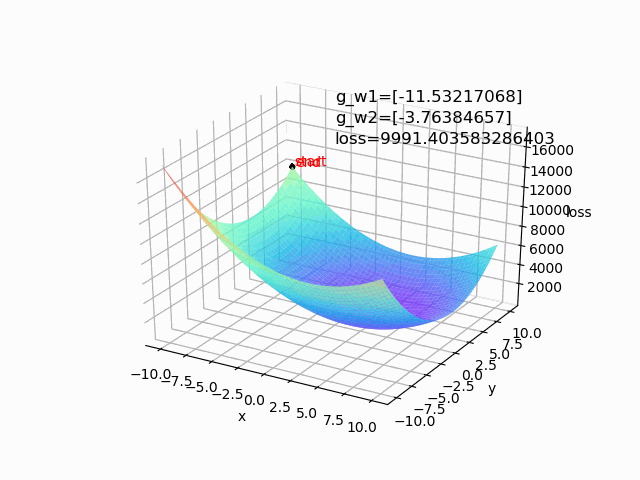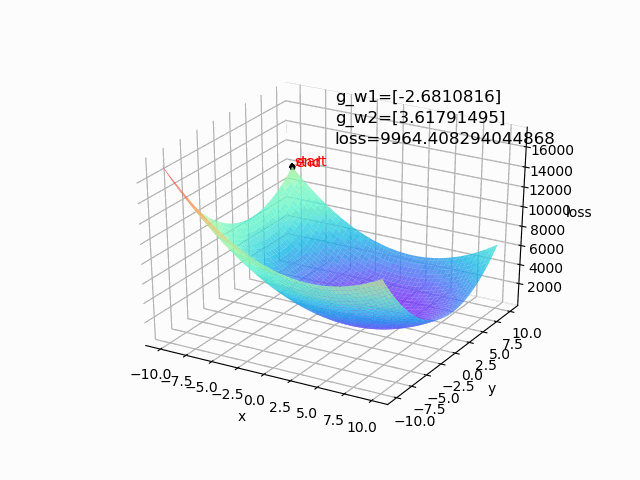
批量梯度下降算法和随机梯度下降算法是两个极端，一般会进行中和，选取小批量来更新。

3、自适应梯度下降算法（初始值学习率可以设置成较大值，随着迭代次数的增加逐渐减小，且每个参数有自己的学习率）：刚开始更新比较快，越往后会因为学习率较小而导致收敛较慢

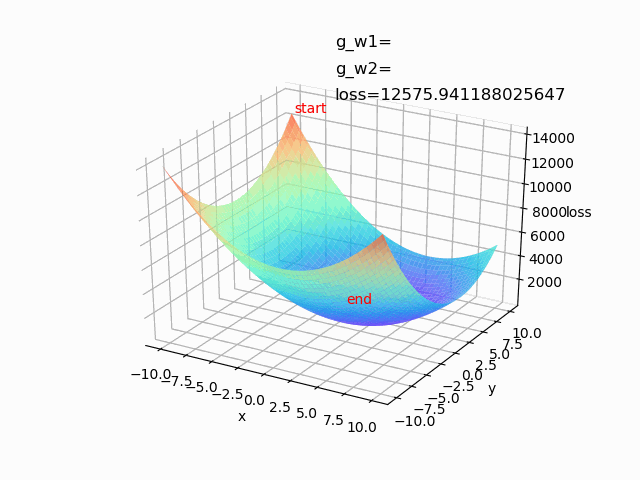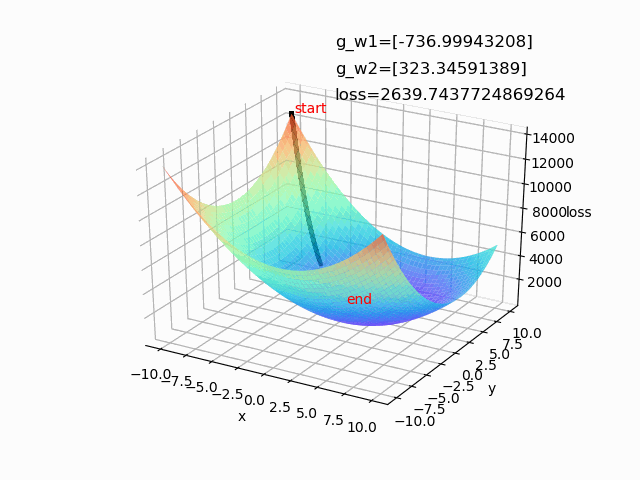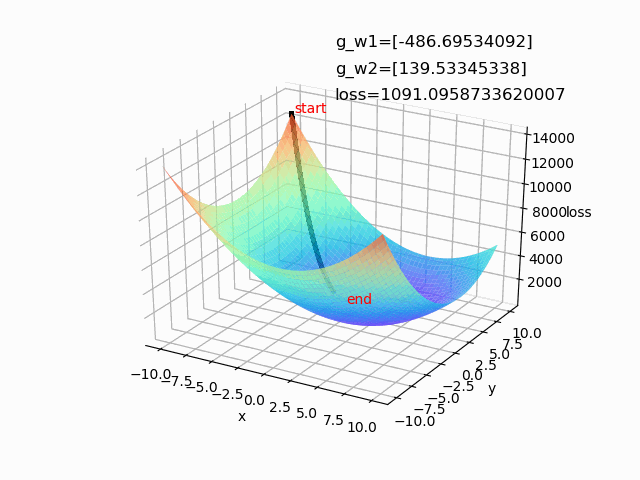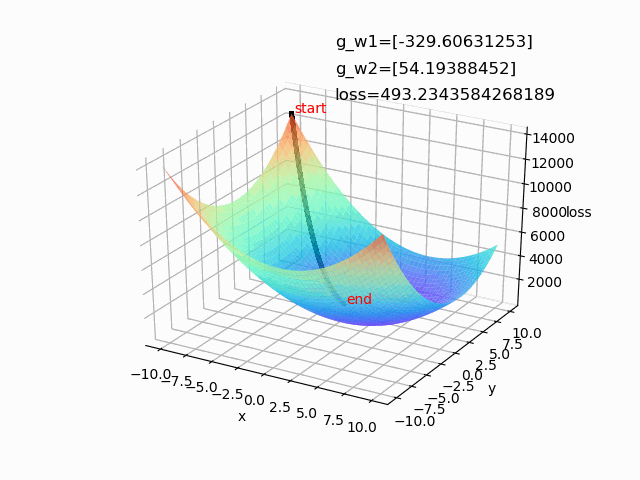
将第一种方法的学习率设置为1时，迭代过程如下图所示，可以发现效果非常差：

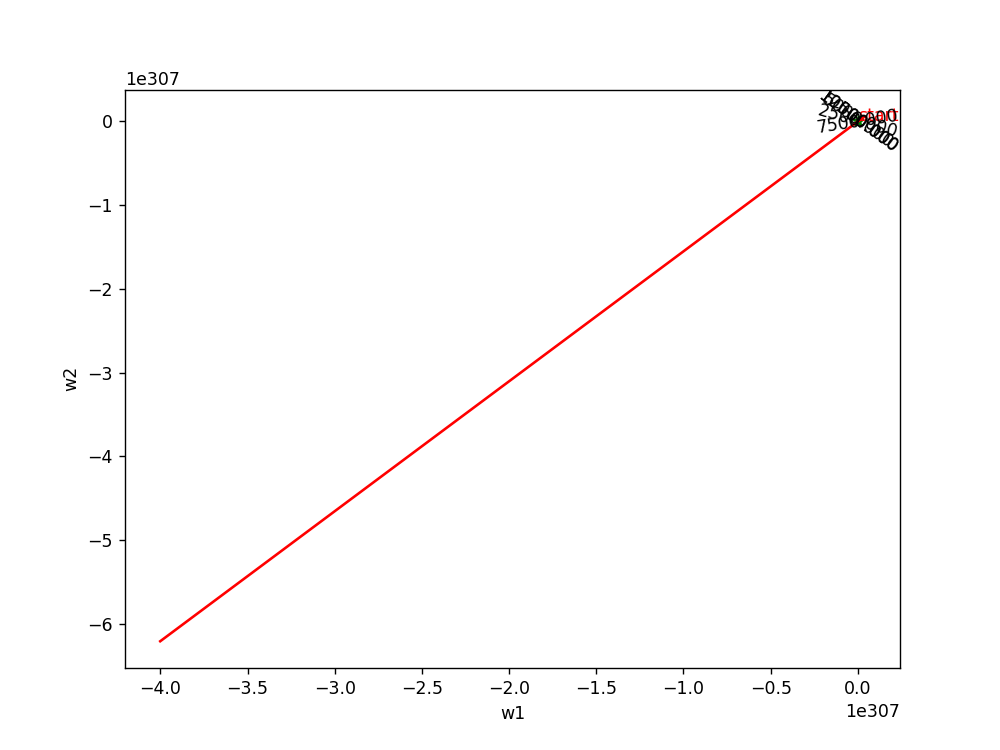
使用自适应梯度下降算法，设置lr=1,epoch=500

例2：求解损失函数极值：
$$y=x^2?y^2$$
第一个例子是一种典型的极值点为最优点，但在实际的网络中，往往存在多个局部极值点或者鞍点，因此容易陷入到鞍点。设初始值为（10，0）。

使用批量梯度下降算法，lr=0.2 epoch=500

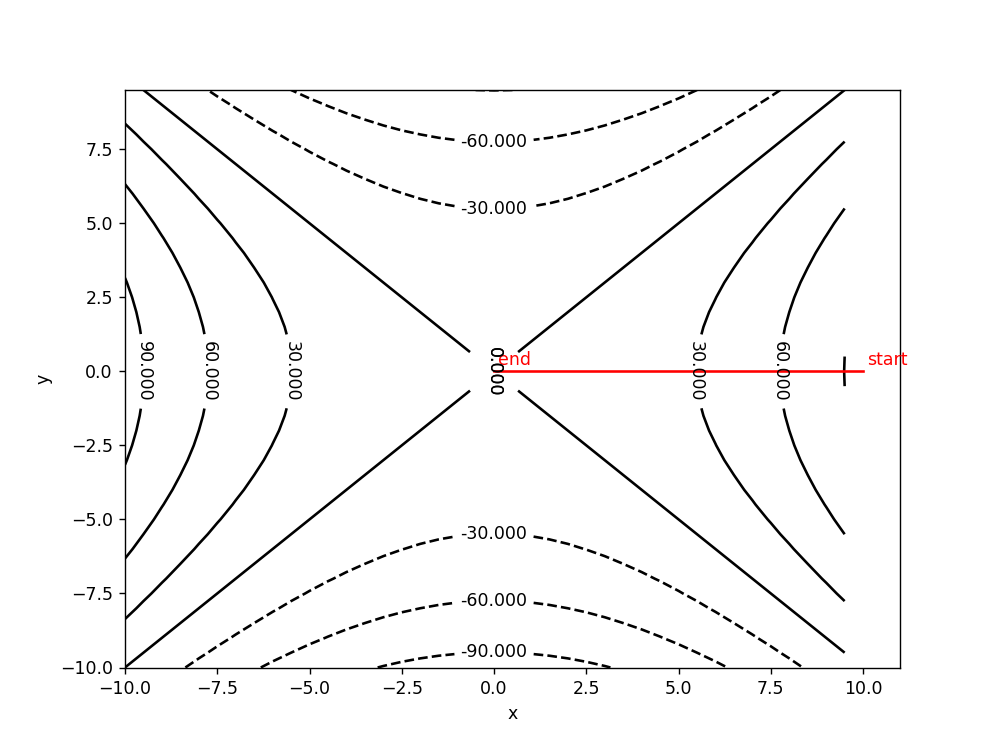
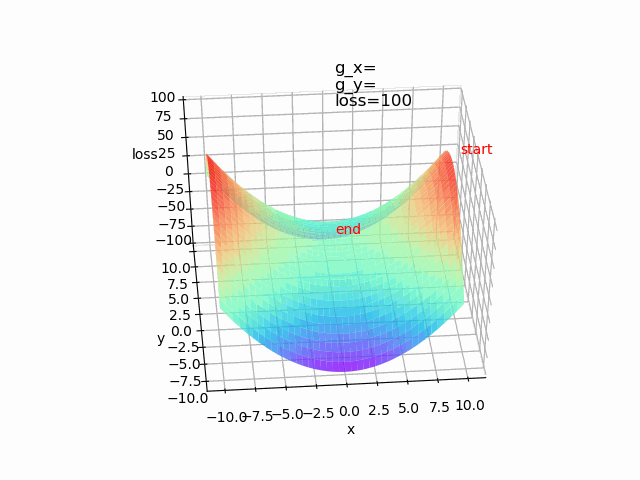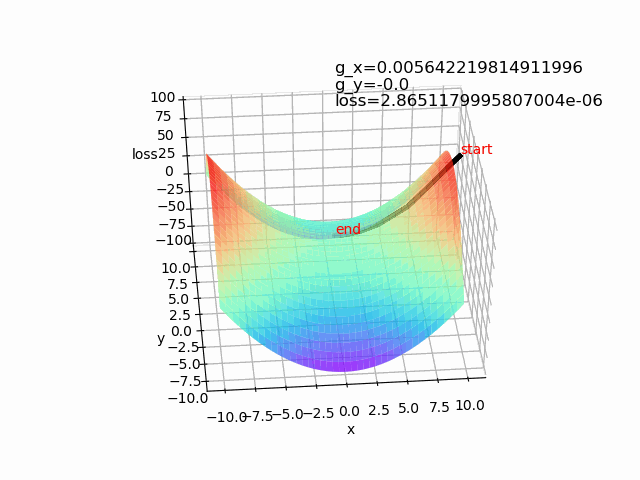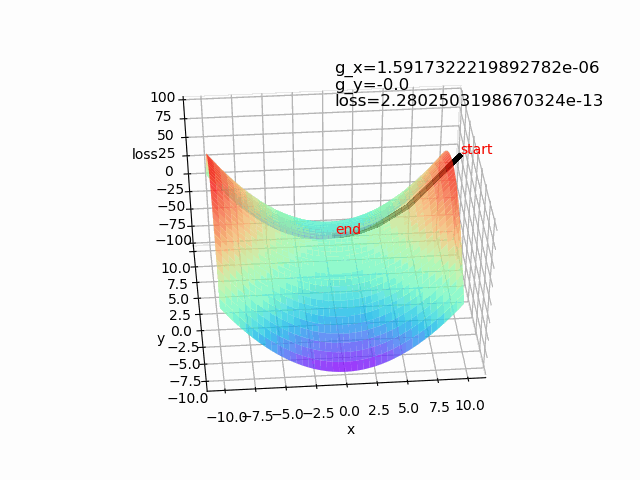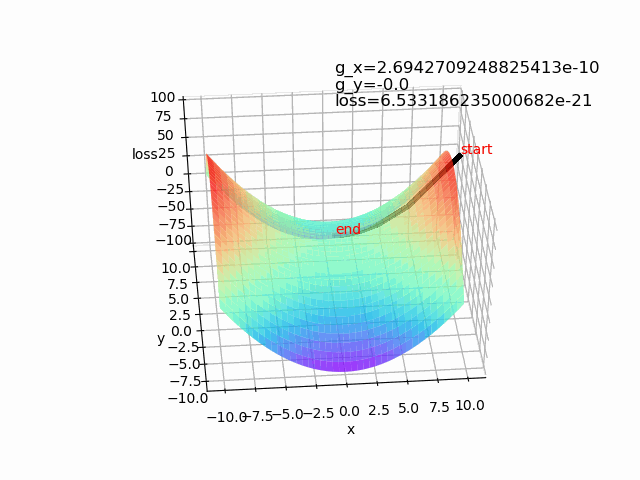
造成神经网络难以优化的一个重要（乃至主要）原因不是高维优化问题中有很多局部极值，而是存在大量鞍点。https://arxiv.org/pdf/1406.2572v1.pdf。可以使用动量梯度下降法等算法来解决。

使用批量梯度梯度下降算法，lr=1,epoch=500

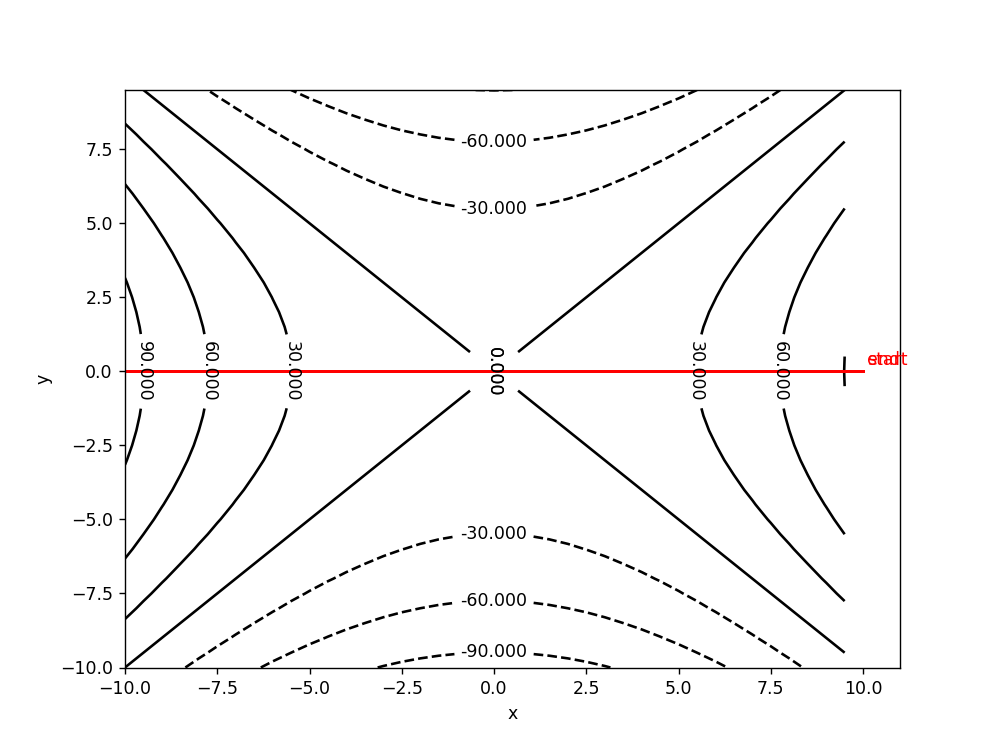
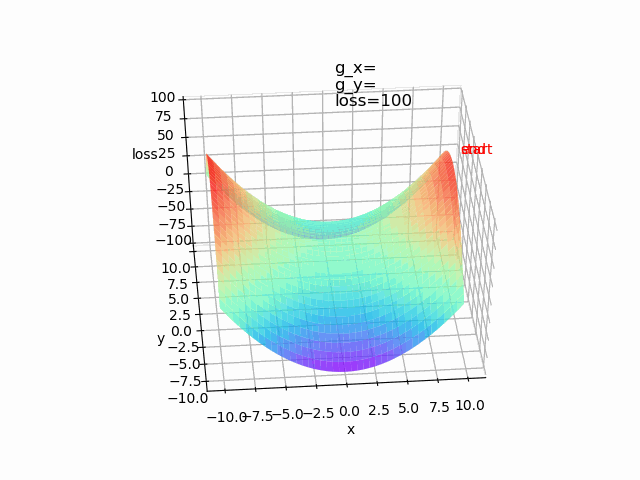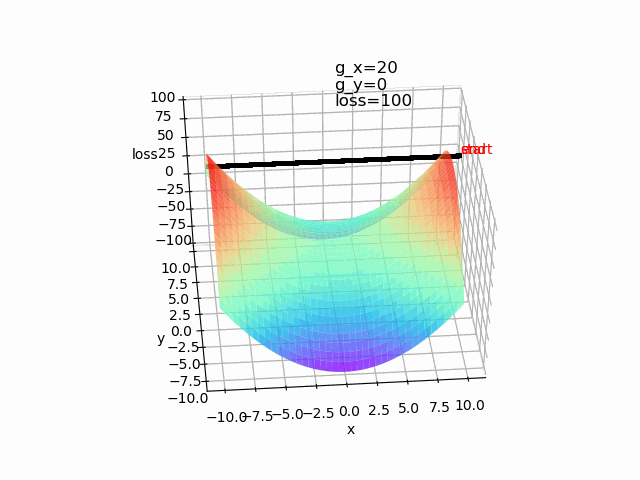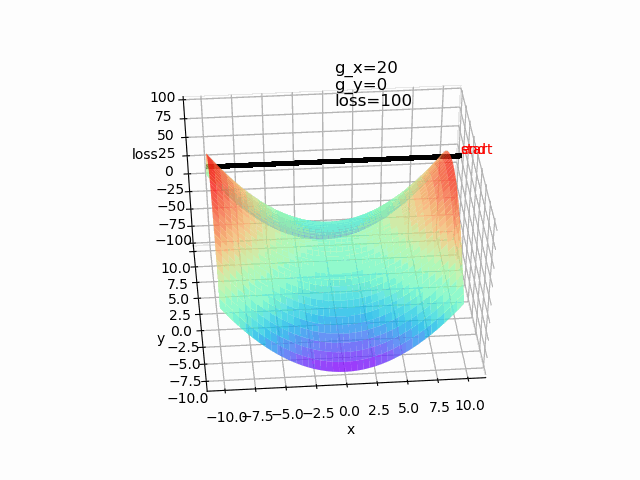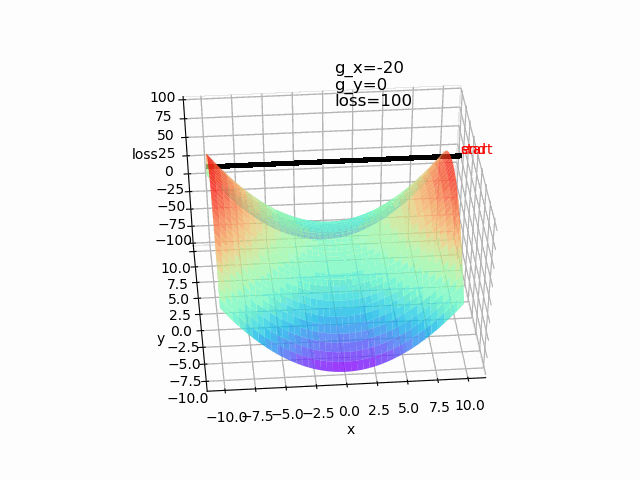
4、动量梯度下降算法（使收敛更快，减少震荡。梯度方向不变时，收敛更快，梯度方向改变时，减小震荡。收敛更稳定；有能力跳出局部极值）
设置lr=0.01，epoch=500

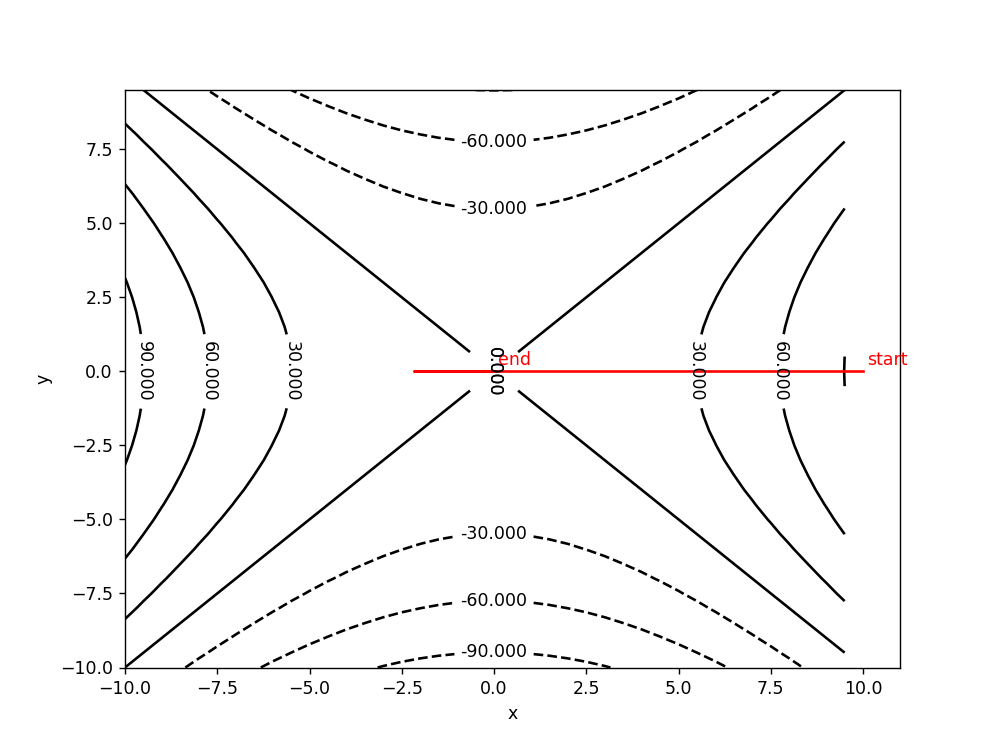
***以上无法跳出鞍点的原因是：初始值y=0，而dy=-2y，使得不管在什么时候，dy=0,因此y永远为0，从而使得迭代的轨迹在y=0这条线上徘徊。***如果重新初始化x,y的值为（10，0.01）,则：

lr=0.004,epoch=500:

添加随机扰动，设初始点为（10，0），lr=0.004,epoch=500:

除了以上将的优化算法外，还有很多梯度下降算法，目前常用的是Adam等。

说明:由于个别图片太大,自己可以根据代码进行获取,并且有些只是跑了50步,大家可以自己增加迭代次数哈.

最后附上源码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import animation
from mpl_toolkits.mplot3d import Axes3D
%matplotlib notebook

(1)拟合$$y=w_1{x}_1+w_2{x}_2$$

class Net:
    def __init__(self,n,best_w,input_size,lr):
        self.n=n
        self.input_size=input_size
        self.best_w=np.array(best_w).reshape(-1,1)
        self.w=np.array([-10.,10.]).reshape(-1,1)
        self.w1_history=[self.w[0].copy()[0]]
        self.w2_history=[self.w[1].copy()[0]]
        self.z_history=[]
        self.g_w1=[""]
        self.g_w2=[""]
        self.lr=lr
        self.w_sum=np.zeros((self.w.shape[0],self.w.shape[1]))
        self.old_gw=np.zeros((self.w.shape[0],self.w.shape[1]))
        self.get_data()
    def get_data(self):
        self.x_data=np.random.randn(self.n,self.input_size)
        noise=np.random.randn(self.n,1)
        self.y_data=self.x_data.dot(self.best_w)+0.2*noise
    def get_loss(self):
        return 0.5*np.square(self.out-self.y_data).sum()
    def forward(self):
        self.out=self.x_data.dot(self.w)
    def backward(self):
        g_l=self.out-self.y_data
        g_w=self.x_data.T.dot(g_l)
        self.w-=self.lr*g_w
        self.w1_history.append(self.w[0].copy()[0])
        self.w2_history.append(self.w[1].copy()[0])
        self.g_w1.append(g_w[0].copy())
        self.g_w2.append(g_w[1].copy())
    def Adagrad_backward(self):
        eps = 1e-6
        g_l=self.out-self.y_data
        g_w=self.x_data.T.dot(g_l)
        self.w_sum+=g_w**2
        self.w-=self.lr/np.sqrt(self.w_sum+eps)*g_w
        self.w1_history.append(self.w[0].copy()[0])
        self.w2_history.append(self.w[1].copy()[0])
        self.g_w1.append(g_w[0].copy())
        self.g_w2.append(g_w[1].copy())
    def Momentum_backward(self,gamma=0.01):
        g_l=self.out-self.y_data
        g_w=self.x_data.T.dot(g_l)
        G_w=gamma*self.old_gw+(1-gamma)*g_w
        self.old_gw=g_w
        self.w-=self.lr*G_w
        self.w1_history.append(self.w[0].copy()[0])
        self.w2_history.append(self.w[1].copy()[0])
        self.g_w1.append(G_w[0].copy())
        self.g_w2.append(G_w[1].copy())
    def SGD_backward(self):
        select_index=np.random.randint(0,self.n)
        g_l=self.out[[select_index]]-self.y_data[[select_index]]
        g_w=self.x_data[[select_index]].T.dot(g_l)
        self.w-=self.lr*g_w
        self.w1_history.append(self.w[0].copy()[0])
        self.w2_history.append(self.w[1].copy()[0])
        self.g_w1.append(g_w[0].copy())
        self.g_w2.append(g_w[1].copy())
    def surface_view(self):
        fig = plt.figure() 
        ax3 = fig.gca(projection='3d')
        w1=np.linspace(-10,10,100)
        w2=np.linspace(-10,10,100)
        X,Y = np.meshgrid(w1,w2)
        y_data=np.concatenate([self.y_data for i in range(X.shape[1])],axis=1)
        Z=np.zeros((X.shape[0],X.shape[1]))
        for i in range(len(Y)):
            temp_X=np.concatenate((X[0],Y[i]),axis=0).reshape(-1,X.shape[1])
            Z[i]=0.5*np.square(self.x_data.dot(temp_X)-y_data).sum(axis=0)
        ax3.plot_surface(X,Y,Z,cmap='rainbow',alpha=0.75)
        ax3_x,ax3_y,ax3_z=[],[],[]
        ax3.plot([],[],[],color="black",linewidth=3.0)
        gx_text=ax3.text(0,0,22000,"",fontsize=12)
        gy_text=ax3.text(0,0,20000,"",fontsize=12)
        loss_text=ax3.text(0,0,18000,"",fontsize=12)
        def view_update(num):
            ax3_x.append(self.w1_history[num])
            ax3_y.append(self.w2_history[num])
            ax3_z.append(self.z_history[num])
            ax3.plot(ax3_x,ax3_y,ax3_z,color="black",linewidth=3.0)
            gx_text.set_text("g_w1={}".format(self.g_w1[num]))
            gy_text.set_text("g_w2={}".format(self.g_w2[num]))
            loss_text.set_text("loss={}".format(self.z_history[num]))
            return (ax3,gx_text,gy_text,loss_text)
        ani = animation.FuncAnimation(fig=fig,func=view_update,frames=np.arange(0,len(self.w1_history)),interval=80,blit=True)
        ax3.text(self.w1_history[0]+0.1, self.w2_history[0]+0.2, self.z_history[0]+0.2,'start', color='r')
        ax3.text(self.w1_history[-1]+0.1, self.w2_history[-1]+0.2, self.z_history[-1]+0.2,'end', color='r')
        ax3.set_xlabel("x")
        ax3.set_ylabel("y")
        ax3.set_zlabel("loss")
        ani.save('二元一次函数agd小0.0001.gif', writer='imagemagick', fps=10)
        plt.show()
        
    def view(self):
        w1=np.linspace(-10,10,100)
        w2=np.linspace(-10,10,100)
        X,Y = np.meshgrid(w1,w2)
        y_data=np.concatenate([self.y_data for i in range(X.shape[1])],axis=1)
        Z=np.zeros((X.shape[0],X.shape[1]))
        for i in range(len(Y)):
            temp_X=np.concatenate((X[0],Y[i]),axis=0).reshape(-1,X.shape[1])
            Z[i]=0.5*np.square(self.x_data.dot(temp_X)-y_data).sum(axis=0)
        plt.figure(figsize=(8,6))
        contour=plt.contour(X,Y,Z,6,colors='k',offset=-1)
        plt.clabel(contour,fontsize=10,colors='k')
        plt.plot(self.w1_history,self.w2_history,color="r")
        plt.text(self.w1_history[0]+0.1, self.w2_history[0]+0.2,'start', color='r')
        plt.text(self.w1_history[-1]+0.1, self.w2_history[-1]+0.2,'end', color='r')
        plt.scatter(self.best_w[0],self.best_w[1],marker="*",color="green")
        plt.xlabel('w1')
        plt.ylabel('w2')
        plt.show()
    def train(self):
        self.forward()
        loss=self.get_loss()
        self.z_history.append(loss)
        epoch=50
        for i in range(epoch):
            self.Adagrad_backward()
            self.forward()
            loss=self.get_loss()
            self.z_history.append(loss)
        self.view()
        self.surface_view()

(2)求解$$y=2x^2+1$$

class Net:
    def __init__(self,init_x,init_y,lr):
        self.x=init_x
        self.y=init_y
        self.lr=lr
        self.x_history=[init_x]
        self.y_history=[init_y]
        self.z_history=[init_x**2-init_y**2]
        self.g_x=[""]
        self.g_y=[""]
        self.x_sum=0
        self.y_sum=0
        self.old_gx=0
        self.old_gy=0
    def surface_view(self):
        fig = plt.figure() 
        ax3 = fig.gca(projection='3d')
        x_data=np.arange(-10,10,0.5)
        y_data=np.arange(-10,10,0.5)
        X, Y = np.meshgrid(x_data, y_data)
        Z = X**2-Y**2
        ax3.plot_surface(X,Y,Z,cmap='rainbow',alpha=0.75)
        ax3_x,ax3_y,ax3_z=[],[],[]
        ax3.plot([],[],[],color="black",linewidth=3.0)
        gx_text=ax3.text(0,0,210,"",fontsize=12)
        gy_text=ax3.text(0,0,190,"",fontsize=12)
        loss_text=ax3.text(0,0,170,"",fontsize=12)
        def view_update(num):
            ax3_x.append(self.x_history[num])
            ax3_y.append(self.y_history[num])
            ax3_z.append(self.z_history[num])
            ax3.plot(ax3_x,ax3_y,ax3_z,color="black",linewidth=3.0)
            gx_text.set_text("g_x={}".format(self.g_x[num]))
            gy_text.set_text("g_y={}".format(self.g_y[num]))
            loss_text.set_text("loss={}".format(self.z_history[num]))
            return (ax3,gx_text,gy_text,loss_text)
        ani = animation.FuncAnimation(fig=fig,func=view_update,frames=np.arange(0,len(self.x_history)),interval=200,blit=True)
        ax3.text(self.x_history[0]+0.1, self.y_history[0]+0.2, self.z_history[0]+0.2,'start', color='r')
        ax3.text(self.x_history[-1]+0.1, self.y_history[-1]+0.2, self.z_history[-1]+0.2,'end', color='r')
        ax3.set_xlabel("x")
        ax3.set_ylabel("y")
        ax3.set_zlabel("loss")
        ax3.view_init(elev=44,azim=-95)#改变绘制图像的视角,即相机的位置,azim沿着z轴旋转，elev沿着y轴
        ani.save('梯度下降算法小2.gif', writer='imagemagick', fps=10)
        plt.show()
    def view(self):
        plt.figure(figsize=(8,6))
        x_data=np.arange(-10,10,0.5)
        y_data=np.arange(-10,10,0.5)
        X, Y = np.meshgrid(x_data, y_data)
        Z = X**2-Y**2
        contour=plt.contour(X,Y,Z,6,colors='k',offset=-1)
        plt.clabel(contour,fontsize=10,colors='k')
        plt.plot(self.x_history,self.y_history,color="r")
        plt.text(self.x_history[0]+0.1, self.y_history[0]+0.2,'start', color='r')
        plt.text(self.x_history[-1]+0.1, self.y_history[-1]+0.2,'end', color='r')
        plt.xlabel('x')
        plt.ylabel('y')
        plt.show()
    def get_loss(self):
        return self.x**2-self.y**2
    def backward(self):
        g_x=2*self.x
        g_y=-2*self.y
        self.x-=self.lr*g_x
        self.y-=self.lr*g_y
        self.x_history.append(self.x)
        self.y_history.append(self.y)
        self.g_x.append(g_x)
        self.g_y.append(g_y)
    def jump_min(self):
        g_x=2*self.x
        g_y=-2*self.y
        self.x-=self.lr*g_x
        self.y-=self.lr*g_y
        self.x_history.append(self.x)
        self.y_history.append(self.y)
        self.g_x.append(g_x)
        self.g_y.append(g_y)
    def Adagrad_backward(self):
        eps = 1e-6
        g_x=2*self.x
        g_y=-2*self.y
        self.x_sum+=g_x**2
        self.y_sum+=g_y**2
        self.x-=self.lr/np.sqrt(self.x_sum+eps)*g_x
        self.y-=self.lr/np.sqrt(self.y_sum+eps)*g_y
        self.x_history.append(self.x)
        self.y_history.append(self.y)
        self.g_x.append(g_x)
        self.g_y.append(g_y)
    def RMSProp_backward(self,gamma=0.2):
        eps = 1e-6
        g_x=2*self.x
        g_y=-2*self.y
        self.x_sum=gamma*self.x_sum+(1-gamma)*g_x**2
        self.y_sum=gamma*self.y_sum+(1-gamma)*g_y**2
        self.x-=self.lr/np.sqrt(self.x_sum+eps)*g_x
        self.y-=self.lr/np.sqrt(self.y_sum+eps)*g_y
        self.x_history.append(self.x)
        self.y_history.append(self.y)
        self.g_x.append(g_x)
        self.g_y.append(g_y)
    def Momentum_backward(self,gamma=0.9):
        g_x=2*self.x
        g_y=-2*self.y+0.01*np.random.rand()
        G_x=gamma*self.old_gx+g_x
        G_y=gamma*self.old_gy+g_y
        self.old_gx=g_x
        self.old_gy=g_y
        self.x-=self.lr*G_x
        self.y-=self.lr*G_y
        self.x_history.append(self.x)
        self.y_history.append(self.y)
        self.g_x.append(G_x)
        self.g_y.append(G_y)
    def train(self):
        for i in range(50): 
            self.Momentum_backward()
            self.z_history.append(self.get_loss())
        self.surface_view()
        self.view()

觉得小墨的文章对您有帮助的话,记得点赞加关注哦!