- 此文章是基于pytorch官方教程的中文版https://pytorch123.com/SecondSection/autograd_automatic_differentiation/写的
- 因为自己在理解的时候并不能很好的理解这个autograd里面的backward自动求梯度是怎么回事,雅各比点积又是怎么回事,所以写了这个小白版的
- 写的不全,官方写的一些注释我有的没有加上,而且官方有2个地方写的不太容易让我这种小白理解,修改了一下。
- 本文借鉴有3:第一篇博客写的很好
https://blog.csdn.net/weixin_39715652/article/details/111167464?utm_medium=distribute.pc_relevant.none-task-blog-2defaultbaidujs_title~default-4.control&spm=1001.2101.3001.4242
pytorch官方教程的中文版https://pytorch123.com/SecondSection/autograd_automatic_differentiation/
https://zhuanlan.zhihu.com/p/76630905
- 本文将直接从backward部分开始
如果你想计算导数,你可以调用 Tensor.backward()。如果 Tensor 是标量(即它包含一个元素数据),则不需要指定任何参数backward(),但是如果它有更多元素,则需要指定一个gradient 参数来指定张量的形状。
上面这段是官方对backward的解释,说这么一堆无非是表述,你想求gradient梯度,请用backward这个函数(为什么是这个名字,跟神经网络的原理有关,神经网络求梯度是从后往前求的,可以自己找资料看看)。
下面我把backward这里用到的例子拿出来,官方文档这里写的不连贯,它用了x y z out这几个变量去解释backward,但是中间又插了例子去解释了这个:
requires_grad_( … ) 会改变张量的 requires_grad 标记
x = torch.ones(2, 2, requires_grad=True)
y = x + 2
z = y * y * 3
out = z.mean()
# 求梯度啦
out.backward()
# 打印x的梯度
print(x.grad)
从这里能看出x是一个全1的2*2的张量,z是个简单的函数:z = 3(x+2)^2,z不是一个标量,但是out表示平均数,它是一个标量。
另外必须注意的一点是,x由于是我们定义的变量,它作为叶子结点,当我们调用out的backward方法后会根据链式法则自动计算出叶子节点x的梯度值。所以自己可以手算下,out对x的导数是4.5:
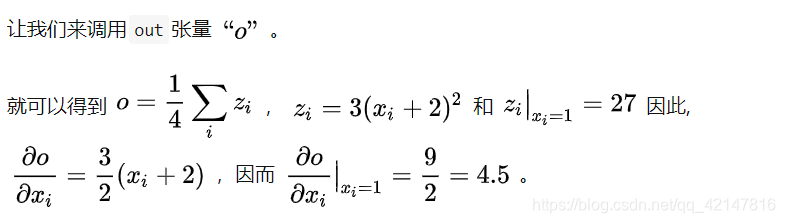
相对的,对于非标量,或者说向量,如果你有了解雅克比行列式,(不了解的可以百度下,很简单),你就会知道,对向量函数求导,可以写成雅克比行列式。
同时,官方文档在这里的例子不太好,不太利于手撸结果验证,所以我们改一下:
# 官方写法:随机数向量
# x = torch.randn(3, requires_grad=True)
# 我们换成全1向量
x = torch.ones(3, requires_grad=True)
# y不变
y = x * 2
# 这个操作我们也不要了,data.norm作用是对张量y每个元素进行平方,然后对它们求和,最后取平方根。
# 这些操作计算就是所谓的L2或欧几里德范数 。
# while y.data.norm() < 1000:
# y = y * 2
print(y)
输出y长这样:
tensor([2., 2., 2.], grad_fn=)
然后利用backward求梯度,但是需要多一个v向量作为这个方法的参数,指定x的每一维的赋值*(不知道这样说准确与否)*
# [0.1, 1.0, 0.0001] 分别是赋的x的值
v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
y.backward(v)
print(x.grad)
十分容易验证,输出应该是这样一个张量:
tensor([2.0000e-01, 2.0000e+00, 2.0000e-04])
写在后面:
- 这个是想记录一下又一次卡在匪夷所思的地方,想跳过吧,又觉得自己在划水,跳过的地方以后还会成为拦路虎,不跳过吧,翻来覆去找资料看,没什么头绪
- 头绪的解决,其实是看了3blue1brown的一个视频,他回答:当看数学书看了7遍8遍还没有头绪时应该怎么办,是不是我真的没有天分。作者回答说,或许是这个资料写的不对你口味,或许是它写的不好,更或许是作者默认你已经掌握了一些前提知识,所以没有提到,有些人学数学是靠天分,但是nature or nurture是一个没有答案的问题,更多人是后天培养
- 然后我就抱着不抛弃不放弃的精神,认为“pytorch”官方教程不够符合我的口味,自己更改了上面两点内容,摸索出来了自己的理解。QAQ。果然还是太菜了QAQ