[人工智能]集成聚类之Enhanced Ensemble Clustering via Fast Propagation of Cluster-Wise Similarities论文大纲整理及其翻译

前述

• 本文是2021年发表在 IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS:SYSTEMS上的一篇文章。
• 论文链接请戳这里

论文贡献

• 一种新的similarity衡量方式，通过从每个聚类结点开始随机游走，从而捕捉更高级别的ensemble information。
• 提出了一种ECA矩阵，这种矩阵同时反应了对象的共生关系和聚类的结构信息。
• 提出了两种一致性函数（共识函数）用于对得到的ECA矩阵进行聚类。

Notation

• $X=(x_1,x_2,...x_N)$ :样本数据集。
• Π = { π 1 , . . . π M } Π=\{\pi^1,...\pi^M\} Π={π1,...πM}:表示M个基聚类器，${\pi }^{?}$表示集成聚类的结果。
• π m = { C 1 m , C 2 m , . . . , C n m m } , C j m \pi^m=\{C^m_1,C^m_2,...,C^m_{n^m}\},C^m_j πm={C1m?,C2m?,...,Cnmm?},Cjm?代表第m个基聚类器中的第j个簇。
• $n^m$代表第m个基聚类器中的簇个数，$N_c={\sum }_{m=1}^M{n}^m$代表所有簇的个数。

Propagation of cluster-wise similarities

这部分用于阐明如何进行随机游走，以及产生一个新的cluster-wise similarity matrix（该矩阵并不是ECA矩阵）。具体而言，分为以下两个步骤。

• 1）构造图G（V,E），其中V代表所有的簇的集合，边集 E = { e i j = J a c c a r d ( C i , C j ) ∣ 0 ? i , j ? N c } E=\{e_{ij}=Jaccard(C_i,C_j)|0\leqslant i,j\leqslant N^c\} E={eij?=Jaccard(Ci?,Cj?)∣0?i,j?Nc}这是initial similarity graph。关于Jaccard相关系数可以点击这里。
• 2）加入multiscale信息，具体的方法为首先构造一个概率转移矩阵，再通过概率转移矩阵构造一个新的相似度矩阵。
  ??????2.1)构建单步概率转移矩阵
  ????????????????????????????
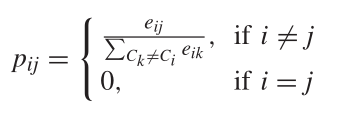
  ??????2.2)多步概率转移矩阵
  ??????????????????????????
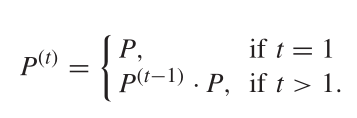
• 从节点$C_i$开始进行t步的随机游走（random walk），定义符号 P i : ( 1 : t ) = { P i : ( 1 ) , P i : ( 2 ) , . . . , P i : ( t ) } P^{(1:t)}_{i:}=\{P^{(1)}_{i:},P^{(2)}_{i:},...,P^{(t)}_{i:}\} Pi:(1:t)?={Pi:(1)?,Pi:(2)?,...,Pi:(t)?}代表随机游走的轨迹，其中 P i : ( t ) = { P i 1 ( t ) , P i 2 ( t ) , . . . , P i N ( t ) } P^{(t)}_{i:}=\{P^{(t)}_{i1},P^{(t)}_{i2},...,P^{(t)}_{iN}\} Pi:(t)?={Pi1(t)?,Pi2(t)?,...,PiN(t)?}
• 新的相似度矩阵 Z = { z i j } N c ? N c Z=\{z_{ij}\}_{N_c*N_c} Z={zij?}Nc??Nc??，其中$z_{ij}=Sim(P_{i:}^{(1:t)},P_{j:}^{(1:t)})$,$Sim(?,?)$是某种相似度衡量方式。文章采用的是余弦相似度。

ECA（Enhanced co-association matrix）矩阵构建

• 得到相似度矩阵Z以后，继续将其（簇级别）映射至对象级别。
• 首先，对于每一个基聚类器，构建一个矩阵$A^m$，这个矩阵描述了每一个簇中包含有的样本。再根据$A^m$构建共关联矩阵$A$。具体如图下图所示。
  ???????????????
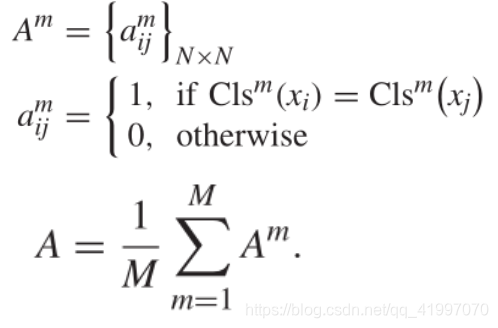
• 根据两个相似度矩阵$Z$和$A$，得到新的ECA矩阵，这个矩阵不仅考虑了co-coccurrence，还考虑了multiscale cluster-wise similarity。
  ???????????????

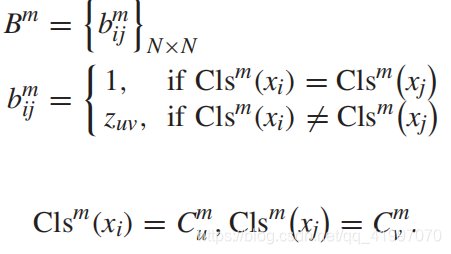
两种共识函数（consensus function）

在得到了上述的ECA矩阵以后，我们可以对其进行任意方法的聚类，文章中提供了两种方法。分别为：

• 基于层次聚类（hierarchical clustering）的共识函数——使用average-link对得到的ECA进行聚类。
• 基于元聚类（meta-clustering）的的共识函数——这个和CBGF里面用到的方法一样，但是这篇文章里把他称为ECPCS-MC。

实验

• 待补充