先给出回归的实际应用例子：
- 股票预测（stock market forecast）
- 自动驾驶（self-driving car）
- 推荐系统（recommendation）
接下来，我们将通过宝可梦进化的例子，来学习认识回归。
1.宝可梦进化的例子
-
step1：选择模型——线性模型
b：表示偏移量
xi：表示各种特征，如生命值、体重、身高…
wi：表示各种特征的权重 -
step2：找出最好的function——损失函数
首先，b和w都是未知数，所以在这个函数集合中，包含了成千上万个函数，那么我们怎么知道一个function是好是坏呢？没错，就是损失函数（loss function）
下面这个图是10组training data，this is real data
xcp：进化前的cp值
y:进化后的cp值
这就是损失函数的例子，我们可以很容易看出，这是一个最小二乘法的式子。当损失函数越小，说明模型就越好。input：a function，output：how bad it is。
- step3:gradient descent(梯度下降)
梯度下降的作用是优化参数w和b。
当只有一个参数w时：
η：我们可以称为“步长”，或者learning rate。
由图可知，当w的偏导小于0时，w的值向右移动；当w的偏导大于0时，w的值向左移动，直到不能移动为止，但是好像那不是最小值！还好，在线性模型中我们不会遇到这个问题。
当有两个的参数的情况：
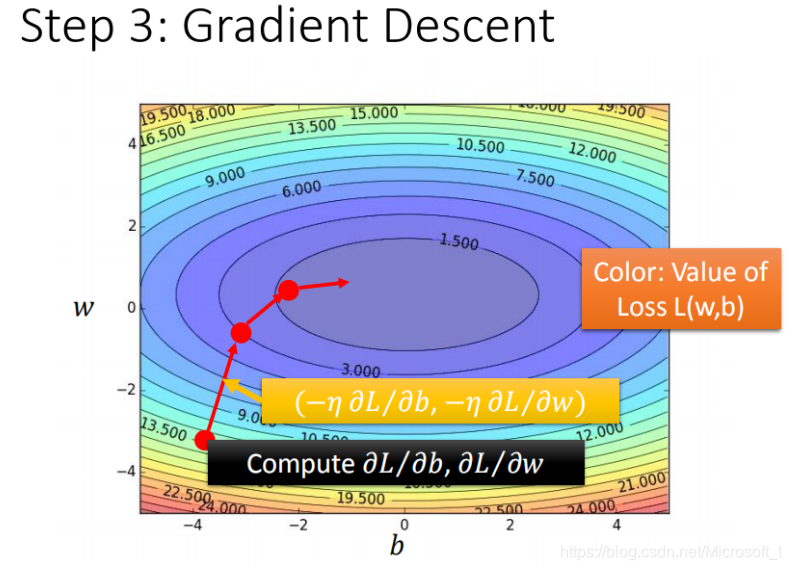
每一条线围成的圈就是等高线，代表损失函数的值，颜色约深的区域代表的损失函数越小
红色的箭头代表等高线的法线方向
2.进一步优化模型
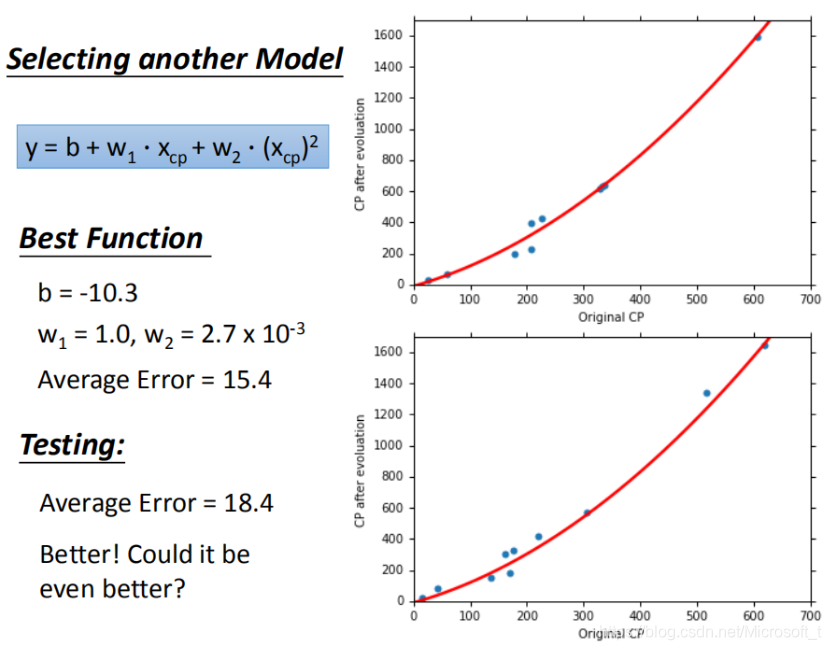
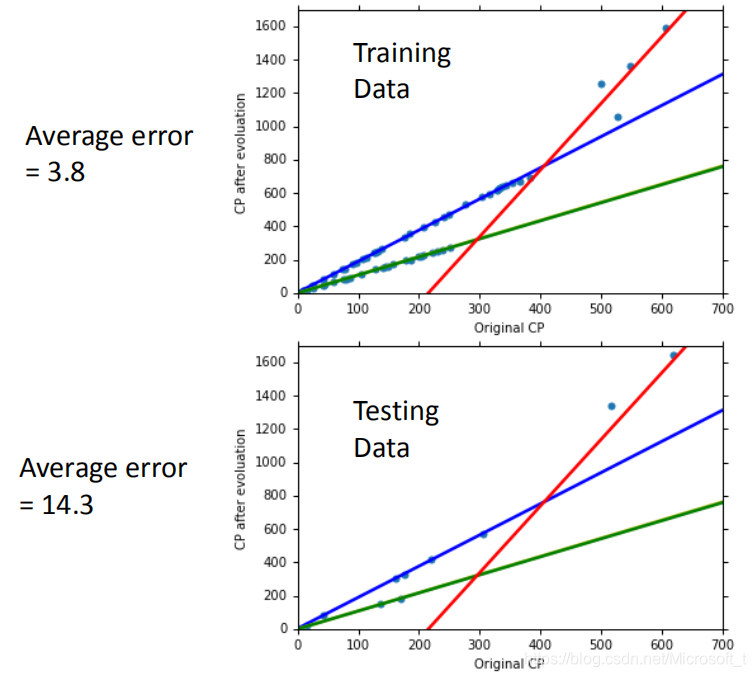
当选用一元N次模型时，训练的average error和测试的average error看似都变得更小。但是还要注意一个问题，当我们继续增加幂的次数后，将会出现过拟合问题。如下图
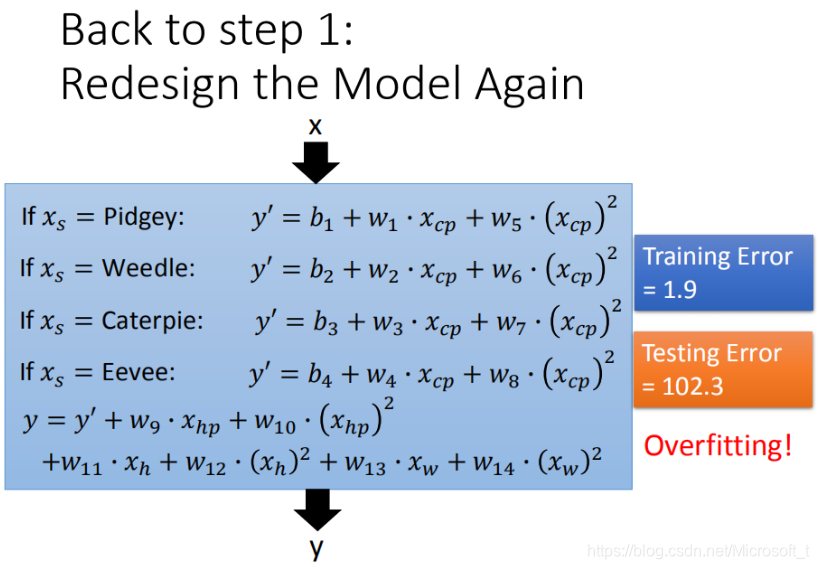
当特征量x不再唯一时，如下图
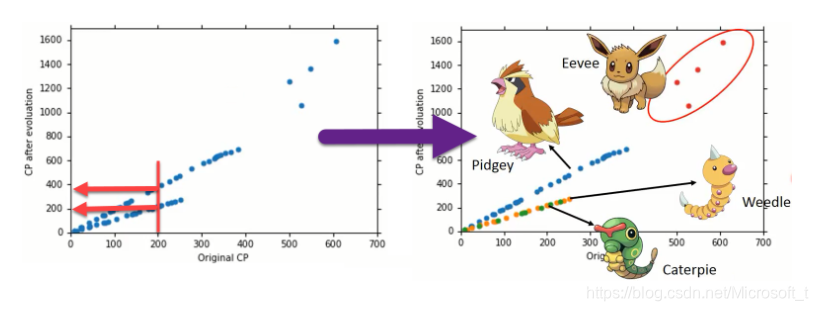
不同颜色小点，分别表示不同的物种。宝可梦的物种 不同，将对应不同的function。
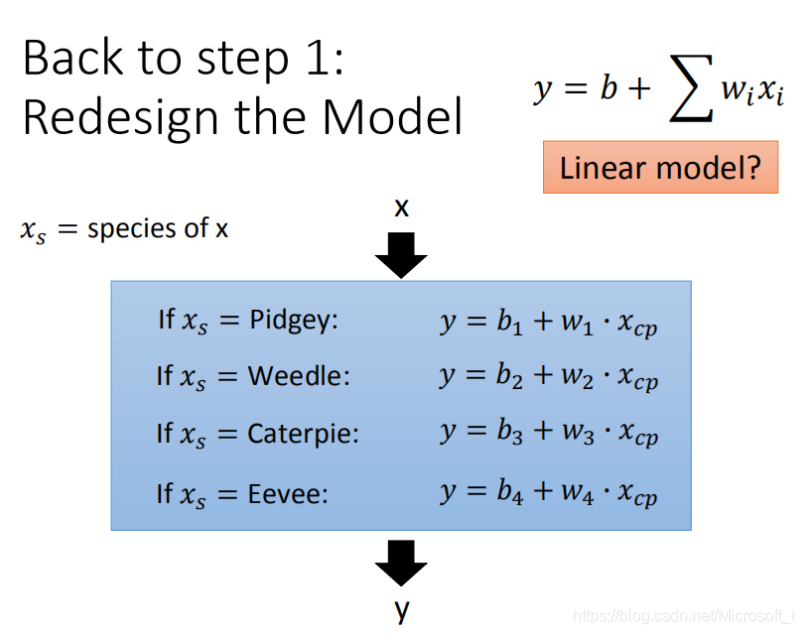
当我们学过信号与系统，将会很容易理解这个式子。假如当输入的xs（表示宝可梦物种）为喷火龙时，那么只有喷火龙的参数有效，其余都为0，这样我们就可以对不同物种进行预测了。
但是我们的特征参数不止一个，当引入参数过多时我们仍然可能导致结果过拟合。
3.正则化（regularization）
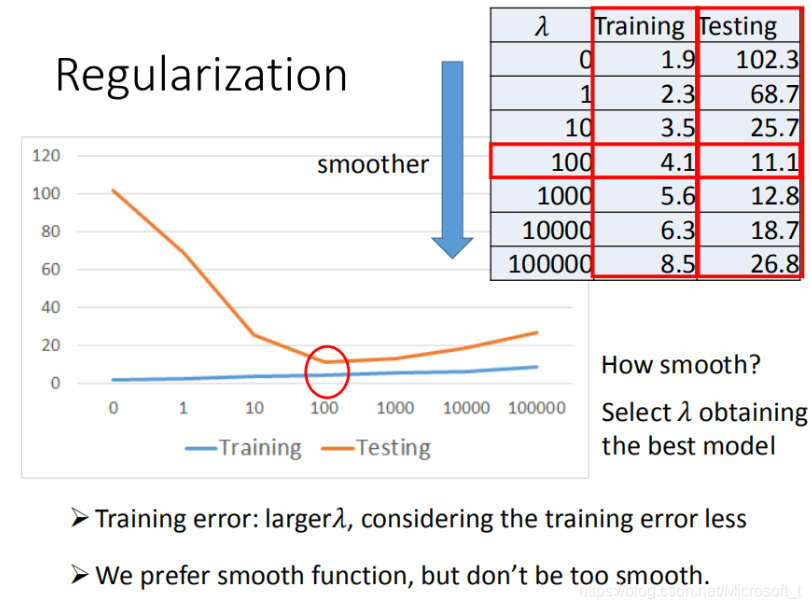
w 越小，表示function 较平滑的，function输出值与输入值相差不大
在很多应用场景中，并不是 w 越小模型越平滑越好，但是经验值告诉我们 w 越小大部分情况下都是好的。
b的值接近于0 ，对曲线平滑是没有影响