论文阅读笔记(13):Deep Comprehensive Correlation Mining for Image Clustering,用于图像聚类的深度综合相关性挖掘
来自ICCV2019的论文,源码: https://github.com/Cory-M/DCCM
摘要
最近发展的深度无监督方法允许我们共同学习表示和聚类未标记的数据。这些深度聚类方法主要关注样本之间的相关性,例如,选择高精度对来逐步调整特征表示,而忽略了其他有用的相关性。在本文中,我们提出了一种新的聚类框架,称为深度综合相关性挖掘(DCCM),用于从三个方面探索和充分利用未标记数据背后的各种相关性:
- 代替仅使用pairwise的信息,提出了伪标签监督的方法来研究类别信息和识别特征。
- 充分挖掘了特征对输入图像进行transformation的鲁棒性,有利于网络学习,显著提高了性能。
- 针对聚类问题,提出了特征间的三重互信息(triplet mutual information),将最近发现的实例级深层互信息提升到三重互信息的层次,从而有助于学习更多有判别力的(discriminative)特征。
在几个具有挑战性的数据集上进行的大量实验表明,我们的方法取得了良好的性能,例如,在CIFAR-10上实现了62.3%的聚类精度,这比最先进的结果高10.1%。
1 介绍
1.1 现状
聚类是计算机视觉和机器学习的基本任务之一。手动标记这些数据既昂贵又耗时,为了充分利用这些未标记的数据并研究它们之间的相关性,无监督聚类近年来受到了广泛的关注,其目的是基于一些相似性度量将相似的数据分类为一个聚类。
由于野生环境中图像形状和外观的变化,图像聚类是一项具有挑战性的任务。传统的聚类方法,如K-means、谱聚类和子空间聚类可能在两个主要问题上出现问题:
- 人工特征容量有限,无法动态调整以捕获先验分布,特别是在处理大规模真实图像时;
- 特征提取和聚类的分离将使解决方案次优。
最近,随着深度学习的蓬勃发展,许多研究人员将注意力转移到深度无监督特征学习和聚类,这可以很好地解决上述局限性。为了学习更好的特征表示,通常采用自动编码器最大化特征之间的互信息。DAC构建正负对来指导网络训练。
然而,对于这些方法,仍有几点遗漏:
- 只考虑重建或互信息的特征表示缺乏辨别力;
- 如k-means等传统的聚类方法有效地利用了数据的类别假设。而DAC只关注成对相关性,忽略了类别信息,这限制了其性能;
- 还有其他有助于深度图像特征学习的相关性没有考虑。
为了解决上述问题,如图1(a)所示,我们提出了一种新的方法,即深度综合相关挖掘(DCCM),该方法综合探索不同样本之间的相关性(红线)、同一样本不同层特征之间的局部粗糙度(蓝线)到几何变换(黄线)之间的相关性,以及它们之间的相互关系(绿线),以学习区分性表示并以渐进的方式训练网络。
1.2 方法介绍
- 首先,针对不同样本之间的相关性,采用深度卷积神经网络(CNN)对输入图像生成预测特征。通过添加适当的约束,学习到的预测特征将接近于one-hot的。
- 然后计算余弦相似度并构造相似度图。基于相似图(similarity graph)和预测特征,通过设定一个较大的阈值,得到高置信度 (highly-confident) 的伪图 (pseudo-graph) 和伪标签 (pseudo-graph) 用以指导特征学习。
- 为了对小扰动具有局部鲁棒性,我们在原始输入图像上加入小扰动或变换,生成变换后的图像。在局部鲁棒性假设下,变换图像的预测应与原始图像的预测一致。因此,我们可以利用原始图像的预测来指导变换图像的特征学习。
- 深层特征表示应保留输入的清晰信息。因此,我们将同一样本的深层特征和浅层特征之间的互信息最大化。为了使表示更具区分性,我们通过合并上述图形信息进一步将其扩展为三元组形式。
- 最后,我们结合这三个不同的损失函数,以端到端的方式联合挖掘这些相关性。

图1.DCCM示意图。(a)各种相关性;(b)在更高的语义层次上逐步连接pair-wise项;?在CIFAR-10上,DCCM的结果比最先进的DAC更好。
1.3 本文贡献
- 我们提出了一种新的端到端深度聚类框架,全面挖掘各种相关关系,并选择高置信度的信息进行渐进式网络训练;
- 推导了伪标签的合理性,引入了高置信度伪标签损失来直接研究类别信息,指导深度网络的无监督训练;
- 我们利用局部鲁棒性假设,并利用上述伪图和伪标签学习更好的表示;
- 我们将实例级的互信息扩展到三重态,并提出了三重态互信息损失来学习更多有鉴别力的特征。
2 相关工作
2.1 深度聚类
现有的深度聚类方法主要是将深度特征学习与传统聚类方法相结合。自动编码器(AE)是一种非常流行的深度聚类特征学习方法,人们提出了许多方法来最小化传统聚类方法的损失,以规范自动编码器潜在表示的学习。例如提出了利用KL散度损失的深度嵌入聚类(deep embedding clustering)。其它改进方法包括:使用KL散度损失但添加了一个噪声编码器,以学习更鲁棒的表示;采用k-means损失;采用基于自表达(self-representation)的子空间聚类损失。
除了自动编码器外,有些方法直接根据最后一层输出设计特定的损耗函数引入了一个循环聚集框架来合并彼此接近的聚类。有些方法 基于标签特征探索不同样本之间的相关性,并使用相似性作为监督将谱聚类扩展到深层公式中。
2.2 深度无监督特征学习
有几种方法主要关注表征的深度无监督学习,而不是聚类。[13]基于生成性对抗网络(GAN),建议添加编码器以提取视觉特征;[4] 直接使用从单位球体均匀采样的固定目标来约束深度特征分配;[8] 利用k-means对输出特征计算的伪标签作为监督训练深层神经网络;[23]提出了deep-infomax以最大化深度神经网络的编码器输入和输出之间的互信息。
2.3 自监督学习
自监督学习通常需要设计一个代理任务(pretext task),在这个任务中,可以在没有监督的情况下计算target的目标函数。他们假设代理任务学习到的表示能够包含高级语义信息,这些信息将有助于解决关注的下游任务,如图像分类。例如,[12]尝试预测图像块的相对位置;[39,40]预测从完整图像创建的拼图的排列;[15]将每个图像视为一个单独的类,并通过数据增强生成多个图像以训练网络;[19]将图像随机旋转四个不同角度中的一个,并让深度模型预测是哪种旋转。
3. DCCM
没有标签,数据本身的相关性在深度聚类中最为重要。
在这一部分中,我们首先构造伪图来探索样本之间的二值相关性,从而开始网络训练。为了充分利用数据背后的类别信息,我们提出了伪标签损失算法。接下来,我们挖掘在输入图像上添加变换前后预测的局部鲁棒性。我们还将实例级互信息提升到三重态级别,以使其更具区分性。最后,我们将它们结合起来,得到我们提出的方法。
3.1 伪图监督
我们首先计算样本之间的相似度,并通过构造伪图来选择高置信度的pair-wise信息来指导网络训练。令 X = { X i } i = 1 n \mathcal X=\{X_i\}_{i=1}^n X={Xi?}i=1n?为未标记数据集,其中 x i x_i xi?是第 i i i个图像,N是图像的总数。 K K K为类的总数。我们的目标是学习一个基于深度CNN的、由 θ θ θ参数化的映射函数 f f f,那么可以用 z i = f θ ( x i ) ∈ R K z_i=f_θ(x_i)∈\mathbb R^K zi?=fθ?(xi?)∈RK表示CNN经过Softmax层后对图像 x i x_i xi?的预测结果。它具有以下特性:
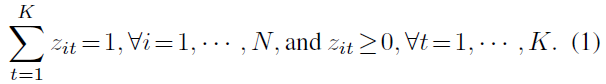
基于标签特征z,第i个样本和第j个样本之间的余弦相似性可以通过计算
S
i
j
S_ij
Si?j得到:
S i j = z i ? z j ∣ ∣ z j ∣ ∣ 2 ∣ ∣ z i ∣ ∣ 2 S_ij=\frac{\textbf z_i\cdot \textbf z_j}{\vert\vert \textbf z_j \vert\vert_2 \vert\vert \textbf z_i\vert\vert_2} Si?j=∣∣zj?∣∣2?∣∣zi?∣∣2?zi??zj??
与DAC类似,我们可以通过设置大阈值
t
h
r
e
s
1
thres_1
thres1?来构造伪图
W
W
W:
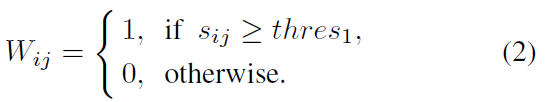
如果两个样本之间的相似性大于阈值,则我们判断这两个样本属于同一类
W
i
j
=
1
W_{ij}=1
Wij?=1,并且这些样本的相似性应最大化。否则
W
i
j
=
0
W_{ij}=0
Wij?=0,这些样本的相似性应最小化。伪图的监督可定义为:
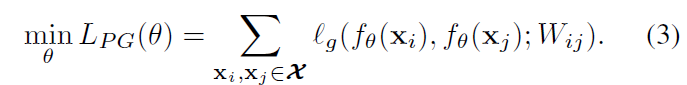
PG即伪图pseudo-graph缩写。其中对于损失函数 ? g \ell_g ?g?可以有许多选择,如对比Siamese网络损失调整两个样本之间的距离,以及二元交叉熵 (BCE) 损失调整相似性
请注意,我们的伪图与DAC的伪图有两个不同之处:
-
DAC中使用了强 ? 2 \ell_2 ?2?范数约束,而我们relax了这种假设,只需要对数据进行softmax。这种relax增加了标记特征的能力,最终在我们的实验中得到了更好的结果。
-
我们不需要在DAC中动态降低阈值,而只需要固定的阈值 t h r e s 1 thres1 thres1。这避免了训练中噪声假阳对(false positive pairs)带来的不利影响。
3.2 伪标签监督
伪图中的相关性是不可传递的,并且仅限于成对样本。针对这一问题,在本小节中,我们提出了一种新的伪标签损失算法,并证明了其合理性。我们首先证明了伪图的K-分割的存在,它可以被自然地看作是伪标签。然后我们声明这个划分将得到式(3)中的最优解 θ ? θ^? θ?,这是一个one-hot预测,从而形成伪标签。最后,引入伪标签损失对卷积神经网络进行优化。
K-分割的存在性
在方程(3)中定义的样本 x i x_i xi?和 x j x_j xj?之间的二值相关性 W i j W_{ij} Wij?是不可传递的:给定的 W i k W_{ik} Wik?和 W j k W_{jk} Wjk?并不能让我们确定 W i j W_{ij} Wij?,这可能导致训练不稳定。因此,引理1将其推广到更强的关系。
引理1
对任意加权完全图(weighted complete graph)
G
=
(
V
,
E
)
G=(V,E)
G=(V,E),其边
e
e
e的权重为
w
(
e
)
w(e)
w(e)。若对所有
i
≠
j
i\neq j
i?=j都有
w
(
e
i
)
≠
w
(
e
j
)
w(e_i)\neq w(e_j)
w(ei?)?=w(ej?),那么存在一个阈值
t
t
t使得
G
t
(
V
,
E
t
)
G_t(V,E_t)
Gt?(V,Et?)存在K-分割。其中
E
t
E_t
Et?为:
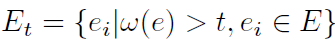
如果我们假设相似图S中的
S
i
j
S_ij
Si?j是区别于其它元素的的,那么根据在引理(1),它可以看作是一个加权完全图。然后存在一个阈值t将
X
X
X精确地划分为K个partition
{
P
1
,
P
2
,
?
?
,
P
K
}
\{P^1,P^2,\cdots,P^K\}
{P1,P2,?,PK}。
伪标签公式
设 x k x^k xk表示样本属于分区 P K P^K PK,我们可以定义传递关系 δ δ δ为:
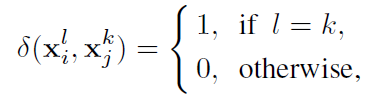
同分区传递,不同分区分割
这表明具有高余弦相似性的对保证在同一分区中。也就是说,随着训练过程中相似度矩阵S质量的提高,该划分更接近于ground truth划分,因此可以作为指导和加速训练的目标。因此,我们将每个 x x x所属的分区 k k k作为伪标签。
以下论述揭示了分配的伪标签与softmax之后的预测结果之间的关系:
论述1
令
θ
?
\theta ^*
θ?为公式(3)的最优解,如果W有K分割,那么预测结果应当是one-hot的:
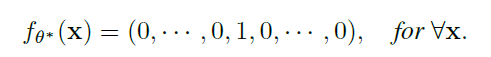
因此,我们可以将伪标签表述为:
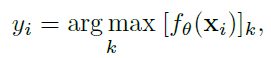
其中, [ ? ] k [·]_k [?]k?表示预测向量的第k分量。其对应的预测伪标签概率可通过 p i = m a x [ f θ ( x i ) ] k p_i=max[f_θ(x_i)]_k pi?=max[fθ?(xi?)]k?计算。实际上, f θ ( x i ) f_θ(x_i) fθ?(xi?)并不严格遵循one-hot性质,因为由于非凸性质,很难获得方程(3)中问题的最优解。因此,我们还为概率 p i p_i pi?设置了一个较大的阈值 t h r e s 2 thres_2 thres2?,以选择高度可靠的伪标签进行监督:
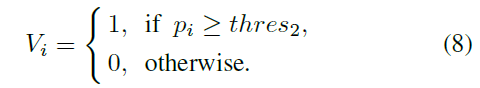
V
i
=
1
V_i=1
Vi?=1表示预测的伪标签是高置信度的,并且只有在这种情况下,第
i
i
i个样本的伪标签
y
i
y_i
yi?才会加入监督训练。
伪标签损失
用伪标签来监督的损失函数如下:
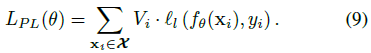
其中
?
1
\ell_1
?1?通常使用交叉熵损失。通过结合高置信度伪图和伪标签的监督,我们最小化:
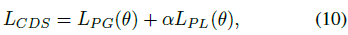
这些被挑选出来的高置信度伪的信息能够以渐进的方式监督深度网络的训练。
3.3 局部鲁棒性
理想的图像表示应该具有对几何变换保持的不变性,这可以看作局部鲁棒性假设。在数学上,给定一个图像样本 x x x和一个几何变换 G G G, x ′ = G ? x x' = G·x x′=G?x为变换样本,那么一个好的特征提取器 f θ f_θ fθ?应该使这两个样本具有相同的标签,且 f θ ( x ) ≈ f θ ( x ′ ) f_θ(x)≈ f_θ(x') fθ?(x)≈fθ?(x′) 因此我们可以把 f θ ( x ) f_θ(x) fθ?(x)和 f θ ( x ′ ) f_θ(x') fθ?(x′) 之间的距离作为特征不变性损失:
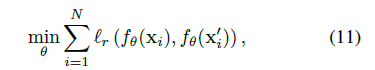
?
r
\ell_r
?r?是
?
2
\ell_2
?2?-范数,用于测量原始样本和transform后样本的预测结果之间的距离。转换产生的
x
x
x和
G
?
x
G·x
G?x可以看作是“易正例对”,可以很好地稳定训练。
此外,请记住,对于原始样本,我们计算伪图和伪标签作为监督。我们希望基于transform样本计算的图形和标签信息应与原始样本的图形和标签信息一致,而不是简单地最小化预测距离。所以需要对伪图和伪标签的距离都最小化:
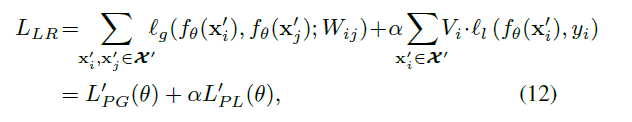
深度无监督学习可以从上述策略中受益匪浅。由于我们对伪图和伪标签的构造设定了较高的置信度,因此可以将其视为简单的样本,导致这对参数学习几乎没有贡献。通过加入小扰动,变换样本的预测将不像原始样本那样容易,这将有很大的回报。
3.4 三重互信息 Triplet Mutual Information
在本节中,我们探讨了每个实例的深层和浅层表示之间的相关性,并提出了一种新的损失,称为三重互信息损失,以充分利用特征对应信息。
同一样本的深层和浅层特征之间的互信息(MI)应最大化,以保证表示的一致性。与[41]类似,我们还将两个随机变量(D和S)的MI转换为来自联合分布 J \mathbb J J的样本与其边缘 M \mathbb M M的产量之间的Jensen-Shannon散度(JSD)。相应地,不同层次的特征只有当它们是同一样本的特征时才应该遵循联合分布,否则,它们遵循边际产量(Marginal product)分布。因此,JSD版本MI定义为:
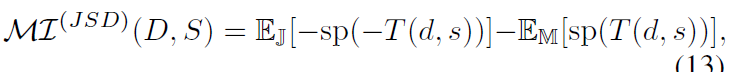
其中,
d
d
d对应于深层(deep)特征,
s
s
s对应于浅层(shallow)特征,
T
T
T是经过训练以区分
d
d
d和
s
s
s是否从联合分布中采样的鉴别器,
s
p
(
z
)
=
l
o
g
(
1
+
e
z
)
sp(z)=log(1+e^z)
sp(z)=log(1+ez)是softplus函数。对于鉴别器实现,在输入中加入关于局部性的知识可以提高表示的质量。
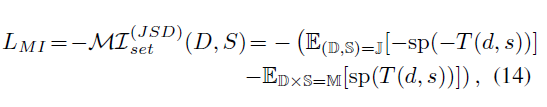
请注意,目前,我们没有纳入任何类别信息。对于两个不同的样本 x 1 x_1 x1?和 x 2 x_2 x2?,即使它们属于同一类别, x 1 x_1 x1?的浅层表示和 x 2 x_2 x2?的深层表示之间的互信息将最小化,这是不合理的。因此,我们考虑通过引入正对的互信息损失来解决这个问题。如图2右下角所示,使用第3.1节中描述的生成伪图W,我们选择具有相同锚定的正对和负对来构造三重态关联。与监督学习类似,该方法将实例级互信息监督提升为三层监督。

图2.拟议DCCM方法。基于理想的one-hot预测特征,我们计算高置信度伪图和伪标签来指导原始样本和变换样本的特征学习(右上角),研究不同样本之间的相关性和小扰动后的局部鲁棒性(左)。同时,为了研究区分性特征对应,利用伪图选择高置信度的正负对进行三重互信息优化(右下角)。
3.5 联合优化
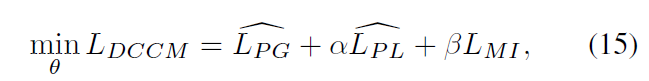
非常浅显:
m
i
n
θ
L
D
C
C
M
=
(
L
P
G
+
α
L
P
L
)
(
伪
图
伪
标
签
监
督
)
+
(
L
P
G
′
+
α
L
P
L
′
)
(
局
部
鲁
棒
性
监
督
)
+
β
L
M
I
(
三
重
互
信
息
)
min_\theta L_{DCCM}=(L_{PG}+\alpha L_{PL})(伪图伪标签监督)+(L'_{PG}+\alpha L'_{PL})(局部鲁棒性监督)+\beta L_{MI}(三重互信息)
minθ?LDCCM?=(LPG?+αLPL?)(伪图伪标签监督)+(LPG′?+αLPL′?)(局部鲁棒性监督)+βLMI?(三重互信息)
我们提出的方法可以以基于小批量的端到端方式进行训练,可以有效地进行优化。在训练之后,预测的特征在理想情况下是one-hot的。通过计算公式7,样本
x
i
x_i
xi?预测的聚类标签与伪标签
Y
i
Y_i
Yi?完全相同。我们在算法1中总结了整个训练过程。

4 实验
我们把实验分成几个部分。我们首先通过将DCCM与其他最先进的算法进行比较来检验DCCM的有效性。之后,我们通过控制几个影响因素进行更多的消融研究。最后,我们做了一系列的分析实验来验证统一模型训练框架的有效性。
数据集
对于聚类任务,我们联合使用每个数据集的训练和验证图像,并将这些图像调整为96×96×3。
对于迁移学习分类任务,训练和测试样本是分开的。
评价指标
为了评估聚类性能,我们采用了三种常用的指标,包括归一化互信息(NMI)、准确度(ACC)、调整rand指数(ARI)。这三个指标有利于聚类任务中不同的属性。对于所有三个指标,值越高表示性能越好。
为了评估特征表示的质量,我们采用了非线性分类任务。具体地说,在DCCM训练之后,我们固定了深度神经网络的参数,并分别在最后一个卷积层和全连接层特征的的顶层,以有监督的方式训练了一个具有单隐藏层(200个单元)的多层感知网络。
实施细节
我们框架中使用的网络架构是AlexNet的浅版本。我们采用lr=1e-4的RMS-prop优化。对于超参数,我们为所有数据集设置了
α
=
5
α=5
α=5和
β
=
0.1
β=0.1
β=0.1。构造高置信度伪图和伪标签的阈值分别设置为
0.95
0.95
0.95和
0.9
0.9
0.9。实验中使用的小扰动包括旋转、移位、重缩放等。对于互信息估计的鉴别器,我们采用三个1×1卷积的网络。
4.1 可视化
图3显示了使用t-SNE在CIFAR-10上嵌入DCCM和DAC的特征[36]。我们可以看到,与DAC相比,DCCM表现出更具区别性的特征表示。以上结果充分验证了我们提出的DCCM的有效性和优越性。

为了进一步评估特征表示的质量,我们采用了分类任务,并将DCCM与其他深度无监督特征学习方法进行了比较。图4显示了各个方法的top-1非线性分类精度。我们还可以观察到,在CIFAR-10和CIFAR-100数据集上,DCCM比其他方法取得了更好的结果。特别是在CIFAR-10数据集上,我们对卷积和完全连接层特征的结果比第二好方法DIM的结果高出8%以上。

4.2 消融分析
本节从局部稳健性、伪标记和三重态互信息三个方面分析了各种相关性的有效性。结果如表3所示。

局部鲁棒性
方法M2和M1之间的唯一区别在于是否使用局部鲁棒机制。我们可以看到M2显著优于M1,这表明了局部鲁棒性的鲁棒性和有效性。由于我们设置了高阈值来选择正对,这对参数学习的贡献有限。在局部鲁棒性损失的情况下,我们构造了许多难样本对以利于网络训练。因此,它显著提高了性能。
伪标签的有效性
在伪标签的帮助下,M3(同时使用伪图和伪标签)在所有度量下都比M2(仅使用伪图)获得更好的结果。这是因为伪标签可以充分利用特征分布背后的类别信息,有利于聚类。
三重互信息分析
正如我们在第3.4节中所分析的,借助伪图,三重态互信息不仅可以利用同一样本的特征对应,还可以通过构造正负对引入鉴别性质。因此,它可以进一步改善结果。
4.3 DCCM的总体研究
伪图的BCubed精度和召回率
BCubed是评估聚类中分割质量的指标。我们验证了我们的方法可以通过使用基于图5中不同时期的伪图计算的BCubed精度和召回曲线以渐进方式学习更好的表示。很明显,随着时期的增加,伪图的精度变得更好,这将反过来提高聚类性能。

预测特征
根据之前的分析,理想的预测特征是one-hot的,因此我们可以使用高置信度的伪标签来指导训练。为了验证这一点,我们比较了初始阶段和最终阶段之间最大预测概率的分布,结果如图6(a)所示。
阈值的影响
在图6(b)中,我们测试了阈值对选择高置信度伪标签进行训练的影响。我们可以看到,随着阈值的增加,性能也随之提高。这是因为在低阈值的情况下,网络训练会采用一些不正确的伪标签,这会影响性能。
