[人工智能][2021-ICCV] MUSIQ Multi-scale Image Quality Transformer

[2021-ICCV] MUSIQ: Multi-scale Image Quality Transformer

论文：https://arxiv.org/abs/2108.05997

代码：https://github.com/google-research/google-research/tree/master/musiq

概述

当前SOTA的IQA（图像质量评估）模型都是基于CNN的，基于CNN的模型通常受到在一个批次内，图像尺寸必须固定的限制，所以其输入图像通常会进行缩放或者裁剪，当然这会导致图像质量的下降。为了解决这个问题，本文设计了一个多尺度的图像质量transformer（multi-scale image quality transformer）来处理不同尺寸、不同长宽比的原分辨率图像。通过多尺度的图像表示，本文的模型可以捕捉到不同粒度（granularity）的图像质量。另外，本文提出了一种新型的基于哈希的（hash-based）二维空间嵌入方法和一种尺度嵌入，来作为多尺度表示中的位置嵌入。

上图中右侧(b)图是传统的CNN模型的做法，必须要缩放或者裁剪来固定输入图像尺寸，而这无疑会影响原图的图像质量；而左侧(a)图则是本文的多尺度图像质量transformer，基于图像块可以以多尺度的形式直接处理原图。

另外，由于MUSIQ只改变输入编码，因此它可以适应任何transformer变体，也就是说，本文提出的创新点是在编码阶段的处理方法，得到输入编码之后可以放到Swin、CvT之类的新型transformer里都是可以的。

本文的创新点总结如下：

1. 本文提出一种基于图像块的多尺度图像质量transformer（multi-scale image quality transformer MUSIQ），可以处理不同尺寸、不同长宽比的全尺寸输入图像，并且可以提取多尺度的特征。
2. 本文提出了一种新型的基于哈希的（hash-based）二维空间嵌入方法和一种尺度嵌入，来帮助transformer捕获空间间和尺度间的信息。
3. 本文提出的MUSIQ在四个大规模IQA数据集上取得SOTA性能。

方法

模型框架

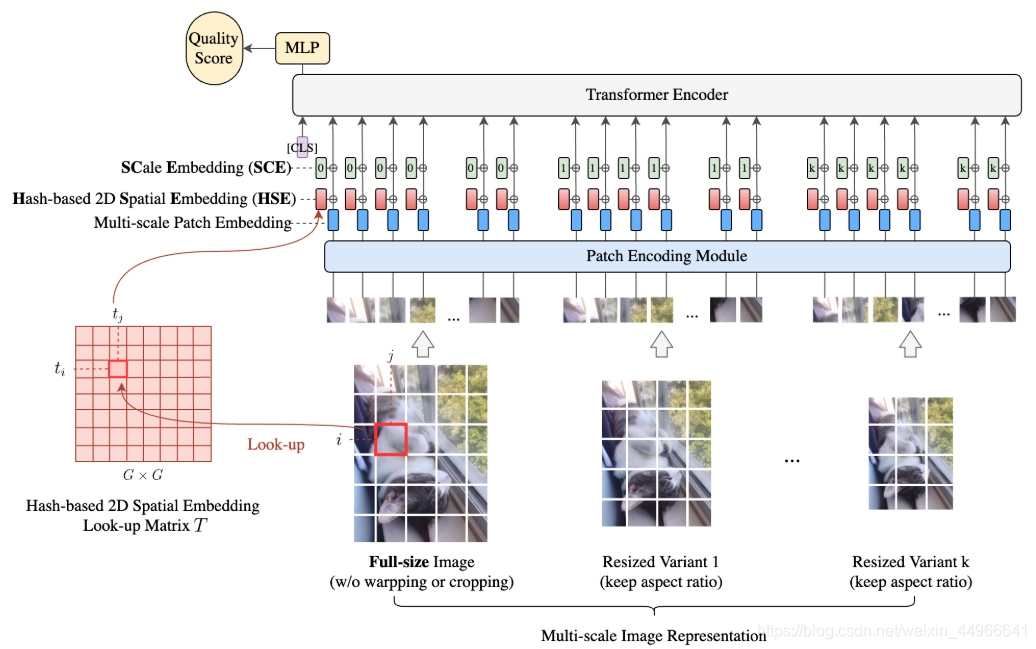
MUSIQ的整体结构如上图所示，首先得到输入图像的多尺度表示，包括原图和固定长宽比缩放（ARP(aspect ratio preserved) resized）的变体。不同尺度的图像被分成固定大小的图像块，然后被送入到模型中，由于图像块是来自不同的空间分辨率的图像，我们需要高效地将这些多种长宽比、多种尺度的输入编码为一个token序列，捕获像素、空间和尺度信息。

为此，本文设计了三个编码模块：

1. 图像块编码模块
2. 基于哈希的空间嵌入模块
3. 可学习的尺度嵌入

分别对来自多尺度图像的图像块本身、每个图像块的二维空间位置、不同的尺度进行编码。

在将多尺度的图像输入编码为一个token序列之后，我们先准备一个额外的可学习的分类头classification head（CLS）。transformer encoder输出中的CLS token将作为最终的图像表示。然后在最后加一个全连接层来预测图像质量分。由于MUSIQ只改变输入编码，因此它可以适应任何transformer变体，也就是说，本文提出的创新点是在编码阶段的处理方法，得到输入编码之后可以放到Swin、CvT之类的新型transformer里都是可以的。

多尺度图像块嵌入

ARP resize = aspect ratio preserved resize 即固定长宽比缩放，后面不在赘述，直接简称ARP resize。

为了同时捕获局部信息和全局信息（各种多尺度方法的老说辞了^^），本文提出对图像的多尺度表示进行建模。

记全尺寸原图的高、宽、通道书分别为 $H,W,C$， 使用高斯核对全尺寸原图进行ARP resize（保持长宽比的缩放）之后的多尺度图像的高、宽、通道数分别为 $h_k,w_k,C$ ，其中 $k=1,\dots ,K$ ，$K$是每个输入的ARP resize变体的个数。为了将多尺度输入对齐，从而有一致的全局视角，将每个多尺度辩题的长边固定为 $L_k$ ，从而：
$${\alpha }_k=L_k/max(H,W),h_k={\alpha }_{k}H,w_k={\alpha }_{k}W$$
${\alpha }_k$ 即为每个尺度的缩放因子。

从每个多尺度图像中切分出尺寸为 $P$ 的正方形图像块。对于高、宽不是 $P$ 的整数倍的图像，用零填充（这里笔者有个问题：既然都padding 0了，那不就相当于也将输入的尺寸固定了吗，既然可以padding，那什么网络都能处理原尺寸图像啊，没搞懂这样设计还有什么意义）。每个图像块被图像块编码器模块patch encoder module编码为 $D$ 维的嵌入，$D$? 即为transformer中的隐层token尺寸。本文的patch encoder module使用了5层的ResNet而非线性映射。将patch encoder module输出的图像块嵌入拼接起来就得到输入图像的多尺度映射序列，来自原尺寸图像和ARP resize的多尺度图像的图像块个数就分别为：$N=HW/P^2$，$n_k=h_k{w}_k/P^2$ 。

对于输入图像尺寸不同导致的 $N,n_k$ 不同，从而序列长度不同的问题。本文采用了NLP中常用的pad+mask的方式来得到固定长度的输入，从而进行训练。前面提到过ARP resize图像的长边固定在 $L_k$? ，因此有 $n_k<=L_k^2/P^2=m_k$ ，所以直接pad到 $m_k$ 即可。

基于哈希的二维空间嵌入

传统的固定长度的位置嵌入无法适应可变分辨率的输入，并且也无法对齐来自不同尺度但空间位置接近的图像块。

本文认为一个有效地适合MUSIQ的位置嵌入应当满足以下条件：

1. 可以在不同长宽比、不同分辨率下有效地为图像块的空间信息进行编码；
2. 不同尺度下空间位置接近的图像块应当有相近的空间嵌入
3. 便于实现，不会干扰到transformer attention

据此，本文提出了一种基于哈希的二维空间嵌入（HSE），记某个图像块的位置在第 $i$ 行，第 $j$ 列，被哈希到 $G\times G$ 的网格中的相应的元素。该网格中的每一个元素是一个 $D$ 维的嵌入向量。即有一个可学习的矩阵 $T\in {\mathbb{R}}^{G\times G\times D}$ ，输入尺寸为 $H,W$ ，对于位置在 $(i,j)$ 的图像块，其空间嵌入被定义为 $T$ 中的 $(t_i,t_j)$ 位置的元素：
$$t_i=\frac{i\times G}{H/P},t_j=\frac{j\times G}{W/P}$$
将 $D$ 维的空间嵌入 $T_{t_i,t_j}$ 逐元素地加到patch embedding上。为了快速查找，将$(t_i，t_j)$四舍五入到最接近的整数。

为了在不同尺度之间对齐图像块，来自不同尺度的图像块都映射到一个同样的表格 $T$。这样，在空间上位置接近但是来自不同的尺度的图像块也会被映射到$T$中接近的嵌入上。因为$i$和$H$以及$j$和$W$与尺寸调整因子$\alpha$成比例变化。

$T$ 的尺寸 $G$ 存在一个trade-off，$G$? 过小会导致过多的哈希碰撞，从而使得模型无法分辨空间位置接近的图像块；过大则会导致浪费内存并且需要更多的分辨率来进行训练。

尺度嵌入

由于本文对所用的图像复用一个相同的哈希矩阵，HSE是无法分别来自不同尺度的图像块的，因此本文引入一个额外的尺度嵌入SCE来帮助模型分辨来自不同尺度的图像块。

本文将SCE定义为一个可学习的嵌入 $Q\in {\mathbb{R}}^{(K+1)\times D}$ ，因为输入有 $K$ 个尺度的变体。$Q_0\in {\mathbb{R}}^D$ 逐元素地加到所有的 $D$ 维的原分辨率图像的pathch embedding上，$Q_k\in {\mathbb{R}}^D$ 分别逐元素地加到所有 $k$ 尺度的patch embedding上。

预训练和微调

本文预训练还是在ImageNet上做的，预训练阶段会使用各种数据增广的方法来提升性能。

微调则是在图像质量和美学质量数据集上进行，在微调阶段，保持原尺寸图像作为输入，数据增广只采用对图像质量无影响的水平翻转。

本文的概述和方法就简单地介绍到这里，已经囊括方法思路和大部分细节，对实验有兴趣的话请到原文中自行查看。