引言

从2016年AalphGO横空出世，惊艳众人到现在2021世界魔幻，吴签大碗牢饭已经4年多时间，这四年是机器学习，深度学习的AI智能算法蓬勃兴盛的4年，未来怎么样，大佬们各有分说，作为普通人，还是好好踏踏实实抓住潮流提升自己，才是应对这魔幻世界的真道理。笔者今年研一，从本科搞前端到现在转型搞智能，痛苦与快乐并行，今天这篇文章作为之后转型开始的处女之作，感谢各位赏光垂阅拙作。

今天这篇文章以线性回归为例，带领读者入门机器学习领域，机器学习是AI领域的一个子范畴，所有可以实现机器自学习的算法都属于这个领域，但是就目前发展来看，机器学习方法论有一套成熟的流程体系，也即是“学习”的含义，是机器模拟人类进行学习的过程。

机器学习是一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。 ———— 引自《百度百科》

区分有监督和无监督任务

机器学习将学习任务中的数据是否经过了人工标注作为有监督或无监督的标准。举个例子，如果我们想根据一个人的身高体重来判断这个人是属于瘦还是胖，那么我们人类先得告诉机器什么样的身高体重属于瘦或者胖，这显然属于有监督的任务；如果我们想根据一个班级中学生的性格指标给学生分成几组，那么显然我们人类并不会直接告诉机器应该怎么分组，而是让机器通过算法自己建立一个分组，这属于无监督任务。一般来说，有监督学习的应用场景是要远大于无监督的应用场景的。

区分回归问题与分类问题

在机器学习领域，几乎所有的有监督问题都被划分为了回归和分类问题。所以，在进入机器学习领域中的第一件事情是要学会区分要解决的问题是分类还是回归。从通俗意义上讲，分类是识别谁是谁的问题，而回归是预测谁有多少的问题。比如，对于一张猫或狗的照片，要分辨到底是猫还是狗，这属于分类问题；对于根据几个月的销售情况预测下一个月的销售额，这属于回归问题。但是有些时候，一个实际问题的定义没有那么明显的分类或预测含义，这个时候就需要看数据的Label是连续的，还是离散的，如果是连续的就是回归问题，离散的就是分类问题。

线性回归问题

了解了一些机器学习中的基本概念，我们来看看什么是线性回归问题。形如：
$\theta_0 + \sum_{i=1}^{n}\theta_ix_i \newline given\ \ y,x_i(i=1,2,...,n) \newline solve\ \ \theta_j(j=0,1,2,...,n)$
这类均属于线性回归问题，之所以称之为线性，是因为 $y$ 是 $x$ 的线性组合。考虑一下线性回归问题属于有监督还是无监督？显然属于有监督，因为不仅有 $x$ ，还有 $y$ ，我们告诉了模型应该具有怎么样的输入和输出，让模型通过学习得到一组 $\theta$ ，使得满足这样的输入输出。举个例子，比如对于全国的商品房样本我们知道其三个维度的信息：所在城市( $x_1$ )，所在区域的人口密度( $x_2$ )，所在区域的中小学数目( $x_3$ )，以及这个商品房的价格( $y$ )，请你用线性回归建模问题并求解模型参数。

从传统算法到基于统计的机器学习算法

当你考虑解决上述线性回归问题时，你会发现我们很难从已有的传统算法思想（例如，分治，动态规划，贪心等）中找到一个适合解决这个问题的思想。因为往往来说，传统算法思想适用于找精确解，但是这个问题的精确解很难求出来，就比如房价的预测涉及到方方面面的因素，因素的作用有大有小，即便是经验老道的内行去预测也会有所偏差，所以在机器学习领域，我们找到的解往往是近似解。求解近似解的方法，也可以使用基于一定启发式规则的算法求解，但是当数据量巨大时，这种方法的效果就有些捉襟见肘，这也就是近年来机器学习与深度学习蓬勃发展的原因，数据流量激增的时代，从数据中挖掘潜在价值是这些AI算法的使命。

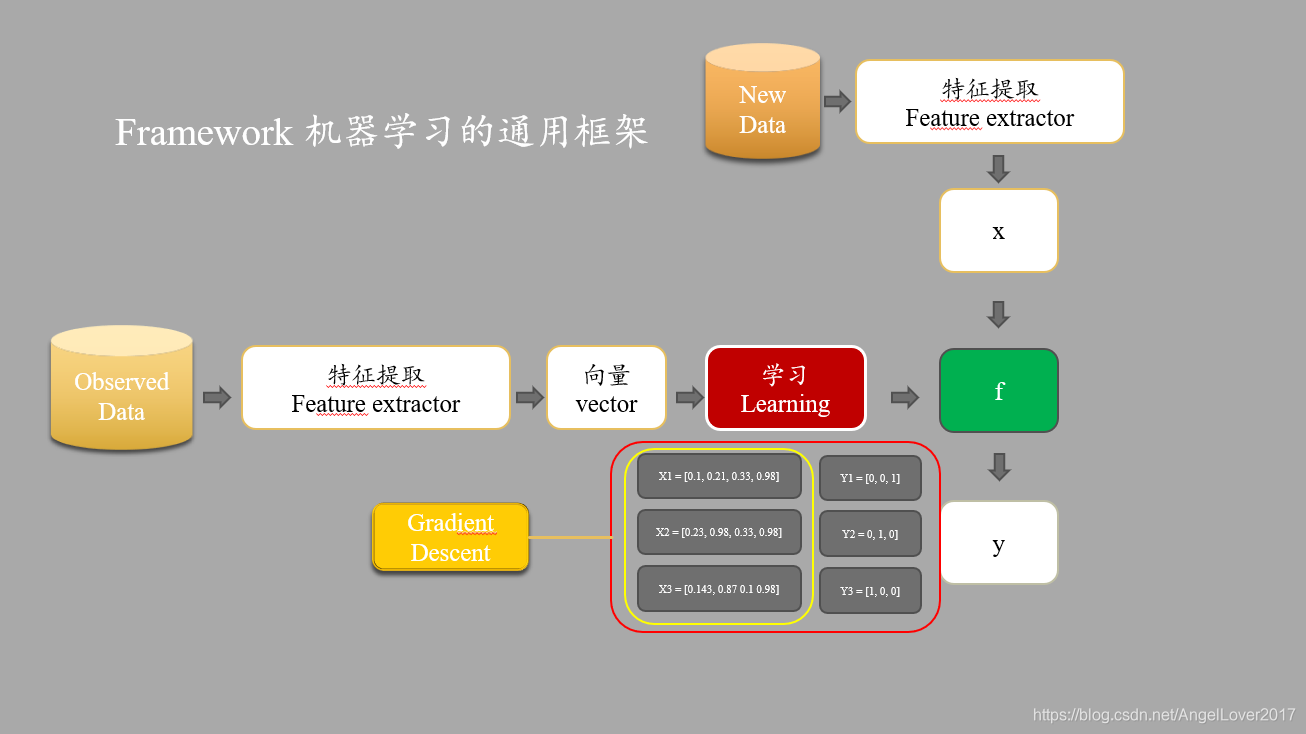
机器学习的通用框架可以简单理解为四个部分：特征提取，向量化表征，训练学习，梯度下降。

特征提取：从一堆因素中提取出对模型影响更大的一些特征。例如，房价预测中影响房价的因素很多，但是并不是所有的因素都是有用的，可能存在噪声因素，我们必须在模型学习前剔除这些因素。
向量化表征：我们收集来的数据很大程度上不完全是数值类型的，很多可能是字符串表示。基于统计的机器学习算法，只认识数值，因此我们需要用数值表征特征，一个特征的一组数值就是一个向量。
训练学习：训练学习是将数据不断送入模型，模型经过多轮学习，不断调整参数( $\theta$ )的过程。
梯度下降：严格意义上讲，梯度下降属于训练学习范畴，是训练学习不断迭代的核心所在。如果读者学习过凸优化理论，可能会知道，这是求解优化问题的最简单的迭代方法。

实战部分

我们接下来将以一个简单的线性回归例子，来讲述一个完整的机器学习过程。

数据生成

现在，假设我们有一组( $x, y$ )数据，要使用线性回归来建模并求解。我们先来为接下来的例子生成一点数据。我们按照如下公式进行数据生成：
$5x+100+\theta_{random} \newline x = 0,1,...,99 \newline \theta_{random}\in\{\theta|-100\leq\theta\leq100\}$

import random
import numpy as np
import matplotlib.pyplot as plt
def gf(a,b):
    def f_(x):
        return a*x + b
    return f_
def generate_data(count,f_args=(3,4)):
    x = np.arange(count)
    f = gf(*f_args) 
    y = f(x) + np.array([random.randint(-100,100) for i in range(count)]) 
    return (y,x)
y,x = generate_data(100,(5,100))
plt.scatter(x,y)

绘制出来的散点图如下所示：
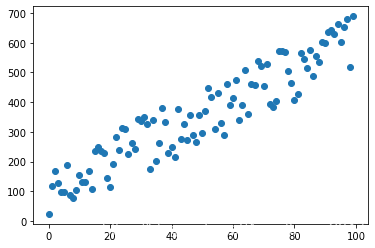
在这里插入图片描述
在这个例子中，我们忽略了特征提取和向量化，因为我们生成的数据直接就是可以输送给模型的向量( $\vec{x},\vec{y}$ )。

建模与求解思路

线性模型

很显然，在这个例子中，我们期望的模型就是 $y = 5 x + 100$ ，但是我们希望机器可能自己学习得到，因此首先建立一个线性模型：
$h_\theta(x) = \theta_0 + \theta_1x \newline$

损失函数

有了模型，我们还需要一个评价模型好坏的指标，怎么知道模型能够很好的拟合上面这些点的分布呢？在回归问题中，我们常用的最为简单的评价指标就是MSE(均方误差函数)：
$J(\theta_0,\theta_1) = \frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2$
这里之所以是 $\frac{1}{2m}$ ，而不是 $\frac{1}{m}$ 的原因是，为了修正MSE求导后的多出来的系数 $2$ 。这里的评价指标函数也常常被称之为Loss函数，或者Cost函数。事实上，这个指标衡量了真实值( $y$ )与模型给出的预测值( $h_\theta(x)$ )直接的平均误差。很容易理解，我们希望这个误差越小越好，因为越小就表示我们的模型更能贴近真实的数据。

def MSE_Loss(x,y,fn):
    m = len(x)
    y_hat = fn(x)
    loss = (1/(2*m)) * (np.sum((y_hat-y)**2))
    return loss

梯度下降

所以，我们很容易利用凸优化理论，将这个问题转换为一个优化问题。
$\theta^* = arg\ \mathop{min}\limits_{\theta} J(\theta) , \theta = [\theta_0,\theta_1]^T$
求解这个优化问题，可以使用梯度下降方法，梯度下降公式如下：
$\theta^{n} = \theta^{n-1} - \alpha\frac{\partial J(\theta^{n-1})}{\partial\theta^{n-1}}$
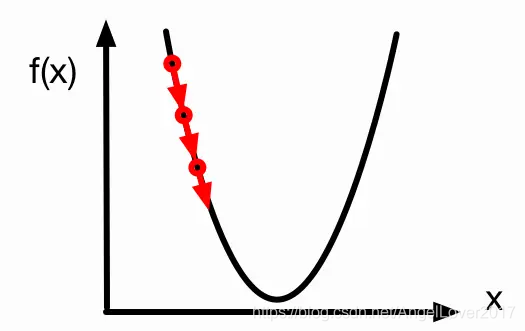
我们可以简单理解一下梯度下降的真实含义。 $\alpha$ 代表就是learning rate(学习率)，常设为0.1~0.001之间的常数。 $\theta^{n}$ 和 $\theta^{n-1}$ 分别代表本次迭代得到的新的参数向量和上次迭代的参数向量。最关键的是梯度( $\frac{\partial J(\theta^{n-1})}{\partial\theta^{n-1}}$ )的含义。不严格的说，我们可以把梯度理解为导数，例如二次函数 $f (x)$ 的最低点是我们想要到达的目的地，此刻我在最低点的左边函数曲线上，我想要往最低点走，就要向着导数的负方向走才是正确的方向，反应到数值上就是我下一次更新的参数应该增大，而不是减小。那么增大多少呢？显然是 $\alpha$ 乘以导数，这么大。你理解了吗？
在这里插入图片描述
最后需要注意的地方是，在最开始，机器显然并不知道正确的参数( $\theta_0,\theta_1$ )是多少，因此第一次我们可以随机初始化一个 $\theta_0$ 和 $\theta_1$ ，之后就按照梯度下降对参数进行更新即可。

def gradient_descent(arg,lr,grad):
    return arg - lr * grad

求导过程

$\frac{\partial J(\theta^{n-1})}{\partial\theta^{n-1}}$ 具体怎么求解呢？因为机器自己不会求导，因此这部分还需要我们自己手动去推导，并转换成代码。这里我们使用链式求导法则，先对 $h$ 求偏导，在对 $\theta$ 求偏导。
$\frac{\partial J(\theta_0,\theta_1)}{\partial\theta_0} = \frac{\partial J}{\partial h}\frac{\partial h}{\partial\theta_0} = \frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})\newline \frac{\partial J(\theta_0,\theta_1)}{\partial\theta_1} =\frac{\partial J}{\partial h}\frac{\partial h}{\partial\theta_1} =\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x^{(i)} \newline$

def mse_linear_gradient(x,y,fn):
    m = len(x)
    y_hat = fn(x) 
    a_grad,b_grad = (1/m) * np.sum((y_hat-y)*x) , (1/m) * np.sum((y_hat-y))
    return (a_grad,b_grad)

模型编写

有了上面的思路和基础，就万事俱备，只欠东风了。我们只需要把梯度下降迭代的过程用代码表达出来就可以了。为了使得接口更通用，可以设置两个超参数max_iter和lr，分别表示最大迭代次数和学习率。

class linear_model:
    def __init__(self,max_iter=100,lr=0.01):
        self.max_iter = max_iter
        self.lr = lr
    def fit(self,data):
        x,y = data
        # 初始再一定范围内随机 a,b
        a,b = [random.randint(-1,1) for i in range(2)]
        f = gf(a,b)
        # 使用梯度下降优化 + MSE_Loss 迭代求解线性模型的参数
        for i in range(self.max_iter):
            # 计算Loss
            loss = MSE_Loss(x,y,f)
            print("loss",loss)
            # 计算梯度
            a_grad,b_grad = gradient(x,y,f)
            # 梯度下降，更新参数
            a = gradient_descent(a,self.lr,a_grad)
            b = gradient_descent(b,self.lr,b_grad)
            print(a,b)
            # 更新模型
            f = gf(a,b)
        return f

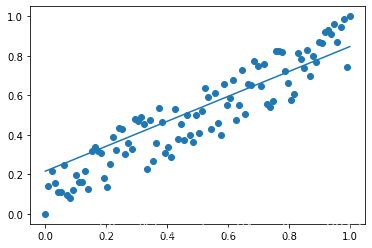
模型训练与验证

可以看到，经过300次的迭代，最终得到了一条还算不错的函数，大致反应了数据点的分布趋势情况。细心的读者可能会发现这张图中 $x, y$ 的数值范围被放缩到了 $[0, 1]$ 之间，对应的操作就是minmax_normalize，这就是机器学习中常用到的归一化操作。这步操作的目的有很多，例如，归一化可以使得梯度朝着最优解方向，进而加快寻优速度；归一化还可以将不同量纲的数据放缩到同一量纲内，使得各个特征权重分布合理；归一化还有一个优点，就是防止梯度爆炸和梯度消失，这也是这个例子中不得不进行归一化的原因，我将在下一节详细阐述这个事情。到目前为止，我们用一个线性回归的简单例子，讲述了机器学习的通用的框架步骤，不知道你明白了吗？

# Normalization
def minmax_normalize(x):
    return (x-np.min(x))/(np.max(x)-np.min(x))
model = linear_model(max_iter=300)
# 数据归一化 MinMax
x,y = minmax_normalize(x),minmax_normalize(y)
f = model.fit((x,y))
plt.scatter(x,y)
plt.plot(x,f(x))
plt.show()

在这里插入图片描述

未归一化导致的梯度爆炸

如果你尝试将这个例子中归一化操作去掉，并把max_iter改为100，就像这样。

model = linear_model(max_iter=100)
f = model.fit((x,y))
plt.scatter(x,y)
plt.plot(x,f(x))
plt.show()

那我们会得到一个匪夷所思的结果。
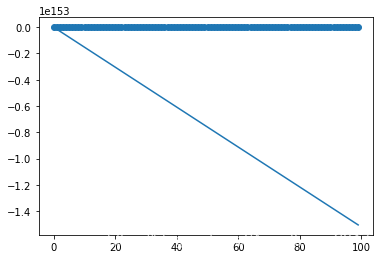
在这里插入图片描述
查看中间的loss输出以及 $a, b$ 的更新，我们会发现loss不减反增，甚至增大到了 $3.7 e + 302$ 这样的数量级， $a, b$ 也是同样情况。如果我们继续增大max_iter到300，我们会发现loss的输出中多了很多inf和nan。inf是python中的无穷大的表示方法，也即梯度增大到了无穷大。nan表示 Not A Number，产生nan的情况有很多，比如 $i n f / i n f, i n f ? i n f$ 等都会产生nan值。因此综合来看，我们的模型发生了梯度爆炸，也即梯度在计算的过程中大的离谱。

我们来看看，梯度爆炸是如何产生的。下面是未经归一化的数据在训练过程中的一组值， $y\_h$ 表示模型当前预测值， $y$ 表示原始数据中的值，经过一次梯度的计算，我们发现梯度的数量级已经到了千万量级。这样大的梯度会导致参数的更新也发生极大的改变，进一步导致 $y\_h$ 中的值范围变得更大，这样下一次计算梯度会更大，依次恶行迭代，导致Loss的值越来越大，梯度也越来越大，最终大到无穷大或无穷小，无法继续计算，便会得到nan值。

y_h = np.array([-76,-166,-256,-346,-436,-526,-616,-706,-796,-886,-976 ,-1066
 ,-1156 ,-1246 ,-1336 ,-1426 ,-1516 ,-1606 ,-1696 ,-1786 ,-1876 ,-1966 ,-2056 ,-2146
 ,-2236 ,-2326 ,-2416 ,-2506 ,-2596 ,-2686 ,-2776 ,-2866 ,-2956 ,-3046 ,-3136 ,-3226
 ,-3316 ,-3406 ,-3496 ,-3586 ,-3676 ,-3766 ,-3856 ,-3946 ,-4036 ,-4126 ,-4216 ,-4306
 ,-4396 ,-4486 ,-4576 ,-4666 ,-4756 ,-4846 ,-4936 ,-5026 ,-5116 ,-5206 ,-5296 ,-5386
 ,-5476 ,-5566 ,-5656 ,-5746 ,-5836 ,-5926 ,-6016 ,-6106 ,-6196 ,-6286 ,-6376 ,-6466
 ,-6556 ,-6646 ,-6736 ,-6826 ,-6916 ,-7006 ,-7096 ,-7186 ,-7276 ,-7366 ,-7456 ,-7546
 ,-7636 ,-7726 ,-7816 ,-7906 ,-7996 ,-8086 ,-8176 ,-8266 ,-8356 ,-8446 ,-8536 ,-8626
 ,-8716 ,-8806 ,-8896 ,-8986])
y = np.array([145 ,129 ,78 ,107 ,48 ,178 ,55 ,151 ,229 ,169 ,145 ,81 ,231 ,210 ,128 ,88 ,242 ,259
 ,95 ,217 ,188 ,280 ,131 ,157 ,182 ,302 ,174 ,262 ,251 ,210 ,342 ,248 ,246 ,337 ,318 ,261
 ,335 ,360 ,212 ,244 ,316 ,263 ,229 ,378 ,324 ,344 ,417 ,306 ,353 ,378 ,346 ,257 ,354 ,393
 ,321 ,431 ,382 ,436 ,458 ,295 ,426 ,479 ,462 ,458 ,484 ,497 ,495 ,489 ,437 ,484 ,484 ,537
 ,469 ,389 ,438 ,393 ,471 ,432 ,550 ,504 ,582 ,496 ,555 ,539 ,607 ,523 ,431 ,632 ,548 ,537
 ,585 ,586 ,584 ,624 ,610 ,477 ,534 ,587 ,527 ,501])
np.sum((y_h-y)*x)
# output : -32103025