[人工智能]神经网络数学模型快速入门-数学建模之matlab实现

多层前向神经网络原理介绍

多层前向神经网络原理介绍
多层前向神经网络(MLP)是神经网络中的一种， 它由一些最基本的神经元即节点组成， 如图1。除输入层外， 每一节点的输入为前一层所有节点输出值的和。 每一节点的激励输出值由节点输入、 激励函数及偏置量决定。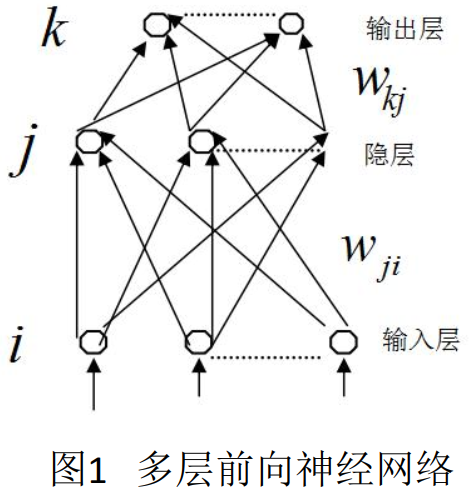

第i层为各节点的输入， 通常需要归一化到-1和1之间

在第$j$层，节点的输入值为：

? $ne{t}_j=\sum w_{ji}{o}_i+{\theta }_j$?

其中${\theta }_j$?为阈值，正阈值的作用将激励函数沿$x$??轴向左平移
节点的输出值为：

? $o_j=f\left(ne{t}_j\right)$??
式中$f$?为节点的激励函数,通常选择如下 $Sigmoid$??函数:

? $f(x)=\frac{1}{1+\exp (?x)}$?

在第k层的网络节点输入为： $ne{t}_k=\sum w_{kj}{o}_j+{\theta }_k$?

而输出为：$o_k=f\left(ne{t}_k\right)$?

对每一个输入的模式样本$p$?,平方误差$E_p$???,为：

$E_p=\frac{1}{2}{\sum }_k{\left(t_{pk}?o_{pk}\right)}^2$?

全部学习样本总误差为:

$E=\frac{1}{2p}{\sum }_p{\sum }_k{\left(t_{pk}?o_{pk}\right)}^2$?

在学习过程中,系统将调整连接权和阀值,使$E_p$尽可能快地下降。

Matlab相关函数介绍

网络初始化函数

net= newff([$x_m$,$x_M$]，[$h_1{h}_2,\dots ,h_k$]，{$f_1,f_2,\dots ,f_k$})

$x_m$?和$x_M$???分别为列向量,存储各样本数据的最小值和最大值;

第2个输入变量是一个行向量,输入各层节点数;

第3个输入变量是字符串,代表该层的传输函数.

常用 $\tan \mathrm{sig}(\mathrm{x})=\frac{1?e^{?2x}}{1+e^{?2x}},\log \mathrm{sig}(\mathrm{x})=\frac{1}{1+e^{?x}}$?

还可以用设定参数

设定迭代次数

Net.train.Param.epochs=1000

设定带动量的梯度下降算法（让学习的速度更快）

Net.train.Fcn=‘traingm’

网络训练函数

[net,tr,Y1,E1]=train(net,X,Y)

其中X为n×M矩阵，n为输入变量的个数,M为样本数
Y为m×M矩阵，m为输出变量的个数。
net为返回后的神经网络对象，tr为训练跟踪数据,tr.perf为各步目标函数值。
Y1为网络的最后输出，E1为训练误差向量

网络泛化函数

Y2=sim(net,X1)
其中X1为输入数据矩阵， 各列为样本数据。
Y2为对应输出值

神经网络实验

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EI3tiug8-1629300413263)(image-20210818175035765.png)]

Matlab程序：

x=0:0.5:10;
y=0.2*exp(-0.2*x)+0.5*exp(-0.15*x).*sin(1.25*x);
plot(x,y) %画原始数据图
net=newff([0,10],[6,1],{'tansig','tansig'});%隐层节点选6个，y是一维为1，输入输出函数都是tansig
net=train(net,x,y); %进行网络训练
x1=0:0.1:10;
y1=sim(net,x1); %数据泛化
plot(x,y,'*',x1,y1,'r'); %作对比图

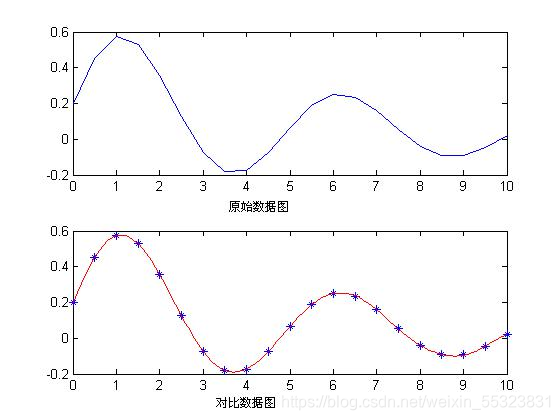
二图合一

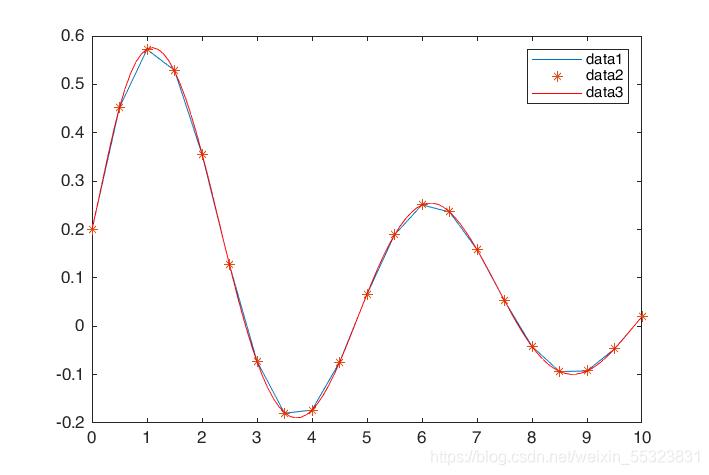
由图像可知神经网络的函数拟合能力非常强

例2 蠓的分类(MCM89A)

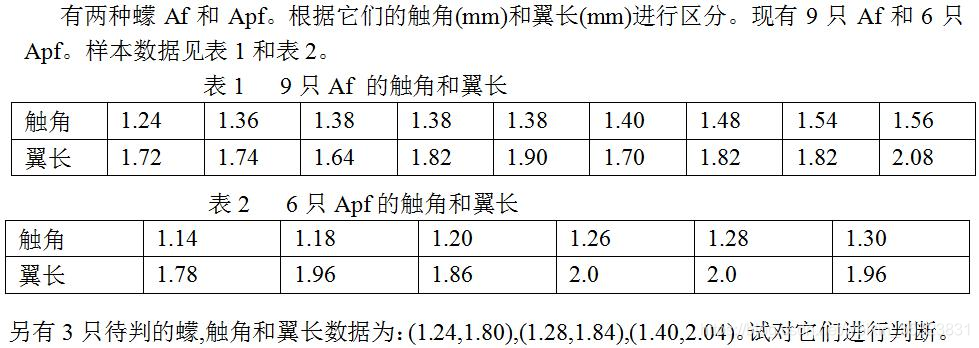
这里我们可用三层神经网络进行判别。输入为15个二维向量， 输出也为15个二维向量。
其中Af对应的目标向量为(1,0)， Apf对应的目标向量为(0,1)。

Matlab程序：

隐藏节点为5个，也可以尝试选择4，6个。网络越复杂可以选择更多，用tansig试试也可以

x=[1.24,1.36,1.38,1.38,1.38,1.40,1.48,1.54,1.56,1.14,1.18,1.20,1.26,1.28,1.30;
1.72,1.74,1.64,1.82,1.90,1.70,1.82,1.82,2.08,1.78,1.96,1.86,2.0, 2.0,1.96];
y=[1,1,1,1,1,1,1,1,1,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0,1,1,1,1,1,1];
xmin=min(x'); %求各指标最小值 %先转置，因为matlab只能对列求最大，最小，和平均值
xmax=max(x'); %求各指标最大值
net.trainParam.epochs=2500; %设定迭代步数
net=newff([xmin',xmax'],[5,2],{'logsig','logsig'}); %初始化网络 
net=train(net,x,y); %进行网络训练
x1=[1.24,1.28,1.40;
1.80,1.84,2.04];%待分样本
y1=sim(net,x1); %数据泛化
plot(x(1,1:9),x(2,1:9),'*',x(1,10:15),x(2,10:15),'o',x1(1,:),x1(2,:),'p') %画数据图
grid on

三个样本输出值：
y1=0.1235 0.8995 0.0037
0.8785 0.0951 0.9986

? 图3 Af， Apf及待分样本数据图

?