本次学习笔记是观看P3-P4之后写的。
本次的内容主要是对回归进行了简单地介绍。
回归就是找到一个函数,通过特征,输出数值。
回归模型步骤:
(1)模型假设,选择模型框架(线性模型)
(2)模型评估,如何判断模型的好坏(损失函数)
(3)模型优化,如何筛选最优的模型(梯度下降)
1.模型假设 - 线性模型
线性模型分为:
(1)一元线性模型(单个特征)
(2)多元线性模型(多个特征)
线性模型为
y
=
b
+
∑
w
i
?
x
i
y= b + \sum{w_{i}*x_{i}}
y=b+∑wi??xi?
x
i
x_i
xi?是各种特征
w
i
w_i
wi?是各个特征的权重
b
b
b是偏移量
2.模型评估 - 损失函数
是使用模型预测的值和真实的值的差来判断一个模型的好坏。
对于10个数据的为损失函数 Loss function:
L
(
w
,
b
)
=
∑
n
=
1
10
(
y
^
n
?
f
(
x
c
p
n
)
)
2
=
∑
n
=
1
10
(
y
^
n
?
(
b
+
∑
w
i
?
x
i
)
)
2
L(w,b)=\sum_{n=1} ^{10}(\hat{y}^n-f(x_{cp}^n))^2 =\sum_{n=1} ^{10}(\hat{y}^n-(b + \sum{w_{i}*x_{i}}))^2
L(w,b)=∑n=110?(y^?n?f(xcpn?))2=∑n=110?(y^?n?(b+∑wi??xi?))2
3.最佳模型 - 梯度下降
我们需要找到损失函数最小的一个模型。
使用
?
L
=
{
?
L
?
w
?
L
?
b
}
g
r
a
d
i
e
n
t
\nabla{L}=\begin{Bmatrix} \frac{\partial{L}}{\partial{w}}\\ \frac{\partial{L}}{\partial{b}} \end{Bmatrix}_{gradient}
?L={?w?L??b?L??}gradient?
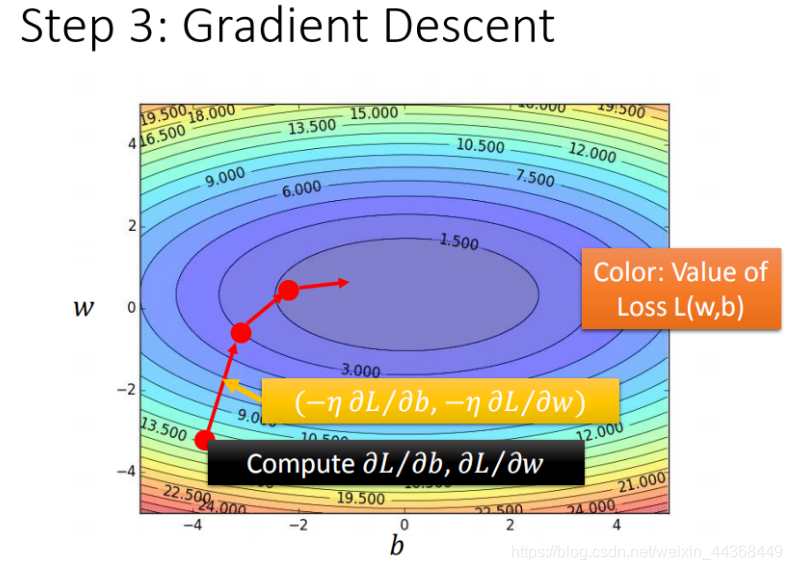
其中
η
\eta
η为学习率
验证训练好的模型的好坏是利用训练集和测试集的平均误差,取较为合适的。
不止使用1次线性模型还可以使用N次线性模型。但是不一定次数越高越好,会出现模型对训练集的过拟合这个问题。
步骤优化
(1)将输入的数据分类,每类各自建立一个模型,再通过判断将各类的模型整合到一个模型当中。
(2)寻找更多的特征和数据。
(3)加入正则化

总结

Pokemon:原始的CP值极大程度的决定了进化后的CP值,但可能还有其他的一些因素。
Gradient descent:梯度下降的做法;后面会讲到它的理论依据和要点。
Overfitting和Regularization:过拟合和正则化,主要介绍了表象;后面会讲到更多这方面的理论