[人工智能]Pytorch实验2：手动实现前馈神经网络、Dropout、正则化、K折交叉验证，解决多分类、二分类、回归任务

作者：北京交通大学计算机学院 秦梓鑫
学号：21120390
代码仅供参考，欢迎交流；请勿用于任何形式的课程作业。

一、实验内容

手动实现前馈神经网络完成回归、二分类、多分类任务

本实验的目的是使用前馈神经网络完成分类和回归问题，首先介绍前馈神经网络。对于给定的向量$x=\left[x_1,x_2,\dots ,x_n\right]$作为输入，前馈神经网络通过不断迭代以下公式进行信息传播：
$$z^{\left(l\right)}=W^{\left(l\right)}{a}^{\left(l?1\right)}+b^{\left(l\right)}$$
$$a^{\left(l\right)}=f_l\left(z^{\left(l\right)}\right)$$

其中，$a^{\left(l?1\right)}$为上一层神经元的输出，且$a^{\left(0\right)}=x$；$W^{\left(l\right)}$为第l-1层到第l层的权重矩阵；$b^{\left(l\right)}$为第l-1层到第l层的偏置；$z^{\left(l\right)}$为第l层神经元的输出活性值。然后，活性值经过激活函数得到第l层神经网络的输出$a^{\left(l\right)}$。

若任务为回归问题，可以使用均方误差作为损失函数和评价指标。一般地，若任务为分类问题，则使用Softmax回归计算每一类的概率估计，用交叉熵作为损失，用accuracy作为评价指标。计算出损失后，可利用不同优化器对损失函数进行优化求解。

利用torch.nn实现前馈神经网络完成回归、二分类、多分类任务

本部分实验目的是利用Torch.nn库中自带的函数，简洁、高效、模块化地实现实验1.1中的三个任务。

激活函数对比实验

激活函数为非线性的复合函数添加了线性的成分，是神经网络逼近函数分布的必要组成。一般地，激活函数需要满足：（1）连续且在多数点上可导；（2）是非线性函数；（3）函数和其导数需要尽可能简单，以加快计算效率；（4）函数和其导数需要落在合适的区间内。

我们选取了五种激活函数进行实验，他们分别是：

• Sigmoid函数：$\sigma \left(x\right)=\frac{1}{1+exp\left(?x\right)}\in \left(0,1\right)$
• ReLU函数：$ReLU\left(x\right)=max[0,x]$
• Tanh函数：$tanh\left(x\right)=\frac{exp\left(x\right)?exp\left(?x\right)}{exp\left(x\right)+exp\left(?x\right)}=2\sigma \left(2x\right)?1\in \left(?1,1\right)$
• Leaky ReLU函数：$LeakyReLU\left(x\right)=\{\begin{array}{ll}x& \text{?if?x≥0}\\ \gamma x& \text{if?x<0}\end{array}$
• Hard Swish函数：$ReLU6=min\left(6,max\left(0,x\right)\right)$; $Hswish\left(x\right)=x\frac{ReLU6\left(x+3\right)}{6}$

本部分实验目的是对比采用不同激活函数模型对结果的影响。

隐藏层层数和单元数对比实验

前馈神经网络中，第0层称为输入层，最后一层称为输出层，其他中间层称为隐藏层。隐藏层层数和单元数是重要的超参数。本部分实验的目的是探究此类超参数对实验结果的影响。

手动实现、torch.nn实现Dropout

训练深度神经网络时，可以随机丢弃一部分神经元和此部分对应的连接边以避免过拟合。一般地，对于一个神经层$\text{y}=f(W\text{x}+b)$，我们可以引入一个掩蔽函数mask，使得$\text{y}=f(\text{W}mask(\text{x})+b)$；mask函数通过概率为p的伯努利分布随机生成。

从集成学习的角度解释，每做一次丢弃，可以认为是采样得到两种新的子网络。若原网络有n个神经元，则总共可以得到$2^n$个共享参数的子网络。本实验的目的是探究dropout对模型训练过程和性能的影响。

手动实现、torch.nn实现${\text{L}}_2$正则化

使用$L_2$正则化时，损失函数中增加加权的模型参数的L_2范数，以限制模型的复杂度，从而提高模型的泛化能力。本实验探究L_2正则化对训练过程和结果的影响。

手动实现10折交叉验证评估

10折交叉验证是一种评估模型性能、调整参数的方法。一般地，我们将已有数据分成10份，每次训练时，取其中一份作为验证集，剩余九份作为测试集；共循环十次。10折交叉验证保证每一个样本都作为了训练集、测试集的一部分，能更完整地反映模型的性能。

二、 实验环境及实验数据集

本实验在笔记本电脑上开展。笔记本的处理器型号为：Intel? Core? i7-10510U CPU @ 1.80GHz 2.30 GHz；RAM大小为16GB；系统环境为Windows 64位。程序运行环境是：Anaconda Shell, Python 3.8.10。

实验包含以下三个数据集：

• 回归任务数据集：包含10000个数据项\left(\textbf{x},y\right)，其中\textbf{x}是维度为500的向量，y是一维数值，服从$y=0.028+{\sum }_{i=1}^{p}0.056x_i+\epsilon$的分布。训练集大小为7000，测试集大小为3000。
• 二分类任务数据集：包含20000个数据项\left(\textbf{x},y\right)，其中：标签为1的数据，\textbf{x}服从均值为10，方差为1的正态分布。
• 多分类任务数据集：采用MNIST手写体数据集，包含60000个训练样本和10000个测试样本。每个样本是28×28的单通道图像，对应10个数字分类中的一个类。

三、实验过程

手动实现前馈神经网络

与实验一相似，手动实现多层线性模型、交叉熵损失、随机梯度下降来定义模型。由于代码量较大，此处只展示和实验一不同的多层模型的定义部分。

1.	# 多层神经网络实验用
2.	W1 = torch.tensor(np.random.normal(1, 1, (256, dim_inputs)), dtype=torch.float)
3.	b1 = torch.zeros(256, dtype=torch.float32)
4.	W2 = torch.tensor(np.random.normal(1, 1, (32, 256)), dtype=torch.float)
5.	b2 = torch.zeros(32, dtype=torch.float32)
6.	W3 = torch.tensor(np.random.normal(1, 1, (dim_outputs, 32)), dtype=torch.float)
7.	b3 = torch.zeros(dim_outputs, dtype=torch.float32)
8.	
9.	params = [W1,b1,W2,W3,b2,b3]
10.	
11.	def net(X):
12.	    X = X.view(-1, dim_inputs)
13.	    out_1 = (torch.matmul(X, W1.t())+b1)
14.	    out_2 = (torch.matmul(out_1, W2.t())+b2)
15.	    out_3 = torch.matmul(out_2, W3.t())+ b3
16.	    return out_3

基于torch.nn实现前馈神经网络

内容和实验一内容较为相似，不同的是：此次实验中，我们对代码进行了模块化处理，通过传入神经网络层(layer)的列表来构建网络。这种构建方法可以提高代码的复用率，更符合工程开发的范式。
此小节展示的面向多分类任务的代码也将在二分类和回归任务中复用。

从目录结构我们可以看出，整个程序分为了data、model和network三个模块，分别对应数据预处理、定义模型和模型的构造三个功能。
model.py是程序的主文件。首先，我们定义适用于多分类问题的网络、参数、数据，并将其作为参数传入在network.py中实现的build_network函数中，以构建网络。

1.	# 用于多分类
2.	dim_input = 784
3.	dim_output = 10
4.	data = generate_multi_class(batch_size)
5.	
6.	# 分类任务网络
7.	loss = nn.CrossEntropyLoss()
8.	layers = collections.OrderedDict([
9.	    ('L1',nn.Linear(dim_input,192)),
10.	    ('A1',nn.ReLU()),
11.	    ('drop1',nn.Dropout(p=0.2)),
12.	    ('L2', nn.Linear(192, 96)),
13.	    ('A2', nn.ReLU()),
14.	    ('drop2', nn.Dropout(p=0.1)),
15.	    ('FC', nn.Linear(96,dim_output))
16.	])
17.	
18.	net = build_network(layers)
19.	
20.	import torch.optim as opt
21.	optimizer = opt.Adagrad(net.parameters(),lr=learning_rate,weight_decay=weight_decay)

build_network函数的实现如下：

1.	def build_network(layers):
2.	    import torch.nn as nn
3.	    net = nn.Sequential(layers)
4.	    return net

网络构建完毕后，在train函数中，完成训练、优化的工作。此处只展示核心代码：

1.	def train(net, data):
2.	    # parameter: net, *data
3.	    # return train_loss, valid_loss, train_acc, valid_acc
4.	    dataset_train, dataset_test = data
5.	    for epoch in range (1,num_epochs+1,1):
6.	        acc_sum = 0
7.	        cardinatity = 0
8.	        for feature,label in dataset_train:
9.	            prediction = net(feature.view(batch_size,-1))
10.	            l = loss(prediction.squeeze(),label.long())
11.	            l.backward()
12.	            optimizer.step()
13.	            optimizer.zero_grad()

之后，进行模型的评估、可视化、并把评估结果进行储存在csv格式的文件中。其中：evaluate()、calculate()、draw()、store_list()函数的定义均在network.py模块中，函数的实现过程与实验一较为相似，故此处略去展示。对训练代码进行重构后，训练过程更加清晰、简洁。

1.	# compute
2.	loss_train = evaluate(net,dataset_train,loss,batch_size)
3.	loss_test = evaluate(net, dataset_test,loss,batch_size)
4.	acc_train = calculate(net, dataset_train,batch_size)
5.	acc_test = calculate(net, dataset_test,batch_size)
6.	# store
7.	train_loss_list.append(loss_train)
8.	test_loss_list.append(loss_test)
9.	train_acc_list.append(acc_train)
10.	test_acc_list.append(acc_test)
11.	print("epoch",epoch,"loss_train:",loss_train,"loss_test:",loss_test,"acc_train:", acc_train, "acc_test:", acc_test)
12.	# visualize
13.	draw_acc(train_acc_list,test_acc_list)
14.	draw_loss(train_loss_list,test_loss_list)
15.	#store
16.	result_list = [train_loss_list,test_loss_list,train_acc_list,test_acc_list]
17.	for result in result_list:
18.	    store_list(result,retrieve_name(result)[0]

对比不同激活函数的实验结果

此处，我们只需要对传入build_network()函数的参数layers进行修改。

1.	layers = collections.OrderedDict([
2.	    ('L1',nn.Linear(dim_input, dim_output)),
3.	    ('A1',nn.Hardswish()), #修改此处的损失函数
4.	])

评估隐藏层层数和隐藏单元个数对实验结果的影响

相似地，我们只需要对传入的列表进行修改。需要注意的是，每一层变换的转化后维数（对应Linear的第二个参数）和下一层的变化的初始维数（对应Linear的第一个参数）需要始终保持一致。此外，dim_input和dim_output代表数据的原始维数、输出的最终维数，需要和数据、问题保持一致。例如对于十分类问题，dim_output为10；对于回归问题，dim_output为1。

1.	layers = collections.OrderedDict([
2.	    ('L1',nn.Linear(dim_input,192)),
3.	    ('A1',nn.Hardswish()),
4.	    ('L2', nn.Linear(192, 96)),
5.	    ('A2', nn.LeakyReLU()),
6.	    ('FC', nn.Linear(96,dim_output))
7.	])

手动实现和用torch.nn实现dropout

手动实现dropout的基本思想是：随机生成一个mask的0/1矩阵，对权重W作乘法，使得一部分$w_{ij}=0$；以此增加模型的鲁棒性。

1.	def dropout(X,drop_prob):
2.	    X = X.float()
3.	    assert 0<= drop_prob <=1
4.	    keep_prob = 1 - drop_prob
5.	    if keep_prob ==0:
6.	        return torch.zeros_like(X)
7.	    mask = (torch.rand(X.shape)<keep_prob).float()
8.	    return mask * X / keep_prob

需要特别注意的是，dropout只能在训练过程中开启

1.	def net(X,is_training):
2.	    X = X.view(-1, dim_inputs)
3.	    if is_training:  #训练时开启Dropout
4.	        dropout(W1,drop_prob=0.1)
5.	    out_1 = (torch.matmul(X, W1.t())+b1)
6.	    return out_1

在进行评估(evaluation)时，必须禁止(disable)之前的dropout模块，否则训练使用的只是剪枝后的局部网络。

1.	def evaluate_test_loss(data_iter,net,loss):
2.	    loss_sum = 0
3.	    count = 0
4.	    for X, y in data_iter:
5.	        yhat = net(X,False)
6.	        l = loss(yhat, y).sum() + lambd *l2_panalty(W1).sum()
7.	        loss_sum += l
8.	        count += y.shape[0]
9.	    return (loss_sum/count).item()

在torch中，使用dropout只需要在layers中额外添加一个dropout层：

1.	loss = nn.CrossEntropyLoss()
2.	layers = collections.OrderedDict([
3.	    ('L1',nn.Linear(dim_input,192)),
4.	    ('A1',nn.Hardswish()),
5.	    ('drop1', nn.Dropout(p=0.1)), # dropout layer 1
6.	    ('L2', nn.Linear(192, 96)),
7.	    ('A2', nn.LeakyReLU()),
8.	    ('drop2', nn.Dropout(p=0.1)), # dropout layer 2
9.	    ('FC', nn.Linear(96,dim_output))
10.	])

手动实现和用torch.nn实现${\text{L}}_2$正则化

手动计算参数的$L_2$范数：

1.	def l2_panalty(w):
2.	    return (w**2)/2

添加到Loss中，实现正则化：

1.	for X, y in train_iter:
2.	    yhat = net(X,True)
3.	    l = loss(yhat, y).sum() + lambd * l2_panalty(W1).sum() # must sum since l2(W1) is a matrix; loss must be scalar
4.	    for param in params:
5.	          if param.grad is not None:
6.	              param.grad.data.zero_()
7.	    l.backward()
8.	    SGD(params, lr,batch_size)

在torch中，定义正则化只需要修改优化器的weight_decay参数即可。

1.	import torch.optim as opt
2.	optimizer = opt.Adagrad(net.parameters(),lr=learning_rate,weight_decay=weight_decay)

手动实现10折交叉验证评估

实现10折交叉验证的核心部分代码如下，get_k_fold_data()函数接收特征和标签张量，生成交叉验证的特征和标签。

1.	def get_k_fold_data(k,i,X,Y,batch_num):
2.	    fold_size = Y.shape[0]// k # int operation
3.	    val_start = i * fold_size
4.	    if i != k-1:
5.	        val_end = (i+1) * fold_size # the next step
6.	        X_valid, Y_valid = X[val_start:val_end], Y[val_start:val_end]
7.	        X_train, Y_train = torch.cat((X[0:val_start],X[val_end:]),dim=0),torch.cat((Y[0:val_start],Y[val_end:]),dim=0)
8.	    else: # add all remaining elements
9.	        X_valid, Y_valid = X[val_start:], Y[val_start:]
10.	        X_train, Y_train = X[0:val_start], Y[0:val_start]

四、实验结果

多分类任务

手动实现前馈神经网络

使用单层线性模型，epochs数为10，batch大小为10，学习率为0.01时，可以观察到训练集、测试集上loss的下降。

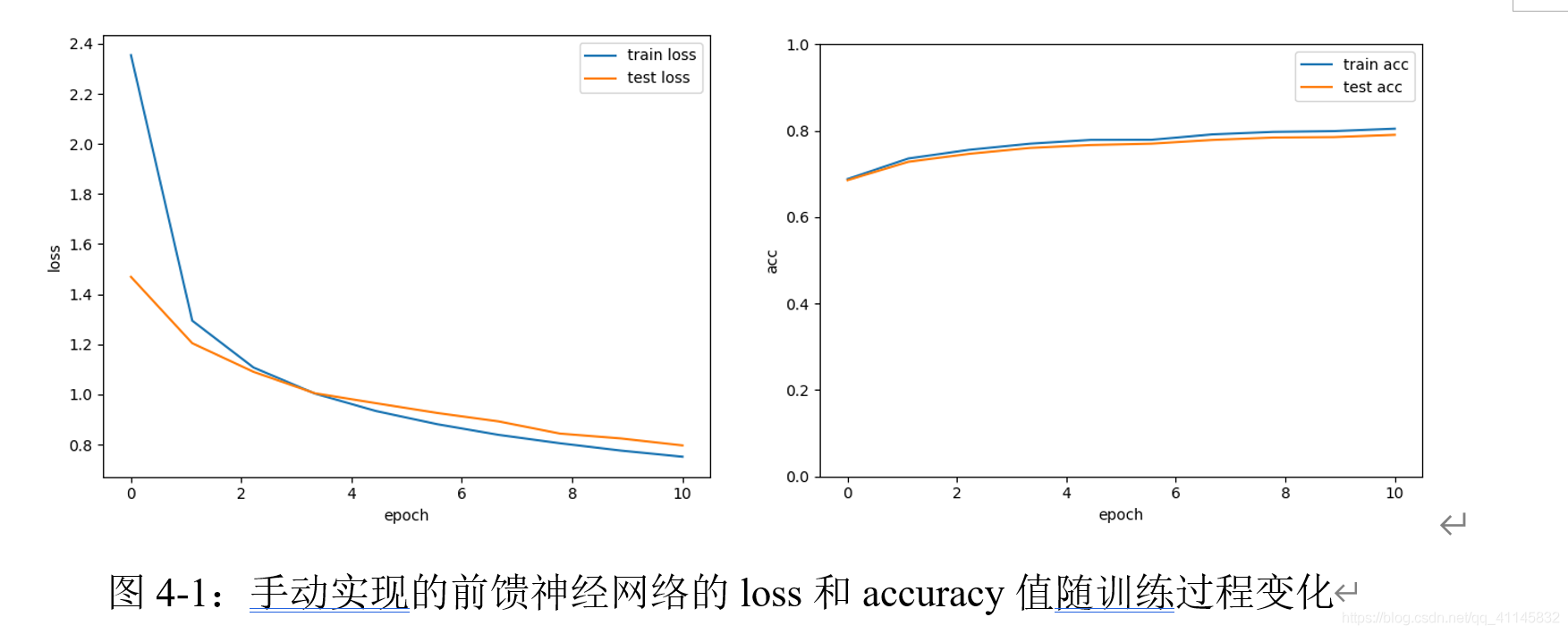
由于可能存在的数值方面原因，使用手动实现的多层线性模型进行优化时，Softmax函数的输出趋近于01二项分布，导致损失函数输出值为NaN，无法进行优化。

利用torch.nn实现前馈神经网络

使用ReLU作为激活函数的3层前馈神经网络，epochs数为10，batch大小为10，学习率为0.001时，可以观察到训练集、测试集上loss的下降。

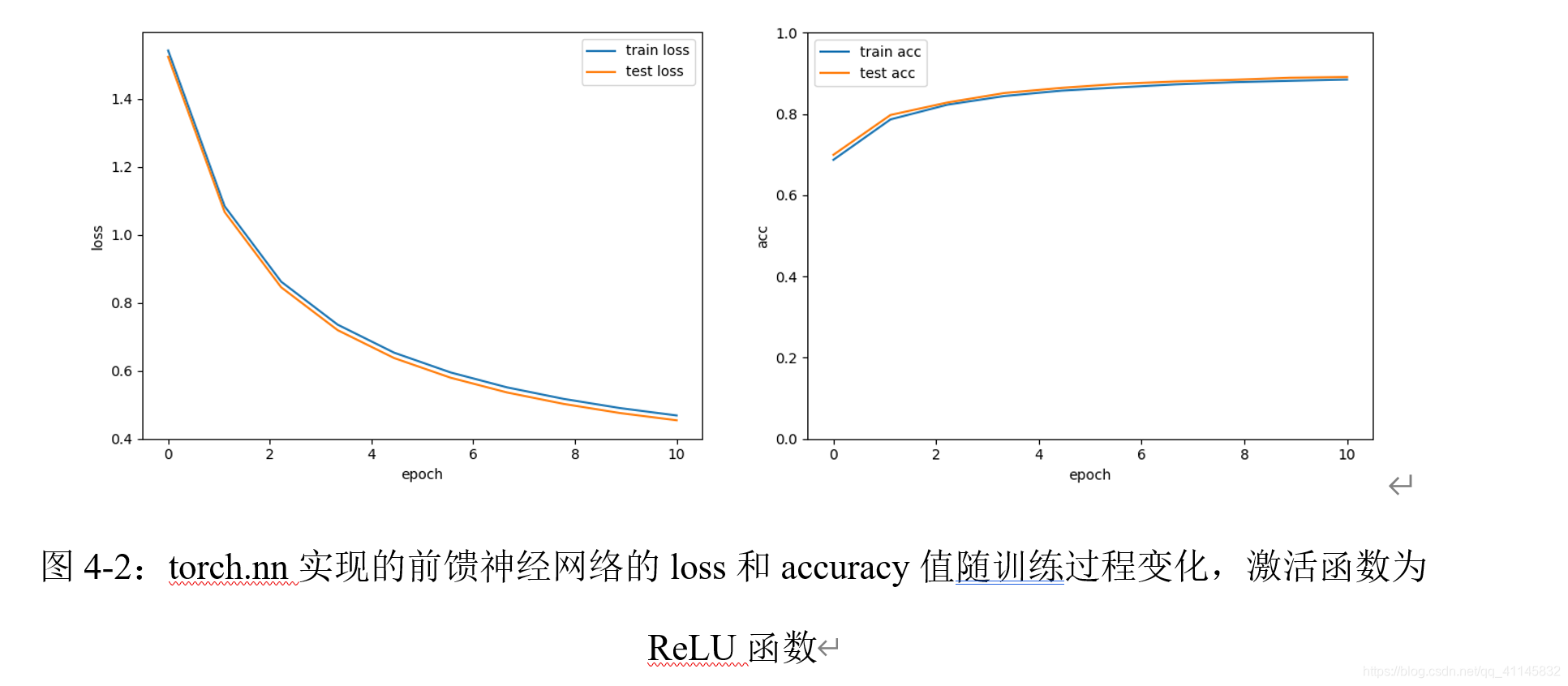
对比使用不同激活函数的实验结果

采用与实验（3）相同的架构，其它激活函数的实验结果如下。


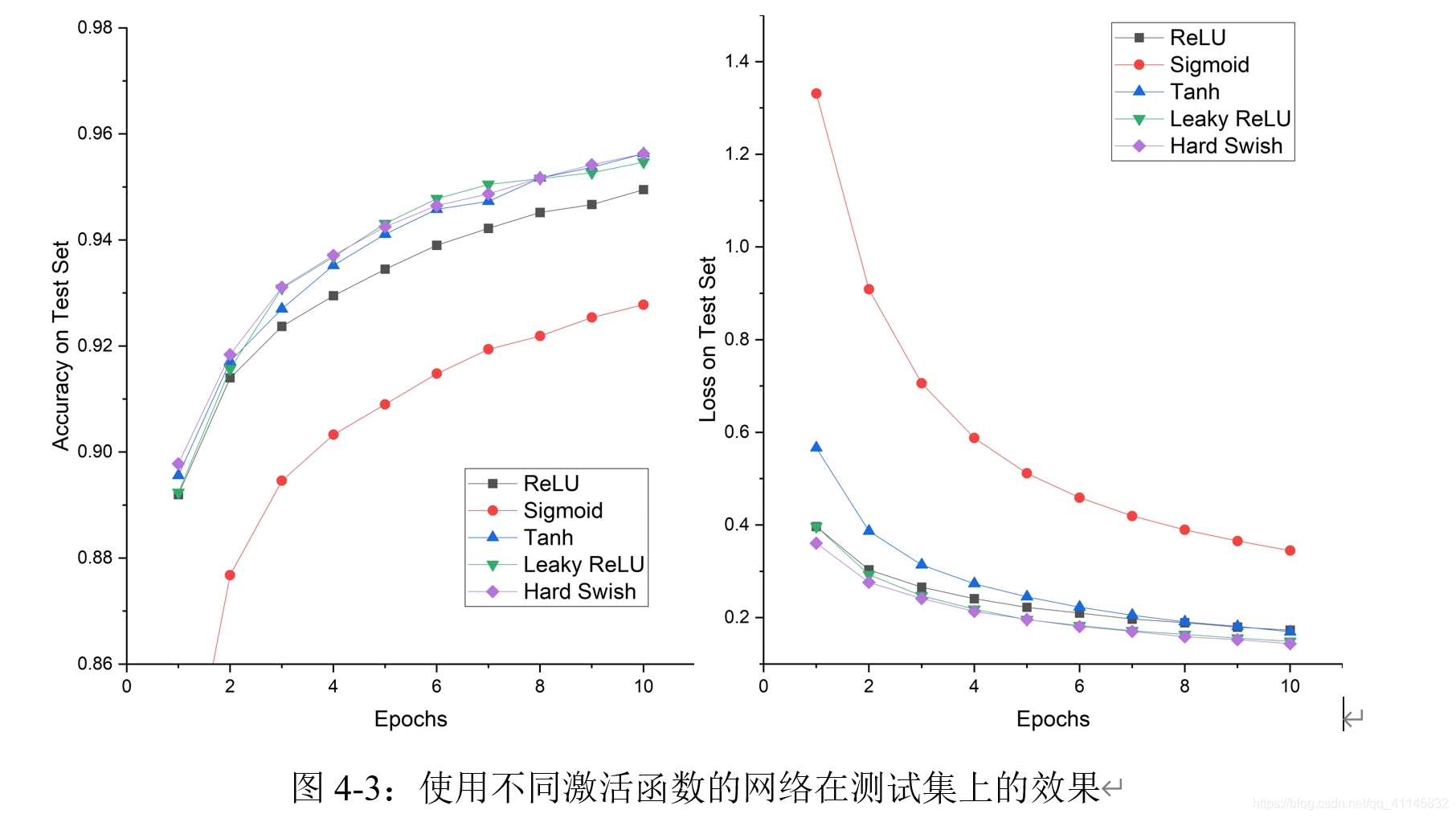
对比五种激活函数的实验结果，我们发现：

• 采用Sigmoid函数时，实验得到的最佳学习率为0.01；相比于ReLU函数使用的学习率更大一些，但效果落后于其它的激活函数。
• Tanh函数作为激活函数时，loss收敛较快，accuracy较高。
• Hard Swish函数accuracy上升速度快，后期区域趋势平稳。
• 收敛时，Hard Swish和Leaky ReLU效果相差较小，是表现最优的两个函数。

评估隐藏层层数和隐藏单元个数对实验结果的影响

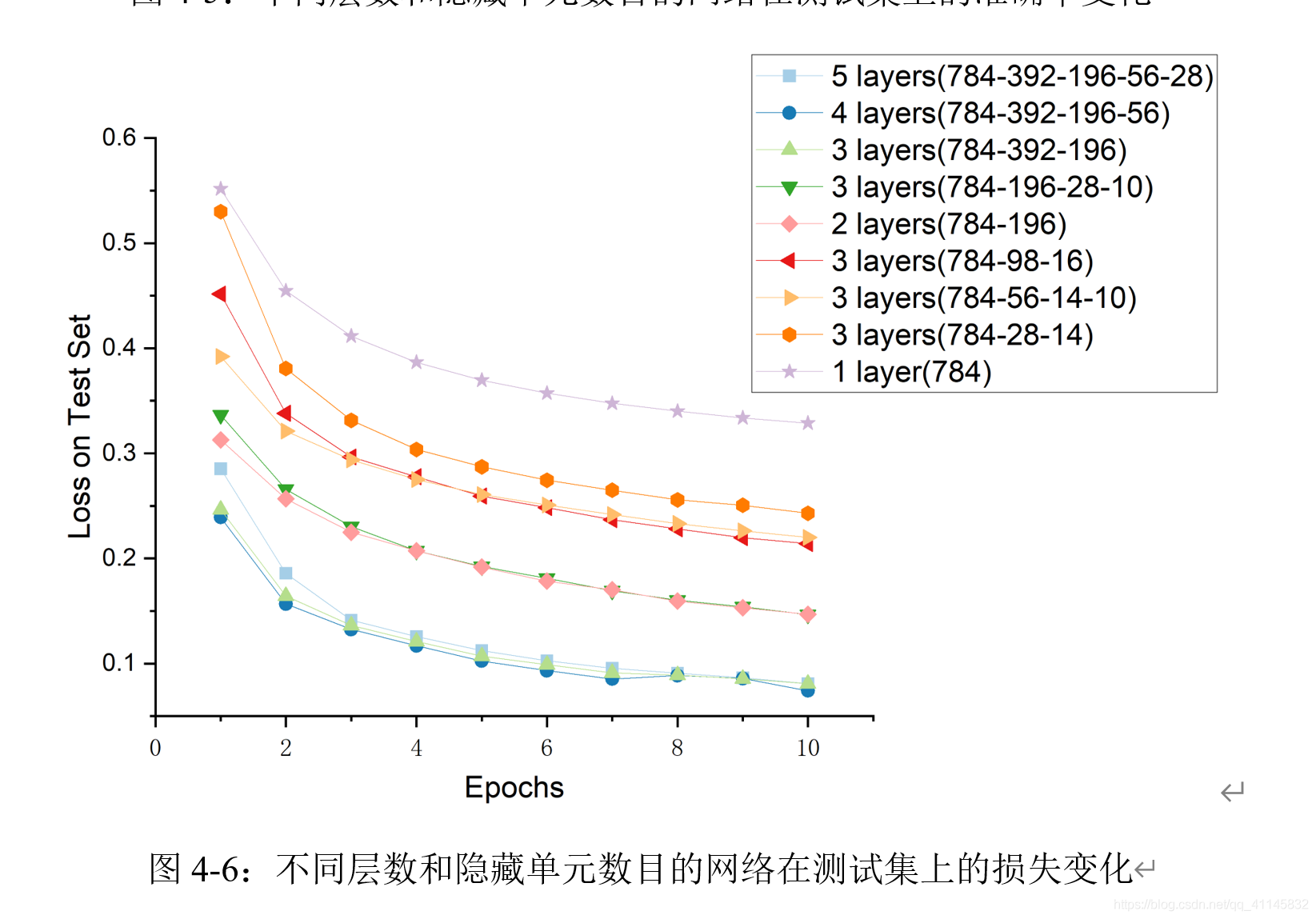
手动实现和用torch.nn实现dropout

手动实现dropout

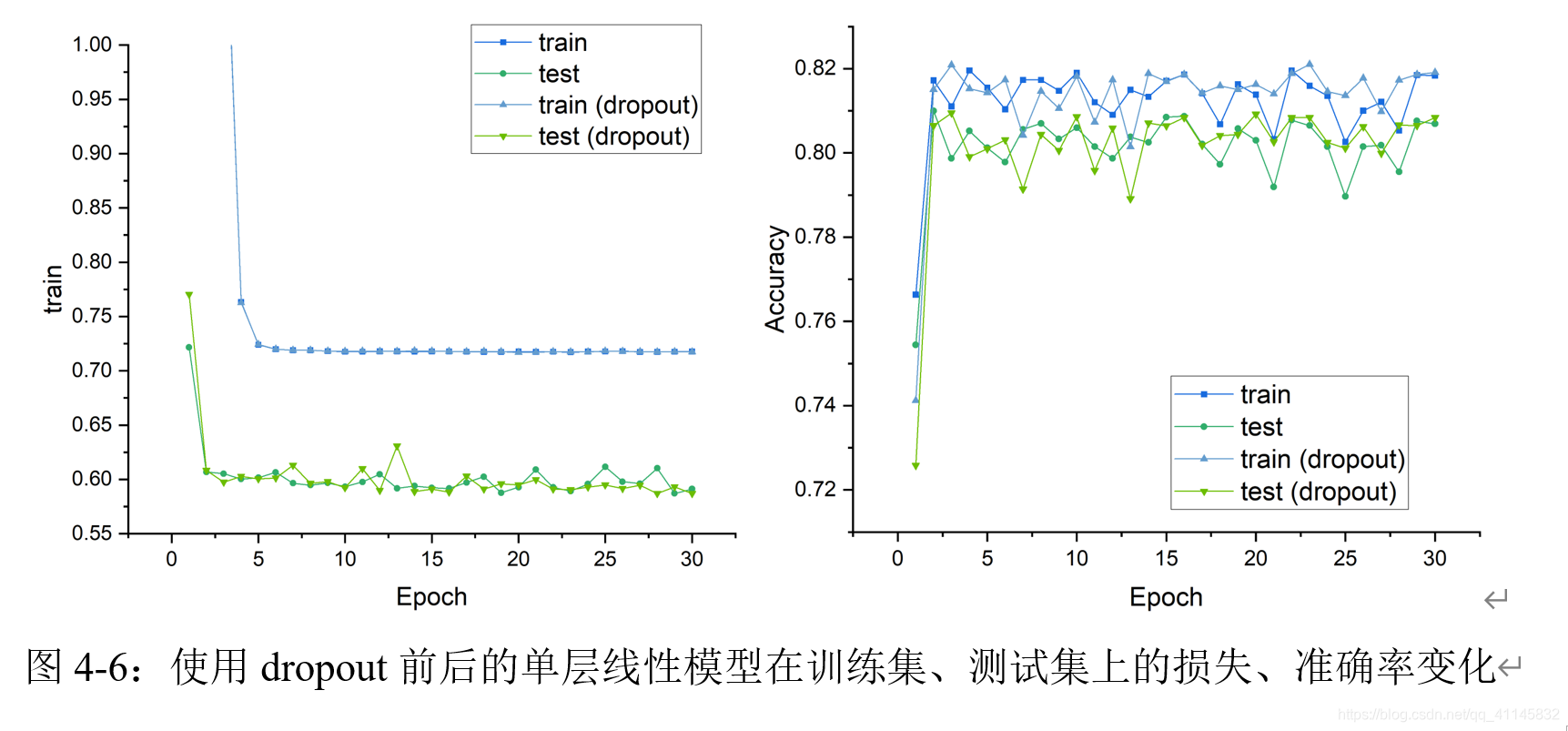由于手动实现的神经网络具有较低的数值稳定性，在dropout率p>=0.2时，会出现Loss为NaN的现象，故实验只记录了两组数据。如上图所示，浅色曲线代表使用dropout后的模型效果，可以发现：使用dropout后，在测试集上的效果随训练次数变化曲线会出现一定的波动，有助于模型避免过拟合。

利用torch.nn实现dropout

单层神经网络，使用Sigmoid作为激活函数，不使用Dropout时，表现如下：

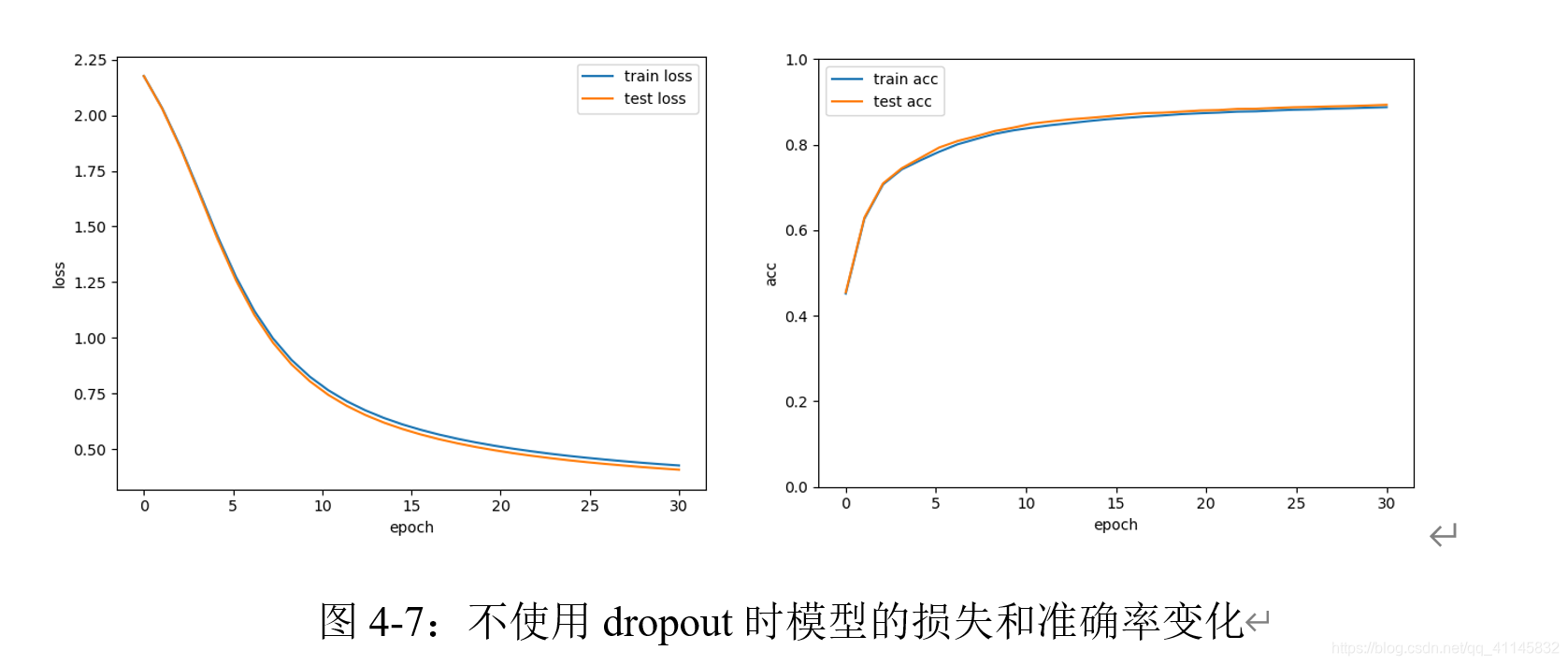
可以观察到，此时训练集和测试集的准确率变化基本一致。
添加Dropout层后，模型表现如下：


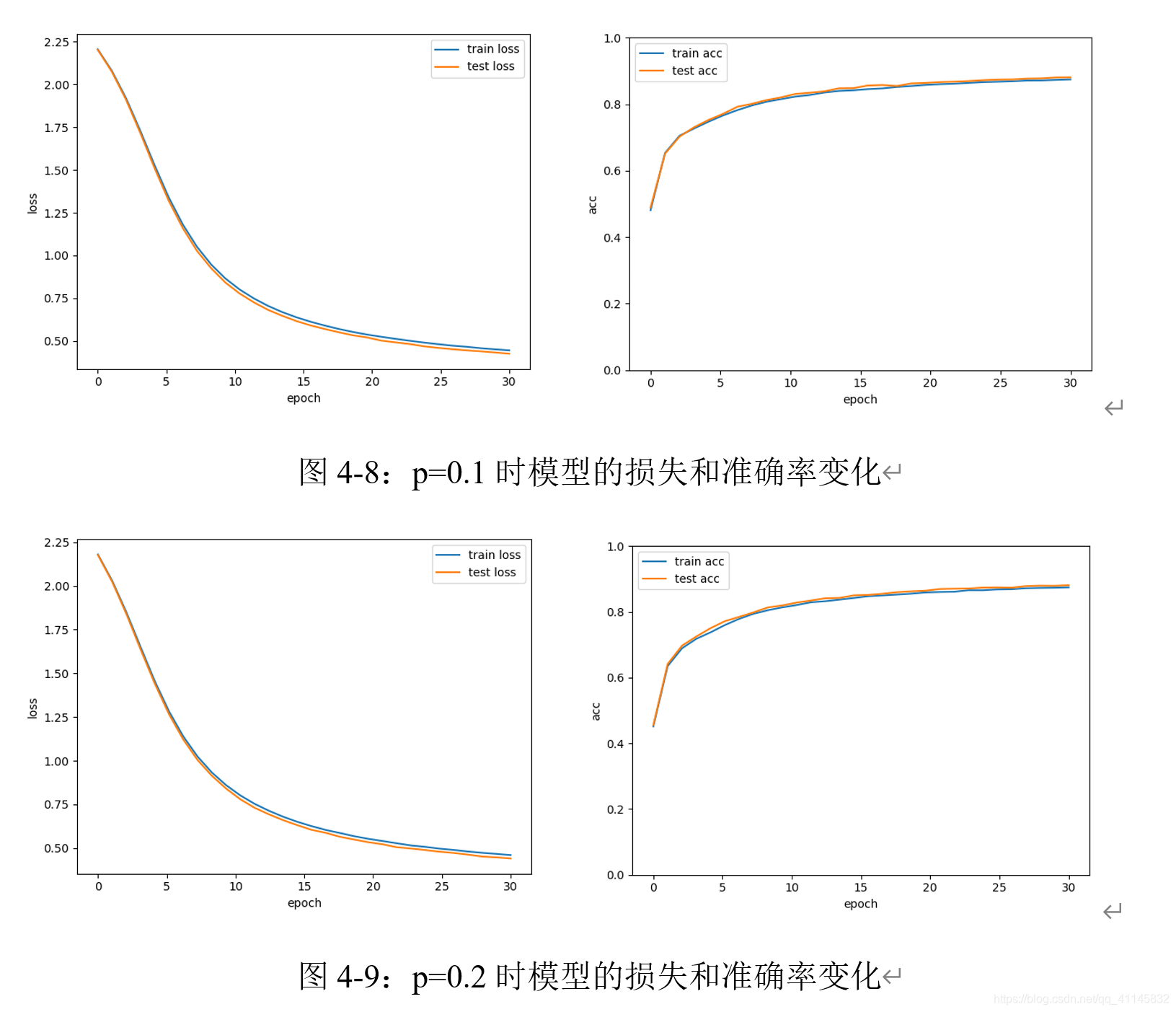
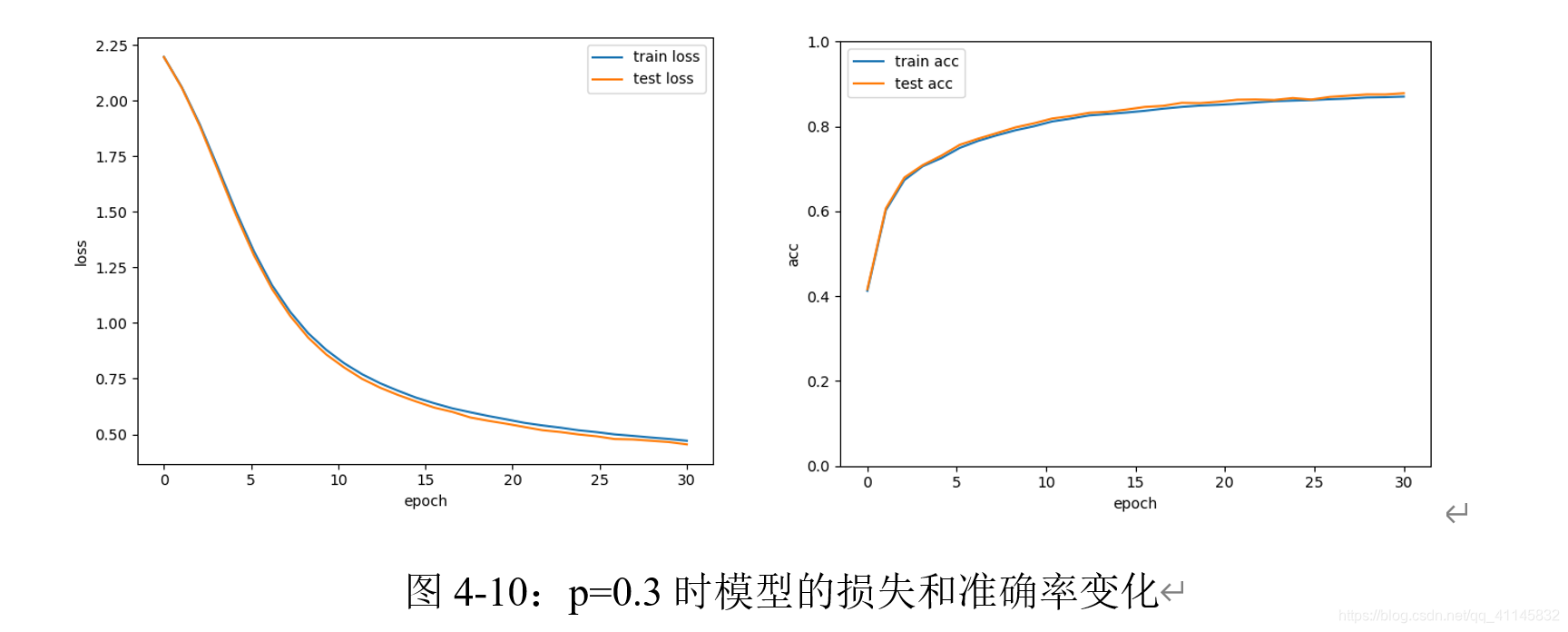
可以观察到，当dropout率增加到0.3时，测试集上的准确率明显高于训练集。使用更大的训练集、增加训练次数时，dropout的效果可能更充分。

手动实现和用torch.nn实现L_2正则化

手动实现$L_2$正则化

实验中，我们以$\lambda =0.2$为参数添加了正则化。可以观察到，添加正则化之后，模型收敛速度迅速提升，在训练集和测试集上的Loss差异大幅减小；但同时，模型的Loss后期趋于稳定，在固定的训练次数下，无法收敛到更高的精度。

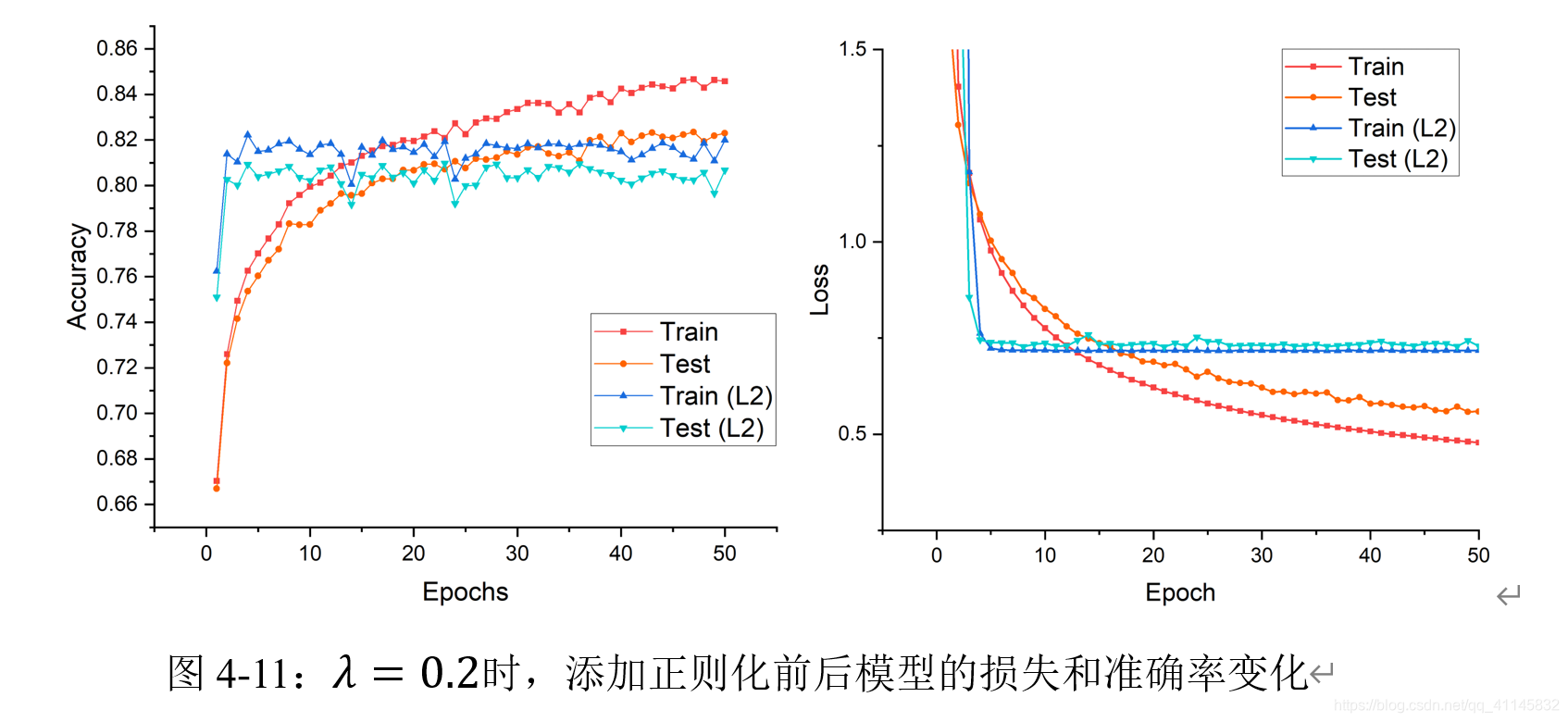
torch.nn实现$L_2$正则化

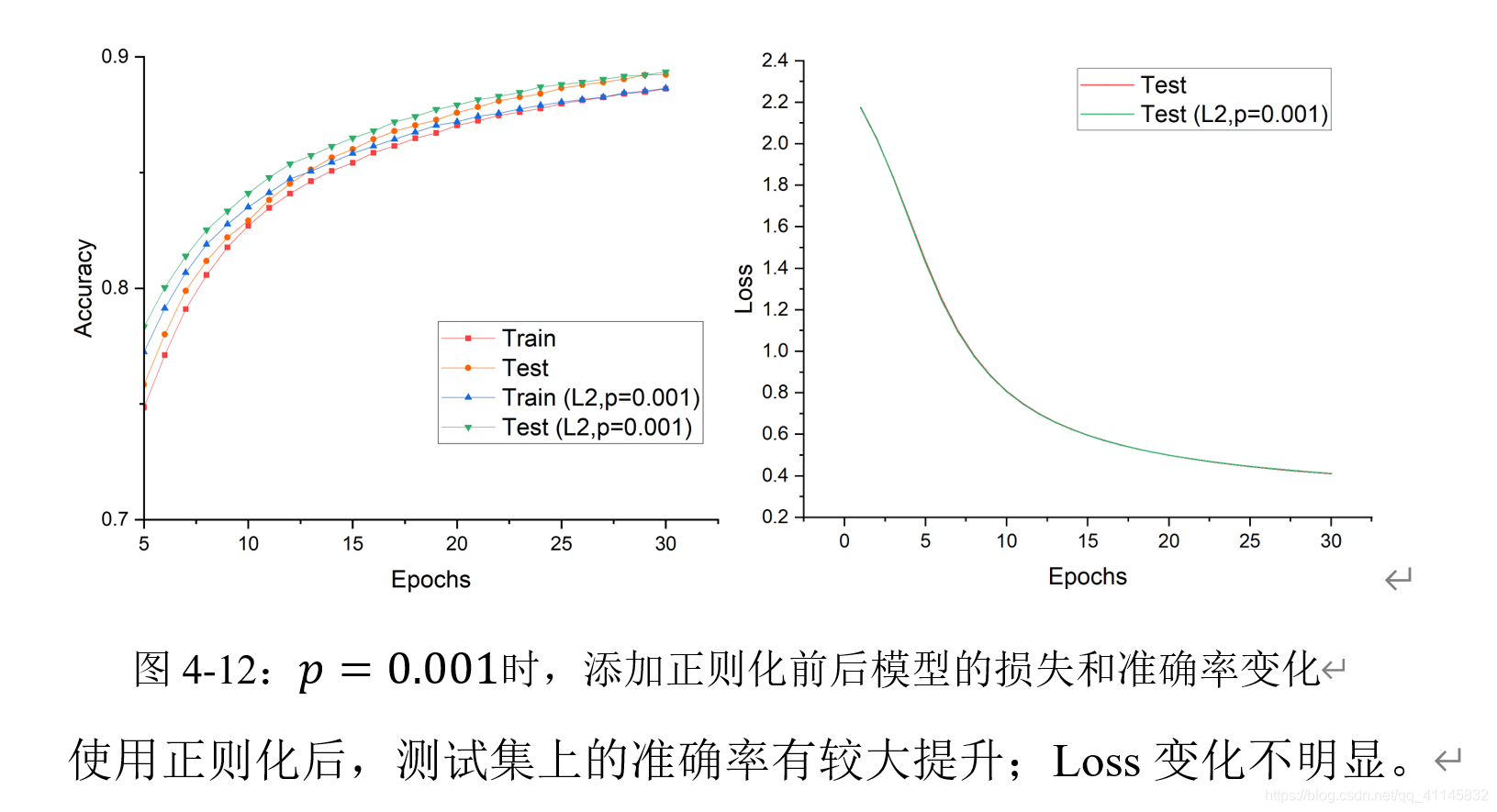
手动实现10折交叉验证评估

Epoch为10、学习率为0.01、L_2正则化比率设为0.0001、批量数为10时，对以下模型进行训练：

10折交叉验证结果如下：

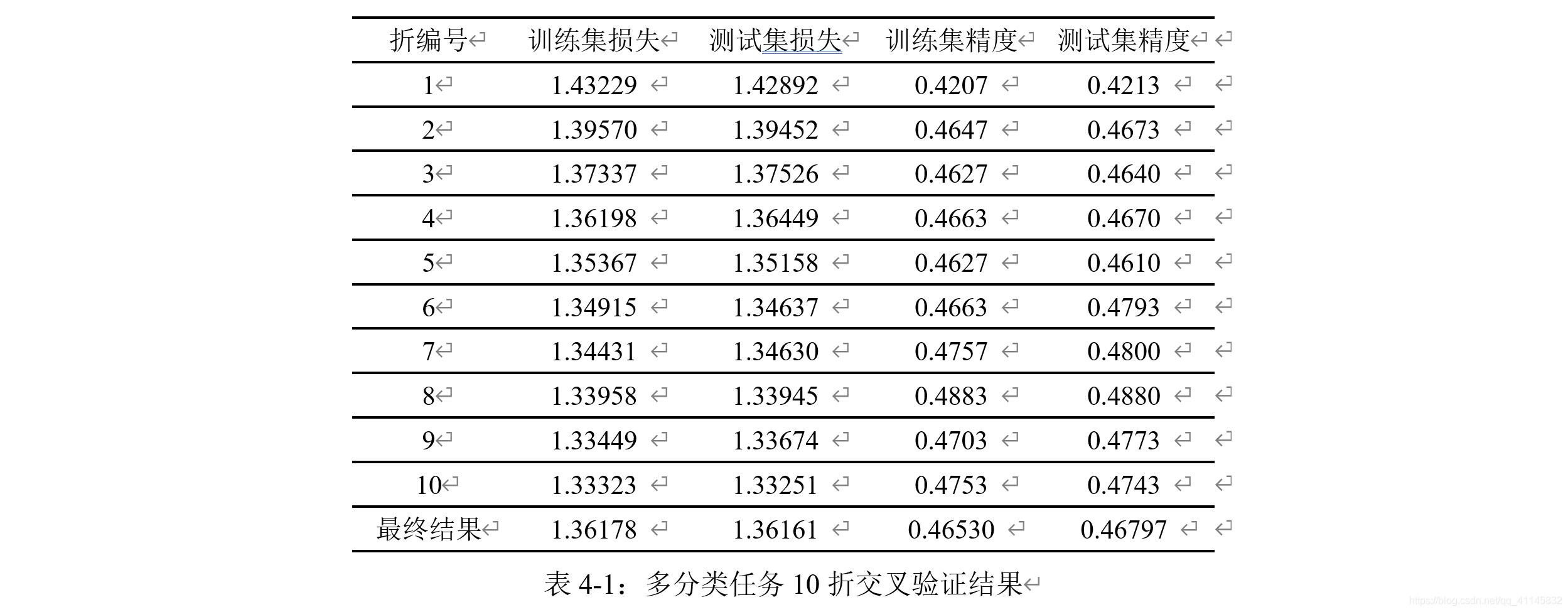
二分类任务

手动实现前馈神经网络

学习率设置为1e-5，批量数为1000，在ReLU函数激活的单层神经网络迭代20次的结果如下

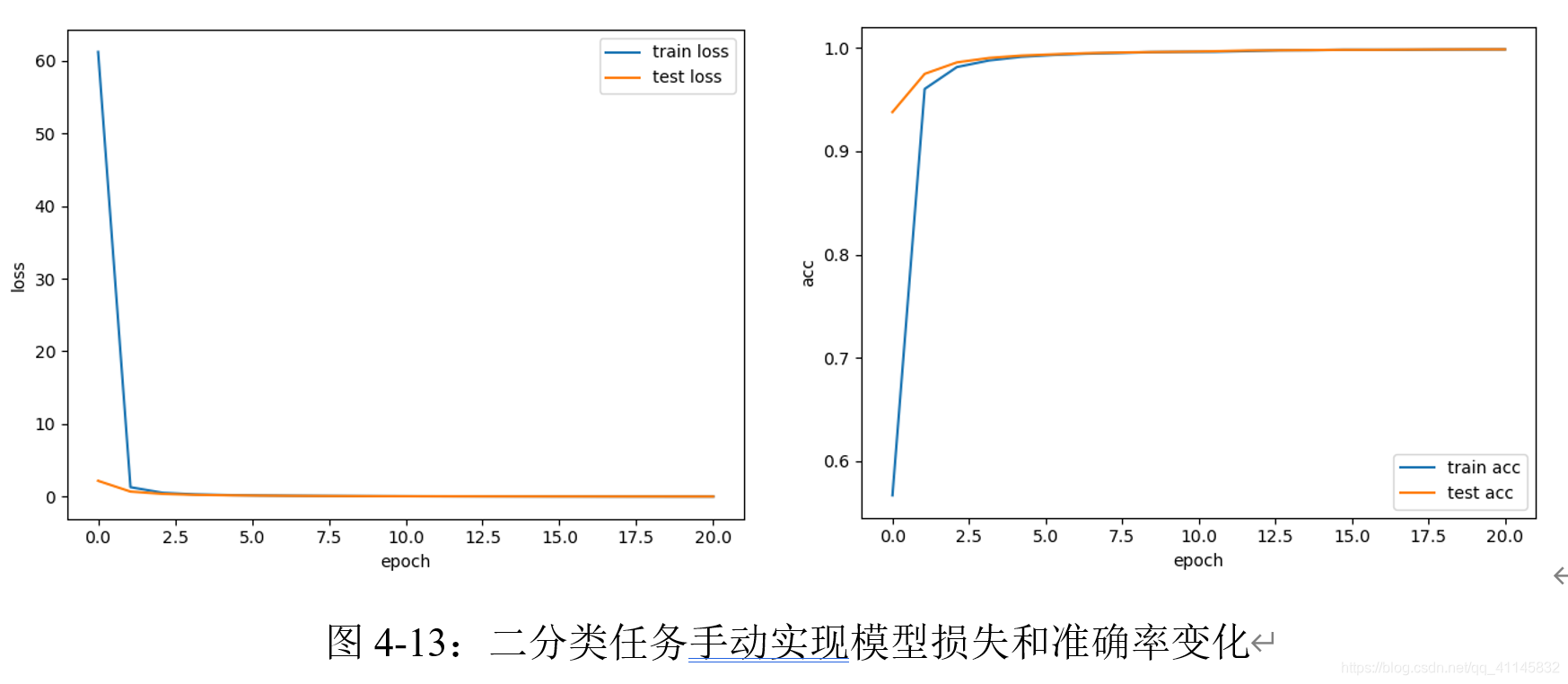
利用torch.nn实现前馈神经网络

采用相同的参数设定，迭代十次的结果如下：

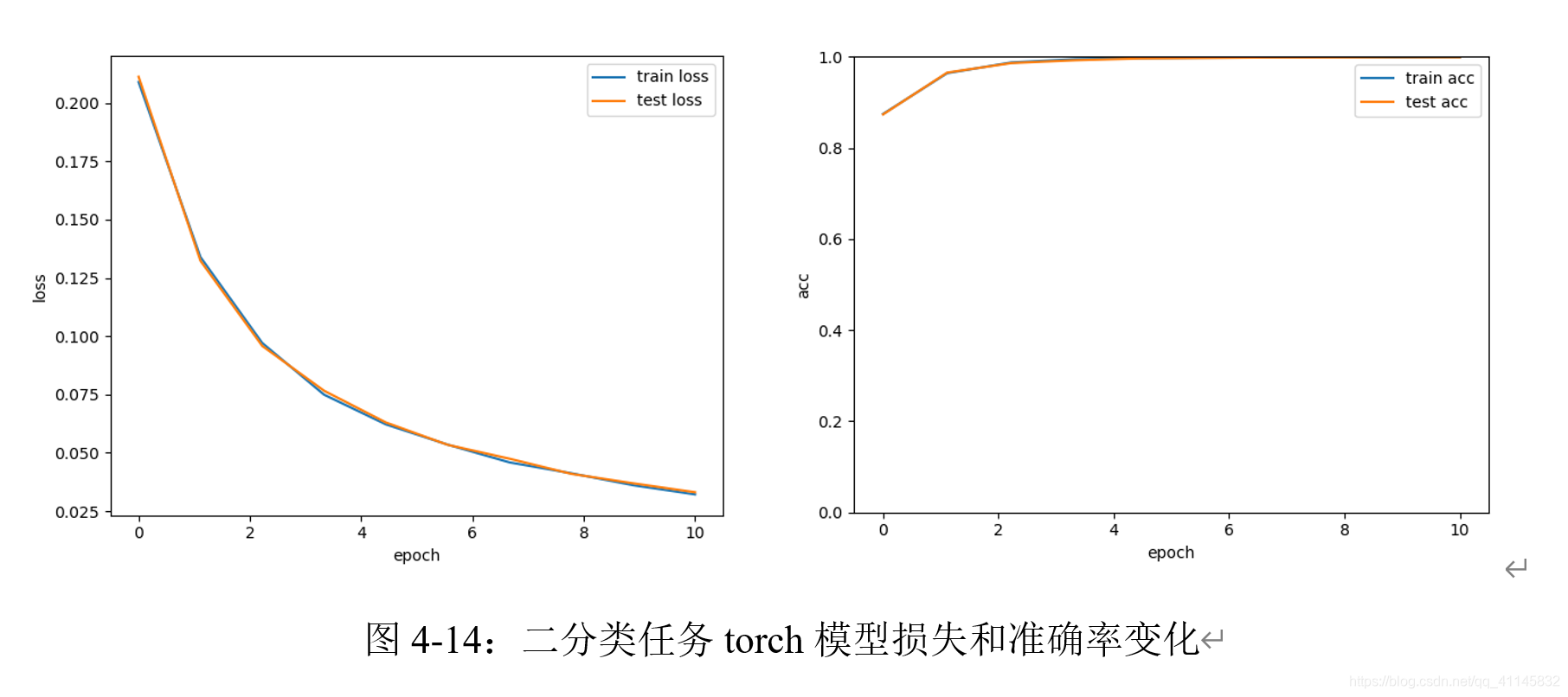
实现10折交叉验证评估

在二分类数据集上得到的结果如下：

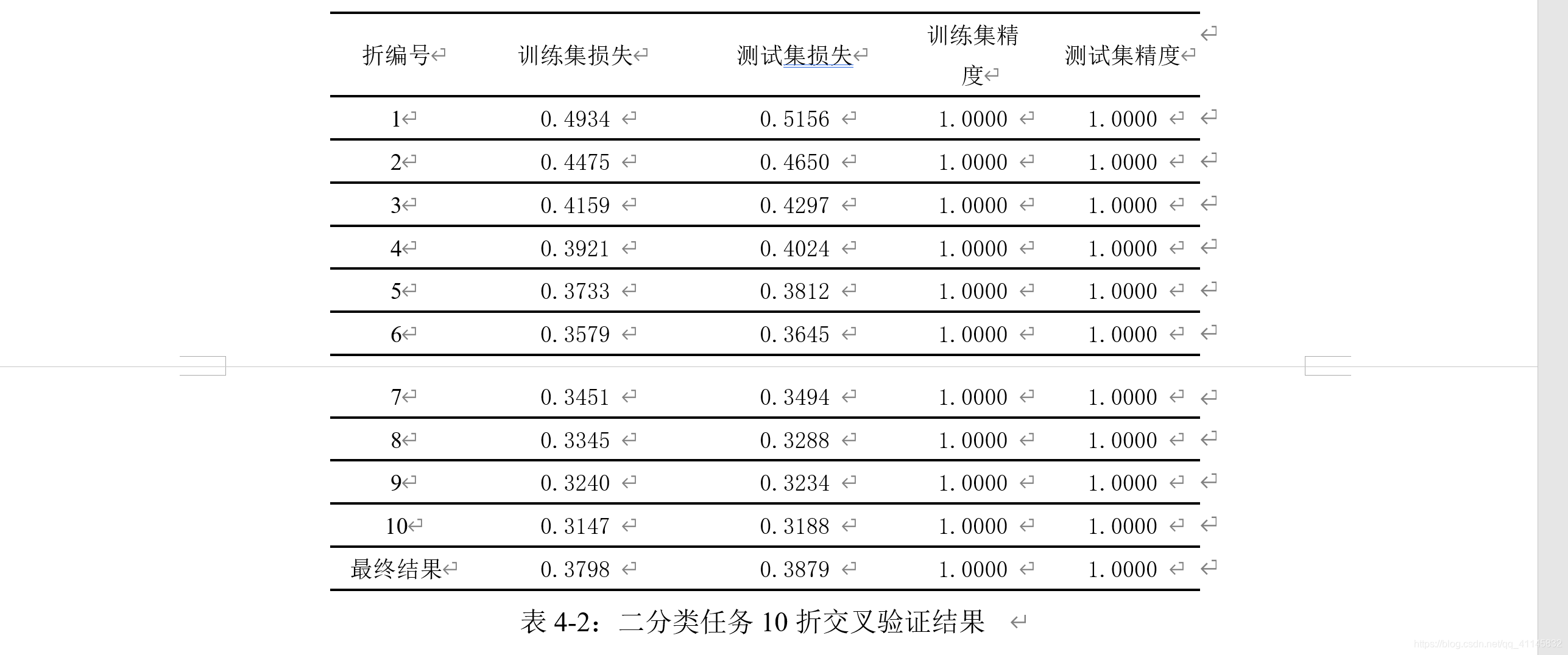
回归任务

手动实现前馈神经网络

学习率设置为1e-3，批量数为200，在Sigmoid函数激活的单层神经网络上迭代20次的结果如下：

利用torch.nn实现前馈神经网络

在torch实现的前馈神经网络上，迭代10次的结果如下：

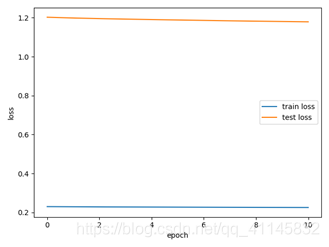
实现10折交叉验证评估

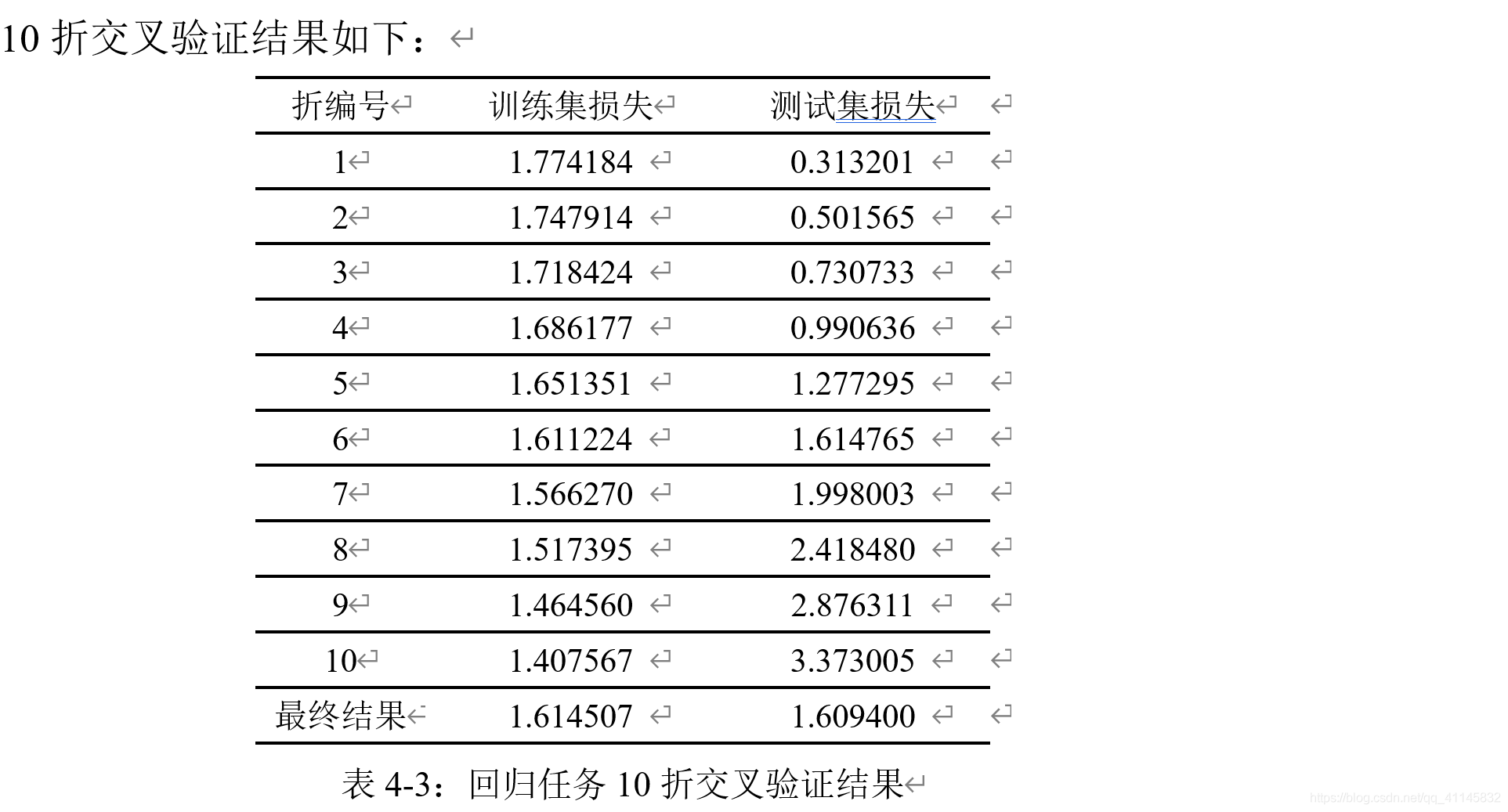
实验心得体会

本次实验中，我主要遇到了以下困难和问题：

• 对torch的索引操作不够熟练。
• 在参数调试上消耗了大量时间。
• 对于原始数据的格式问题没有引起重视，因此引发了很多的bug，消耗了大量时间。
• 没有从一开始就进行模块化设计、养成把结果数据保存以备后续使用的意识。
• 最开始计算对模型的评估时，没有去除dropout模块；后期改正之后才得到满意的结果。
  以上问题让本次实验困难重重，但都一一解决。在后续的学习中，我会重视以上问题，不断迭代更新，更熟练地完成此类程序的设计。