摘要
关于图表示学习的现有技术侧重于特定领域的问题,并为每个图数据集训练专用模型,该模型通常不可转移到域外数据。
受自然语言处理和计算机视觉中预训练最新进展的启发,我们设计了图对比编码(GCC)——一种自监督图神经网络预训练框架,用于捕获跨多个网络的通用网络拓扑特性。我们将GCC的预训练任务设计为网络内和网络间的子图实例鉴别,并利用对比学习使图神经网络能够学习内在的和可转移的结构表示。
我们在三个图学习任务和十个图数据集上进行了广泛的实验。结果表明,在不同数据集上预先训练的GCC可以实现比特定任务和从头训练的对手具有竞争力或更好的性能。这表明,预训练和微调范式对图表示学习具有很大的潜力。
1 引言
大多数图表示学习工作都集中在学习单个图或一组固定图的表示上,非常有限的工作可以转移到域外数据和任务上。本质上,这些表示学习模型旨在学习每个数据集专用的特定网络的结构模式。
基于上述局限性,本文提出以下问题:我们可以从网络中普遍地学习可转移的代表性图嵌入吗?
到目前为止,最强大的解决方案是在自监督设置下,从一个大型数据集中预先训练表示学习模型。该预训练的想法是使用预训练的模型作为良好的初始化,对看不见数据集上的(不同)任务进行微调。
理想情况下,给定一组(不同的)输入图,如脸书社交图和DBLP合著者图,我们的目标是在这些图上通过自监督任务对GNN进行预训练,然后对不同图学习任务的不同的图上的这个GNN进行微调,如美国机场图上的节点分类。
GNN预训练的关键问题是:如何设计预训练任务,以便能够捕获和进一步传输网络中和跨网络的通用结构模式?
本文提出了图对比编码(GCC)框架来学习跨图的结构表示。从概念上讲,我们利用对比学习的想法来设计图的预训练任务作为实例鉴别。
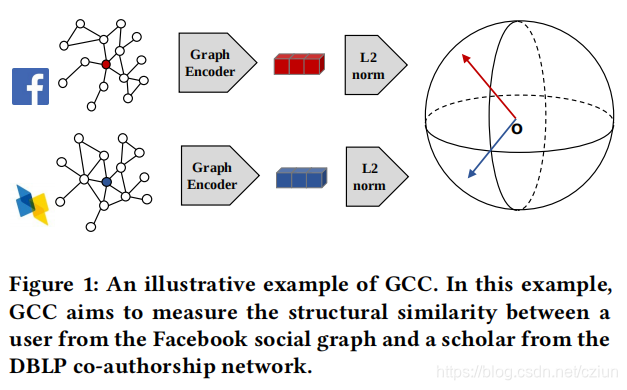
在GCC中,我们将预训练任务设计为子图实例鉴别。它的目标是根据顶点的局部结构来区分它们,如图1所示。对于每个顶点,我们从其多跳自我网络中采样子图作为实例。GCC旨在区分从某一顶点采样的子图和从其他顶点采样的子图。最后,对于每个子图,我们使用一个图神经网络(特别是GIN模型)作为图编码器,将潜在的结构模式映射到潜在表示。由于GCC不假定顶点及其子图来自同一个图,因此图编码器被迫捕获不同输入图中的通用模式。给定预先训练的GCC模型,我们将其应用于处理下游任务的看不见图。
2 GCC
图2概述了GCC的预训练和微调阶段。
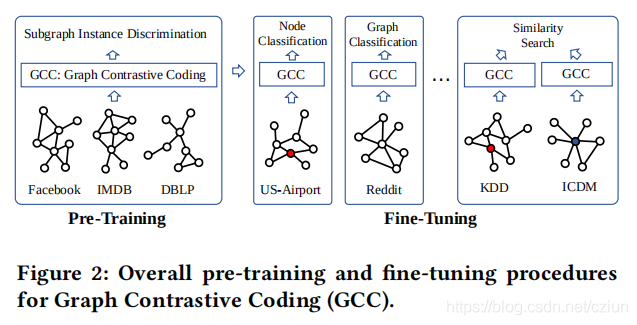
2.1 GNN预训练问题
从概念上讲,给定来自不同领域的图的集合,我们的目标是预训练GNN模型,以自监督的方式捕获这些图的结构模式。该模型应该能够使不同数据集上的下游任务受益。潜在的假设是,在不同的图中存在着共同的和可转移的结构模式。
形式上,GNN预训练问题是学习一个函数 f f f,它将一个顶点映射到一个低维特征向量,这样 f f f就具有以下两个属性:
- 结构相似性,它将具有相似局部网络拓扑的顶点映射到向量空间中彼此接近的顶点;
- 可转移性,它与训练前看不到的顶点和图兼容。
因此,嵌入函数 f f f可以用于各种图学习任务,如社会角色预测、节点分类和图分类。
请注意,这项工作的重点是没有节点属性和节点标签的结构表示学习,这使其不同于图神经网络研究中常见的问题设置。
2.2 GCC预训练
给定一组图,我们的目标是预训练一个通用的GNN编码器,以捕获这些图背后的结构模式。为了实现这一点,我们需要为图结构数据设计合适的自监督任务和学习目标。
我们将子图实例鉴别作为预训练任务,InfoNCE作为学习目标。预训练任务将每个子图实例视为自己的不同类,并学习区分这些实例。它承诺它可以输出捕获这些子图实例之间相似性的表示。
从字典查找的角度来看,给定一个编码的查询
q
\pmb{q}
q?q??q和一个包含
K
+
1
K+1
K+1编码密钥的字典
{
k
0
,
?
?
?
,
k
K
}
\{\pmb{k}_0,···,\pmb{k}_K\}
{kkk0?,???,kkkK?},对比学习查找字典中与
q
\pmb{q}
q?q??q匹配的单个密钥(由
k
+
\pmb{k}_+
kkk+?表示)。在这文中,我们采用的InfoNCE如下:
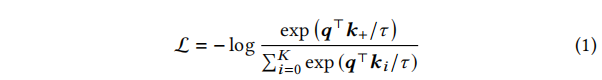
其中,
τ
τ
τ是温度超参数。
f
q
f_q
fq?和
f
k
f_k
fk?是两个图神经网络,它们分别编码查询实例
x
q
x^q
xq和每个密钥实例
x
k
x^k
xk为
d
d
d维表示,用
q
=
f
q
(
x
q
)
\pmb{q}=f_q(x^q)
q?q??q=fq?(xq)和
k
=
f
k
(
x
k
)
\pmb{k}=f_k(x^k)
kkk=fk?(xk)表示。
2.2.1 设计子图实例
对比学习框架的成功在很大程度上依赖于数据实例的定义。CV和NLP任务可以直接将实例定义为图像或句子。然而,这些想法不能明确扩展到图数据,因为图中的实例没有明确定义。此外,我们的预训练关注的纯粹是结构表示,没有额外的输入特征/属性。这使得选择单个顶点作为一个实例的情况就不可行了,因为它不适用于区分两个顶点。
为了解决这个问题,我们提出将子图作为对比实例,将每个顶点扩展到其局部结构。具体地说,对于某个顶点 v v v,我们定义了一个实例为其r-自我网络:
定义2.1【r-自我网络】 设 G = ( V , E ) G=(V,E) G=(V,E)是一个图,其中 V V V表示顶点集, E ? V × V E ? V ×V E?V×V表示边集(本文为无向边)。对于顶点 v v v,它的r-邻居被定义为 S v = { u : d ( u , v ) ≤ r } S_v=\{u:d(u,v)≤r\} Sv?={u:d(u,v)≤r},其中 d ( u , v ) d(u,v) d(u,v)是图 G G G中 u u u和 v v v之间的最短路径距离。顶点 v v v的r-自我网络,用 G v G_v Gv?表示,是由 S v S_v Sv?产生的子图。
图3的最左边部分显示了两个2-自我网络的例子。
2.2.2 定义类似/不类似的实例
在GCC中,我们将相同r-ego网络的两个随机数据增强作为一个类似的实例对,并将数据增强定义为图采样。图采样是一种从原始图中推导出具有代表性的子图样本的技术。假设我们想增强顶点 v v v的r-自我网络( G v G_v Gv?),GCC的图采样遵循三个步骤——带重启的随机游走(RWR)、子图产生和匿名化。
- Random walk with restart(带重启的随机游走)。 我们从自我顶点 v v v开始在 G G G上随机游走。游走以与边权重成比例的概率迭代地移动到其邻域。此外,在每一步中,游走以一个正的概率返回到起始顶点 v v v。
- Subgraph induction(子图产生)。 带重启的随机游走收集了 v v v周围顶点的子集,用 S ~ v \widetilde{S}_v S v?表示。然后将 S ~ v \widetilde{S}_v S v?产生的子图 G ~ v \widetilde{G}_v G v?视为r-自我网络 G v G_v Gv?的增广版本。
- Anonymization(匿名化)。 我们以任意顺序将采样图 G ~ v \widetilde{G}_v G v?的顶点重新标记为 { 1 , 2 , ? ? ? , ∣ S ~ v ∣ } \{1,2,···,|\widetilde{S}_v|\} {1,2,???,∣S v?∣},从而匿名化采样图 G ~ v \widetilde{G}_v G v?。
我们重复上述过程两次,以创建两个数据增强,它们形成一个类似的实例对 ( x q , x k + ) (x^q,x^{k_+}) (xq,xk+?)。如果两个子图从不同的r-自我网络中增强,我们将它们视为不类似的实例对 ( x q , x k ) (x^q,x^{k}) (xq,xk),其中 k ≠ k + k≠k_+ k?=k+?。
在带重启的随机游走采样中,重启概率控制着自我网络的半径(即 r r r)。在这项工作中,我们将使用0.8作为重启概率。
匿名化步骤旨在保持底层的结构模式,并隐藏精确的顶点索引。这种设计避免了学习子图实例鉴别的一个简单的解决方案,即简单地检查两个子图的顶点索引是否匹配。此外,它有助于在不同的图之间传递学习模型,因为这样的模型与特定的顶点集没有关联。
2.2.3 定义图编码器
给定两个采样子图 x q x^q xq和 x k x^k xk,GCC分别通过两个GNN编码器 f q f_q fq?和 f k f_k fk?对它们进行编码。
从技术上讲,任何GNN都可以在这里作为编码器,而GCC模型对不同的选择不敏感。在实践中,我们采用了图同构网络(GIN)作为图编码器。
回想一下,我们关注于结构表示预训练,而大多数GNN模型需要顶点特征/属性作为输入。为了弥合差距,我们利用每个采样子图的图结构来初始化顶点特征。具体来说,我们将广义位置嵌入定义如下:
定义2.2【Generalized positional embedding(广义位置嵌入)】 对于每个子图,将其广义位置嵌入定义为其归一化拉普拉斯图的顶部特征向量。形式上,假设一个子图具有邻接矩阵 A \pmb{A} AAA和度矩阵 D \pmb{D} DDD,我们对其归一化图拉普拉斯进行特征分解,满足 I ? D ? 1 / 2 A D ? 1 / 2 = U Λ U T \pmb{I}-\pmb{D}^{-1/2}\pmb{A}\pmb{D}^{-1/2}=\pmb{U}\pmb{\Lambda}\pmb{U}^T III?DDD?1/2AAADDD?1/2=UUUΛΛΛUUUT,其中 U \pmb{U} UUU的顶部特征向量定义为广义位置嵌入。
除了广义位置嵌入外,我们还添加了顶点度的one-hot编码和自我顶点的二进制指标作为顶点特征。由图编码器编码后,最终的d维输出向量用其L2-Norm进行归一化。
我们在图3中说明了一个GCC预训练的运行示例。为了简单起见,我们将字典的大小设置为3。GCC首先从图3最左部分上的一个2-自我网络中随机增加了两个子图
x
q
x^q
xq和
x
k
0
x^{k_0}
xk0?。同时,另外两个子图
x
k
1
x^{k_1}
xk1?和
x
k
2
x^{k_2}
xk2?从一个噪声分布产生——在这个例子中,它们从图3最左部分的另一个2-自我网络中随机增强。然后,两个图编码器
f
q
f_q
fq?和
f
k
f_k
fk?,将查询和三个密钥映射到低维向量
q
\pmb{q}
q?q??q和
{
k
0
,
k
1
,
k
2
}
\{\pmb{k}_0,\pmb{k}_1,\pmb{k}_2\}
{kkk0?,kkk1?,kkk2?}。最后,公式(1)中的对比损失鼓励模型将
(
x
q
,
x
k
0
)
(x^q,x^{k_0})
(xq,xk0?)识别为相似的实例对,并将其与不同的实例区分开来,即
{
x
k
1
,
x
k
2
}
\{x^{k_1},x^{k_2}\}
{xk1?,xk2?}。
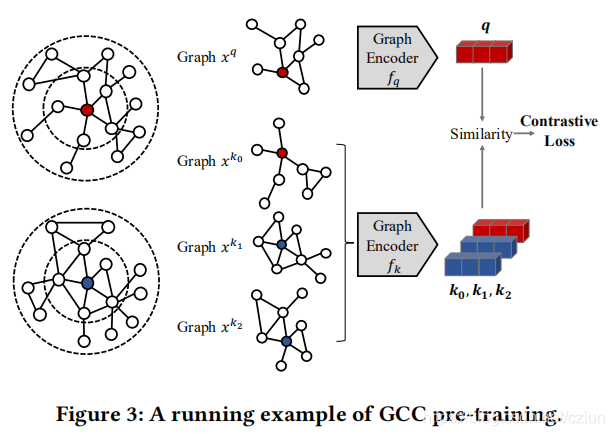
在对比学习中,需要维护
K
K
K大小的字典和编码器。理想情况下,在公式(1)中,字典应该涵盖尽可能多的实例,使
K
K
K非常大。然而,由于计算上的限制,我们通常会设计和采用经济的策略来有效地构建和维护字典,如端到端(E2E)和动量对比(MoCo)。我们将讨论以下两种策略。
E2E采样小批量的实例,并将相同小批量中的样本视为字典。然后针对 f q f_q fq?和 f k f_k fk?的参数优化等式(1)中的目标,这两个参数都可以通过反向传播一致地接受梯度更新。E2E的主要缺点是字典的大小受到批处理大小的限制。
MoCo旨在增加字典的大小,而没有额外的反向传播成本。具体地说,MoCo维护了之前小批次的样本队列。在优化过程中,MoCo只通过反向传播来更新 f q f_q fq?的参数(用 θ q θ_q θq?表示)。 f k f_k fk?的参数(用 θ k θ_k θk?表示)不通过梯度下降来更新。MoCo基于动量,通过 θ k ← m θ k + ( 1 ? m ) θ q θ_k←mθ_k+(1-m)θ_q θk?←mθk?+(1?m)θq?更新 θ k θ_k θk?,其中 m ∈ [ 0 , 1 ) m∈[0,1) m∈[0,1)是一个动量超参数。上述动量更新规则逐渐将 θ q θ_q θq?中的更新传播到 θ k θ_k θk?,使 θ k θ_k θk?平稳、一致地进化。总之,MoCo以牺牲字典一致性为代价,实现了更大的字典大小,即字典中的密钥表示是由一个平滑变化的密钥编码器进行编码的。
除了E2E和MoCo之外,还有其他的对比性学习机制来维护字典,如memory bank。我们主要关注于GCC的E2E和MoCo。
2.3 GCC微调
下游任务。 图学习中的下游任务通常分为两类:图级和节点级,其目标是分别预测图或节点的标签。对于图级任务,输入图本身可以由GCC进行编码,以实现表示。对于节点级的任务,节点表示可以通过编码其r-自我网络(或从其r-自我网络增强的子图)来定义。在这两种情况下,编码的表示随后被输入到下游任务中,以预测特定于任务的输出。
Freezing vs. full fine-tuning。 GCC为下游任务提供了两种微调策略——freezing模式和full fine-tuning模式。在freezing模式下,我们冻结预先训练的图编码器 f q f_q fq?的参数,并将其作为静态特征提取器,然后在提取的特征之上训练针对特定下游任务的分类器。在full fine-tuning模式下,将使用预先训练的参数初始化的图编码器 f q f_q fq?与分类器一起对下游任务进行端到端训练。
GCC as a local algorithm。 GCC作为一种图算法,属于局部算法类别,其中该算法只涉及输入(大规模)网络的局部探索,因为GCC通过基于随机游走的图采样方法来探索局部结构。这种特性使GCC能够扩展到大规模的图学习任务,并对分布式计算设置非常友好。
3 实验