当节点个数比较多的时候,显然直接用公式计算比较费劲了。这个时候线性代数就派上用场了,当下大部分神经网络运算其实就是矩阵的运算(这里例子是矩阵的乘积)。

上图这个神经网络省略了偏置和激活函数,只设定了权重。?
import numpy as np
X=np.array([1,2])
W=np.array([[1,3,5],[2,4,6]])
Y=np.dot(X,W)
print(Y)![]()
?这里具体来实现一个前向传播的3层神经网络:

?
实现之前,先确定一些符号,比如?, 上标3表示从第2层到第3层的权重,有时还会加括号写为(3),下标2表示后一层(当前为2-3层之间)的第2个神经元,下标4表示前一层的第4个神经元。权重按照“后一层的索引号、前一层的索引号”顺序排列。
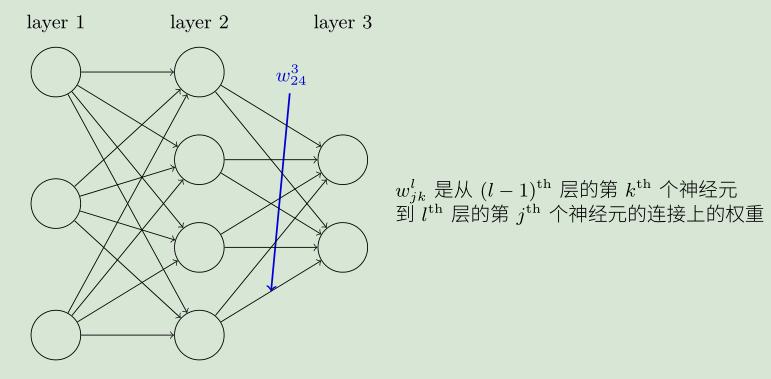
?
?现在看下从输入层到第一层的第一个神经元的信号传递过程:

上图中,1是表示偏置的神经元,这里偏置的右下角标索引只有一个是因为前一层的神经元只有1个,偏置权重的数量取决于后一层的神经元数量。
图中,, 同样地,
...
用线性代数的矩阵乘法运算可以表示为:
用Python实现一下:
import numpy as np
import sigmoid
X=np.array([1,2])
W1=np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
B1=np.array([0.1,0.2,0.3])
A1=np.dot(X,W1)+B1
Z1=sigmoid.sigmoid(A1)
print(A1)
print(Z1)?输出结果:
![]()
?代码部分,我们用了sigmoid激活函数使得
,这个激活函数的计算过程表示了隐藏层的加权和(包括加权信号和偏置的总和,用
表示)被激活转换后的信号(用
表示)

?下面实现从第1层到第2层的信号传递,如上图所示。
W2=np.array([[0.1,0.3],[0.2,0.4],[0.3,0.5]])
B2=np.array([0.2,0.3])
A2=np.dot(Z1,W2)+B2
Z2=sigmoid.sigmoid(A2)?最后,实现从第2层到输出层的信号传递。
W3=np.array([[0.2,0.4],[0.3,0.5]])
B3=np.array([0.3,0.4])
A3=np.dot(Z2,W3)+B3?这里没用sigmoid作为输出的激活函数,而是直接按照加权和输出,这种形式叫做恒等函数作为(输出层的)激活,通常输出层的激活函数为了区别于隐藏层激活函数,会用表示。
print(A1,A2,A3) print(Z1,Z2)
出来后的结果是:
![]()
关于最后输出层激活函数的使用,要根据求解问题的性质确定的。通常,回归问题用恒等函数,二分类问题用sigmoid函数,多分类问题用softmax函数。
以上代码定义函数优化后:
import numpy as np
import sigmoid
def initial_network():
network={} #用字典来存权重
network['W1'] = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]]) #字典Key就是权重名字
network['B1'] = np.array([0.1,0.2,0.3])
network['W2'] = np.array([[0.1,0.3],[0.2,0.4],[0.3,0.5]])
network['B2'] = np.array([0.2,0.3])
network['W3'] = np.array([[0.2,0.4],[0.3,0.5]])
network['B3'] = np.array([0.3,0.4])
return network
def identity_function(x):
return x
def forward(network,x):
W1, W2, W3=network['W1'], network['W2'], network['W3']
B1, B2, B3=network['B1'], network['B2'], network['B3']
A1=np.dot(X,W1)+B1
Z1=sigmoid.sigmoid(A1)
A2=np.dot(Z1,W2)+B2
Z2=sigmoid.sigmoid(A2)
A3=np.dot(Z2,W3)+B3
Y=identity_function(A3)
return Y
network=initial_network()
X=np.array([1,0.5])
Y=forward(network,X)
print(Y) #[0.65577234 1.03624354]?
?
?
?
?
?
?
?
?