简单理解回归

回归有线性回归和非线性回归，线性回归字面意思就是散点呈现出一条类似于直线，非线性则为光滑曲线。回归有一个因变量和一个或多个自变量组成，一个自变量则是单变量回归，多个自变量则是多变量回归。
回归可以用来预测价格或者某种东西的趋势，总之来说是连续型的。
逻辑回归感觉其实不像是我们所理解的大多数情况下的回归，它又可以认为是一种微分方程，但又是一种对数线性模型，因为逻辑回归是处理二分类问题，因变量输出的是0或1，这是因为逻辑回归中存在一个 $s i g m o i d$ 函数，这个函数起来的就是可以用概率分类的作用。而其实实际上，在这个 $s i g m o i d$ 函数中 $z$ 就是作为一个线性回归函数。
$y=\frac{1}{1+e^{-z}}$
其中可以将 $z$ 建立为 $z=\alpha_0+\alpha_1x_1+\alpha_2x_2+\varepsilon_i$ ， $z$ 可以是多变量回归函数也可以是单变量回归函数。

机器学习中的回归问题处理

简单写下我自己在机器学习中的对于回归问题的处理，如果中间有一些错误，恳请各位前辈指出。

回归问题中的数据需要带有标签的数据集，即为有监督学习。
划分数据集，自己习惯按8:2划分训练集和测试集，注意需要划分完训练集后对训练集进行标准化处理，因为数据集中每一个维度的数据单位有所不同，所以需要进行标准化处理。至于为什么需要在划分完数据集后再进行对训练集进行处理而不对测试集进行处理，这是为了减少在机器学习中数据泄露而出现过拟合问题。
选择特征维度，这一步非常关键，可以说是决定了模型的优良问题。在这一步上需要进行特征工程。对于多维度数据集可以使用PCA主成分或者因子降维等方法，或者计算维度之间的协方差或者皮尔逊相关系数等，在这一阶段使用的方法有很多，可以选择我们自身想要研究的影响因素作为特征维度也可以通过上面等方法选择各个维度之间相关性较强的维度等等。
最后通过sklearn库调用函数进行构建模型以及训练模型，再代入测试集进行检验模型，通常我自己习惯使用AUC指标和ROC指标对模型进行检验。
举一个小栗子：

实战

之前建立过顾客消费行为机器学习模型，通过顾客对产品各个维度的评分数据进行预测顾客是否消费。以及建立过二手房价预测模型，显然前者是一个二分类问题，后者是一个回归问题，总体大类上还是属于监督学习。
下面展示下构建了逻辑回归、树模型对顾客消费行为进行预测：

import pandas as pd
import matplotlib.pyplot as plt
# 划分数据
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import MinMaxScaler
# 逻辑回归
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
from sklearn import metrics
# xgboost
import xgboost as xgb
# 保存模型
import joblib
plt.rcParams["font.family"] = "SimHei"          # 设置可以显示中文字体
plt.rcParams["axes.unicode_minus"] = False   

data = pd.read_excel('数据.xlsx',sheet_name='3') # 导入预处理完的数据集
y = data['购买意愿'].values
X=data.iloc[:, 0:25].values
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size= 0.2,random_state=30) # 划分数据集

# 标准化
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test) 

lr = LogisticRegression()                                        # 构建逻辑回归模型
lr.fit(X_train,y_train)                                          # 训练模型
y_prob = lr.predict_proba(X_test)[:,1]                           # 购买行为概率预测
y_pred = lr.predict(X_test)                                      # 对测试集的预测结果
fpr_lr,tpr_lr,threshold_lr = metrics.roc_curve(y_test,y_prob)    # 真阳率、伪阳率、阈值
auc_lr = metrics.auc(fpr_lr,tpr_lr)                              # AUC得分
score_lr = metrics.accuracy_score(y_test,y_pred)                 # 模型准确率
print('模型准确率为:{},AUC得分为:{}'.format(score_lr,auc_lr))
print('------------------------------------------------------------')
print(classification_report(y_test,y_pred,labels=None,target_names=None,sample_weight=None, digits=2))

结果：
在这里插入图片描述
保存模型，便于对需要预测的数据集进行预测：

joblib.dump(lr,'save/model1.pkl')
df_1 = pd.read_excel('预测.xlsx')
X = df_1.drop(['购买意愿'],axis=1)
m_1 = joblib.load('save/model1.pkl')
name_list1 = []
# 预测
to_list1 = m_1.predict(X)
for i in to_list1:
    name_list1.append(i)
# 赋值
df_1['购买意愿'] = name_list1
df_1.to_excel('预测成功.xlsx',encoding='utf-8') # 保存结果

树模型（前面标准化处理及以上步骤一致，即只展示模型构建过程代码）：

# 读入训练集和测试集
dtrain=xgb.DMatrix(X_train,y_train)
dtest=xgb.DMatrix(X_test)
 
# 参数
params={'booster':'gbtree','objective': 'binary:logistic','eval_metric': 'auc',
    'max_depth':8,'gamma':0,'lambda':2,'subsample':0.7,'colsample_bytree':0.8,
    'min_child_weight':3,'eta': 0.2,'nthread':8,'silent':1}
 
# 模型训练
watchlist = [(dtrain,'train')]
bst=xgb.train(params,dtrain,num_boost_round=500,evals=watchlist)
 
# 预测为正类的概率
y_prob=bst.predict(dtest)
 
# 设置阈值为0.5
y_pred = (y_prob >= 0.5)*1
 
# 真阳率、伪阳率、阈值
fpr_xgb,tpr_xgb,threshold_xgb = metrics.roc_curve(y_test,y_prob)   
auc_xgb = metrics.auc(fpr_xgb,tpr_xgb)    # AUC得分
score_xgb = metrics.accuracy_score(y_test,y_pred)    # 模型准确率
print('模型准确率为:{},AUC得分为:{}'.format(score_xgb,auc_xgb))
print('-------------------------------------------------------------')
print(classification_report(y_test,y_pred,labels=None,target_names=None,sample_weight=None, digits=2))

运行结果：
在这里插入图片描述
保存模型与上面逻辑回归一致，即不再重复。
以上是离散型变量，在特征工程过程的特征维度选择中使用的是PCA主成分降维算法。而对于连续型变量中房价预测问题，sklearn有一个非常经典的波斯顿房价的数据集。
在这里插入图片描述

不使用sklearn构建回归模型

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

x = [1.385,1.221,1.123,1.065,0.954] 
x = np.reshape(x,newshape=(5,1))
y =  [2.133, 2.016, 1.913, 1.862, 1.801] 
y = np.reshape(y,newshape=(5,1)) 

# 一元线性函数
def model(a, b, x):
    return a*x + b
# 损失函数
def cost(a, b, x, y):
    n = 5
    return 0.5/n * (np.square(y-a*x-b)).sum()
# 梯度下降函数
def time(a,b,x,y):
    n = 5
    alpha = 1e-1
    y_hat = model(a,b,x)
    aa = (1.0/n) * ((y_hat-y)*x).sum()
    bb = (1.0/n) * ((y_hat-y).sum())
    a = a - alpha*aa
    b = b - alpha*bb
    return a, b
# 初值
a=0
b=0
# 迭代次数
def train(a,b,x,y,times):
    for i in range(times):
        a,b = time(a,b,x,y)

    y_hat=model(a,b,x)
    cost_f = cost(a, b, x, y)
    print(a,b,cost_f)
    plt.scatter(x,y)
    plt.plot(x,y_hat)
    return a,b
a,b = iterate(a,b,x,y,1000)
# R方
y_hat=model(a,b,x)
y_bar = y.mean()
SST = np.square(y - y_bar).sum()
SSR = np.square(y_hat - y_bar).sum()
SSE = np.square(y_hat - y).sum()
R_Square = SSR/SST
R_Square

结果：
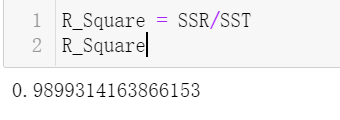
在这里插入图片描述

说明：代码里面的损失函数就是最小二乘，梯度下降作用使得损失函数取最小值。

回归模型的最小二乘

回忆一下课本上最小二乘的知识，
在这里插入图片描述

粗暴的讲就是真实值和预测值之间的差距，要使残差平方和最小。

线性回归中，极大似然估计与最小二乘联系与区别

最小二乘：估计值和观测值之差的平方和最小。
极大似然：参数估计量应该使得从模型中抽取该n组样本观测值的概率最大，就是概率分布函数或似然函数最大。
区别：

极大似然需要已知概率分布函数，实践中难以获得。
最小二乘法以估计值与观测值的差的平方和作为损失函数，极大似然法则是以最大化目标值的似然概率函数为目标函数。
联系：
最小二乘的解析解可以用Gaussian分布以及最大似然估计求得。
，在假设满足正态分布的情况下，两者是等价的。

多项式回归在实际问题中表现经常不是很好

多项式回归中曲线就越光滑使得边界处的置信区间增大，即减低了预测效果。
在这里插入图片描述
实线为真实值，两侧曲线为置信区间。

决策树模型与线性模型之间的联系和区别

决策树：

在训练过程中，需要计算特征属性的信息增益或信息增益率等度量，从而确定哪个属性对目标最有益，即有最强区分样本的能力。
特征空间复杂，无法用线性表达时使用树模型来解决问题。
线性模型：
线性模型是对所有特征赋予权重后相加得到一个新的值。
在训练过程中，线性模型使用简单公式通过一组数据点找到最佳拟合。

区别：

线性模型容易受极值影响，而决策树在这方面较好。
线性模型较为简单，不容易产生过拟合。决策树容易产生过拟合，通常通过剪枝避免产生过拟合。
联系：
2014年faceBook提出了树模型GBDT与线性模型LR的融合模型，利用GBDT构造有效的交叉特征，从根节点到叶子节点的路径，代表部分特征组合的一个规则，提升树将连续特征转化为离散特征，可以明显提升线性模型的非线性表达能力，提高线性模型精度。参考通道~~~~~~~~~~~~~~~~