[人工智能]2021-08-19

1.1 模型-策略-算法

1. 模型：在假设空间中，模型一般有无穷多个；

   • 生成式模型：通过数据学习联合概率分布P(X,Y)，然后求出条件概率分布P(Y|X) = P(X,Y) / P(X)作为预测模型。

     • 强调：输入X和输出Y之间的关系；
     • 模型：朴素贝叶斯模型、隐马尔可夫模型和高斯混合模型等。

   • 判别式模型：通过数据直接学习决策函数P(Y)或者条件概率分布P(Y|X)作为预测模型。

     • 强调：给定输入X，应该得到什么样的输出Y。
     • 模型：K近邻算法、感知机、决策树、逻辑回归、最大熵模型、支持向量机、提升算法、神经网络和条件随机场等。

     生成式模型	判别式模型
     假设	满足一些假设 条件独立性假设、混合高斯分布
     生成	生成样本
     速度	更容易拟合数据
     误差	较高
     新类	不需要全部样本重新训练

2. 策略：按照什么样的规则选择最优模型；

   • 损失函数：一次预测的好坏。
     • 0-1损失函数：
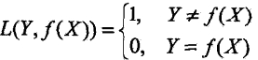
     • 平方损失函数：
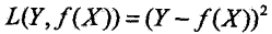
     • 对数损失函数：
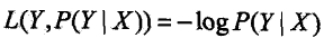
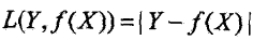
     • 绝对值损失函数：
   • 风险函数：整体预测的好坏。
     • 期望风险：模型关于联合概率分布P(x,y)的期望损失。联合概率分布未知的&无法学习；
     • 经验风险：模型关于训练集的平均损失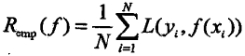，根据大数定律，当样本量N趋于无穷时，经验风险趋于期望风险，但现实中训练样本有限，可能出现过拟合现象；
     • 结构风险：为防止过拟合提出的策略。 等价于 经验风险 + 正则化项(模型复杂度)。
   • 目标函数：通常指结构风险最小化函数。

3. 算法：求解最优化问题的方法。

1.2 正则化

• 定义：模型参数向量的范数。
• 范数：矩阵范数（矩阵变化的大小）、向量范数（向量大小）。
  • L₀范数：是指向量中非0的元素的个数。
  • L₁范数：是指向量中各个元素绝对值之和：
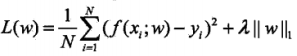
  • L₂范数：是指向量各元素的平方和然后开方：

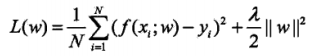
1.3 误差

• 训练误差：模型在训练集上的平均损失；
• 测试误差：模型在测试集上的平均损失；
• 泛化误差：模型对未知数据的预测能力，常用测试误差来预计。

1.4 过拟合与欠拟合

• 过拟合：模型复杂度较高，训练误差小，测试误差大。

  • 添加其他特征项。比如：组合特征；
  • 添加多项式特征。比如：二次项或者三次项特征；
  • 减少正则化参数。正则化用于防止过拟合的；

• 欠拟合：模型复杂度较低，训练误差大，测试误差大。

  • 增大数据集。估计参数分布并生成新样本；数据增强（比如：图像的旋转，平移或缩放）
  • 添加正则化项。L0正则、L1正则、L2正则等。
  • 采用dropout方法。模型训练时随机让某些隐含层节点的权重不参与计算。

1.5 模型评估方法

• 留出法：

  • 场景：样本充足时，数据集D划分训练集S，测试集T。
  • 要求1：数据分布一致，比如：采用分层采样保证类别比例相似。
  • 要求2：单次评估结果不稳定，重复评估取均值。
  • 要求3：训练集S太大，评估结果方差大；测试集T太大，评估结果偏差大。因此，大约2/3 ~ 4/5的样本用于训练，剩余样本用于测试；
  • 缺点：保留一部分样本做测试集，模型在非全量数据上训练可能存在偏差。

• 交叉验证法：

  • 场景：样本量不足时
  • 要求1：分层采样将训练集D划分成k份数据分布相似的互斥子集D_i=0-k；一份数据做测试，剩余做训练。k折交叉验证
  • 要求2：随机划分p次，取p次k折交叉验证结果的均值。p次k折交叉验证
  • 缺点：保留了一部分样本做测试集，模型在非全量数据上训练可能存在偏差。

• 留一法：交叉验证法的个例（k=总样本量m）。

  • 场景：样本量不足时；
  • 优点：不受随机划分影响，模型更准确（1个样本之差）；
  • 缺点：数据量太大时，计算开销大；

• 自助法：避免上述3中方法的缺点而来

  • 场景：样本量不足时；

  • 要求：采用**自助采样法（boostrap sampling）**有放回随机采样m次生成训练集D^’，剩余做测试集。**36.8%**的样本没有出现在训练集中：

    

  • 优点：类似于集成学习，有利于训练好的模型；

  • 缺点：训练集改变了初始数据集的分布，引入了偏差。

1.6 性能度量

• 回归问题：均方误差

  

• 二分类问题：

  • 错误率：分类错误的样本数 / 样本总数；

  • 精 度：分类正确的样本数 / 样本总数；

  • 查准率：准确率（Precision）= TP / (TP+FP)。

  • 查全率：召回率（Recall）= TP / (TP+FN)。

  • PR曲线：根据测试结果对样本排序，最前面“最有可能”是正例的样本。逐个把样本作为正例计算出当前的“查准率”和“查全率”。性能评价：完全包裹法、曲线面积、平衡点法

    

  • F₁值： 查准率和查全率的调和均值（又称倒数平均数：各变量倒数的平均数的倒数）

    

  • F_β值：加权调和均值。当0<β<1时：偏重查准率；当β>1时：偏重查全率；

    

  • ROC曲线：受测试者工作特征曲线。排序并逐个将样本作为正类计算：

    

  • AUC值：ROC曲线下的面积

    

• 多分类问题：

  • 思路1：每两两类别计算出查准率和查全率(P₁，R₁), (P₂，R₂)…(P_n，R_n)；再分别计算PR均值，宏查准率(macro-P)、宏查全率(macro-R)。最后计算宏F₁(macro-F₁)。
    • 思路2：先计算所有TP、FP、TN、FN的均值，再分别计算微查准率(micro-P)、微查全率(micro-R)，最后计算微F₁(micro-F₁)。

1.7 假设检验

• 假设检验的目的：从统计学的角度，判断不同算法的性能是否存在显著差异。

• 交叉验证 t 检验：又称成对 t 检验。

  • 思想：根据成对算法性能差值的均值和方差计算服从 t 分布的随机变量 t ，根据自由度、 t 分布临界值表判断性能是否存在差异；
  • 服从：t 分布；
  • 场景：两两算法在相同数据集上的两两比较。

• Friedman检验：

  • 思想：根据不同算法在不同数据集上的性能表现进行排序得到序值表，再计算服从卡方分布的随机变量，根据算法个数、数据集个数、 F分布的临界值表判断性能是否存在差异；
  • 服从：卡方分布（原始）、F分布（修正）；
  • 场景：多个算法在多个数据集上进行比较。

1.8 偏差与方差

• 泛化误差：由偏差、方差和噪声组成：

  

  • 偏差：度量算法的期望预测与真实结果的偏离程度；刻画算法本身的拟合能力；

  • 方差：度量相同规模数据集变动所导致的性能变化；刻画数据扰动造成的影响；

  • 噪声：度量当前任务上所有算法的泛化误差的下界；刻画任务本身的难易程度；

• 泛化性能：由算法能力、数据是否充分和问题难度共同决定。

• 偏差方差关系：

  
  • 训练不足时，拟合能力不足，训练集变化导致拟合能力变化不显著；偏差主导泛化错误率；
  • 训练充足时，拟合能力很强，训练集微小变化导致拟合能力发现显著变化，容易导致了过拟合。