1.研究背景??
在绝大多数目标检测网络中,如下图Fig1特征金字塔(Feature Pyramid Network,FPN)是一个不可缺少的部分,FPN网络主要解决的问题是目标检测在处理多尺度变化问题的不足。FPN主要有以下两个作用:1)多尺度特征融合,提高了特征的丰富程度;2)使用分治法,将目标检测任务按照目标尺寸不同,分成若干个检测子任务。
?

2.存在的问题?
在检测分支当中低层特征适合检测图片中的小物体,高层特征适合检测图片中的大物体,中间层特征适合检测图片中的中等大小物体。而在FPN中采用的是concatenate或者element-wise这种直接拼接或者直接相加的方式,作者认为这样并不能充分利用不同尺度的特征。提出一种新的融合方式来替代concatenate或element-wise。
3.ASFF
3.1 网络结构
针对以上存在的问题,作者提出了如下图Fig2提出的ASFF自适应特征融合方式,图中以ASFF-3为例,图中的绿色虚线框中描述了文中提出的特征融合,
,
分别来自level-1,level-2,level-3的特征,将不同层的特征乘上相应的可学习权重
,?
,?
并相加得到新的融合特征ASFF-3,其中
,
,
是第
层特征图学习到的参数,其中
为下式(
,
,
为?
,
,
经过1×1卷积得到的):
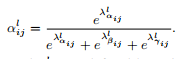
?同时三个参数需要满足以下两个条件:

?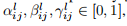
最终在第层的输出结果为:
?=?
?+?
?+?

3.2 梯度计算
文中以level-1层的feature map上的点(i,j)为例,其梯度如下面的公式1所示:
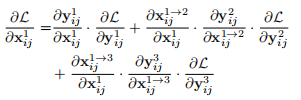
由于文中使用的是插值进行上采样,使用池化进行下采样,所以这里将这样上述公式1就简化为下面的公式2:

因为在Yolov3或者RetinaNet上对于特征融合的部分是element-wise或者concatenate,所以等于一个常数,同理
也是一个常数,所以将其简化为1。那么公式2又简化为下面的公式3:
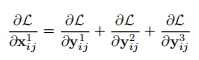
文中讲假设在level-1特征层上的点(i,j)位置上存在正样本,那么就为正样本梯度,那么其他level特征层上的点(i,j)位置上就被看作为背景的负样本,其梯度为负样本的梯度,这种不一致性(在反向传播中既包含负样本也包含正样本)会对梯度造成影响,而且也会降低训练效率。而文中提出的ASFF模块的方式的反向传播的表达式为下面的公式4:
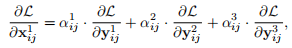
在公式4中可以通过控制参数∈[0, 1]来实现,如果
,
?= 0那么在点(i,j)上的负样本的梯度就不会干扰正样本的梯度。
4.实验
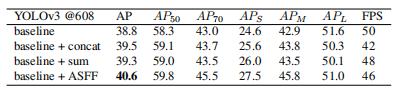
从下图Fig3中可以看出在使用了ASFF模块后会比使用concat和sum的AP值有所提升。
从下图Fig4中可以看出图中所有的斑马都是由level-1层的特征图来预测的。这就说明了斑马的中心区域在level-1层预测,level-2,level-3层被过滤掉了。

从下图Fig5中可以看出网球拍虽然是在level-1里面预测,但是其中心区域的内的主要特征来自level-2,作者推测,虽然网球拍是从level-1被预测出来的,但来自level-2的特征在检测它时更具鉴别性,因为它们包含了更丰富的线条和形状的线索。

?上图Fig6为Yolov3+ASFF模块网络与其他one-stage和two-stage网络的一个AP的比较。