论文名称:CCNet: Criss-Cross Attention for Semantic Segmentation
作者:Zilong Huang,Xinggang Wang Yun,chao Wei,Lichao Huang,Wenyu Liu,Thomas S. Huang
Code:https://github.com/speedinghzl/CCNet
摘要
上下文信息在视觉理解问题中至关重要,譬如语义分割和目标检测;
本文提出了一种十字交叉的网络(Criss-Cross Net)以非常高效的方式获取完整的图像上下文信息:
- 对每个像素使用一个十字注意力模块聚集其路径上所有像素的上下文信息;
- 通过循环操作,每个像素最终都可以捕获完整的图像相关性;
- 提出了一种类别一致性损失来增强模块的表现。
CCNet具有一下优势:
- 显存友好:相较于Non-Local减少显存占用11倍
- 计算高效:循环十字注意力减少Non-Local约85%的计算量
- SOTA
- Achieve the mIoU scores of 81.9%, 45.76% and 55.47% on the Cityscapes test set, the ADE20K validation set and the LIP validation set respectively
介绍
- 当前FCN在语义分割任务取得了显著进展,但是由于固定的几何结构,分割精度局限于FCN局部感受野所能提供的短程感受野,目前已有相当多的工作致力于弥补FCN的不足,相关工作看论文。
- 密集预测任务实际上需要高分辨率的特征映射,因此Non-Local的方法往往计算复杂度高,并且占用大量显存,因此设想使用几个连续的稀疏连通图(sparsely-connected graphs)来替换常见的单个密集连通图( densely-connected graph),提出CCNet使用稀疏连接来代替Non-Local的密集连接。
- 为了推动循环十字注意力学习更多的特征,引入了类别一致损失(category consistent loss)来增强CCNet,其强制网络将每个像素映射到特征空间的n维向量,使属于同一类别的像素的特征向量靠得更近。
方法
CCNet可能是受到之前将卷积运算分解为水平和垂直的GCN以及建模全局依赖性的Non-Local,CCNet使用的十字注意力相较于分解更具优势,拥有比Non-Local小的多得计算量。
文中认为CCNet是一种图神经网络,特征图中的每个像素都可以被视作一个节点,利用节点间的关系(上下文信息)来生成更好的节点特征。
最后,提出了同时利用时间和空间上下文信息的3D十字注意模块。
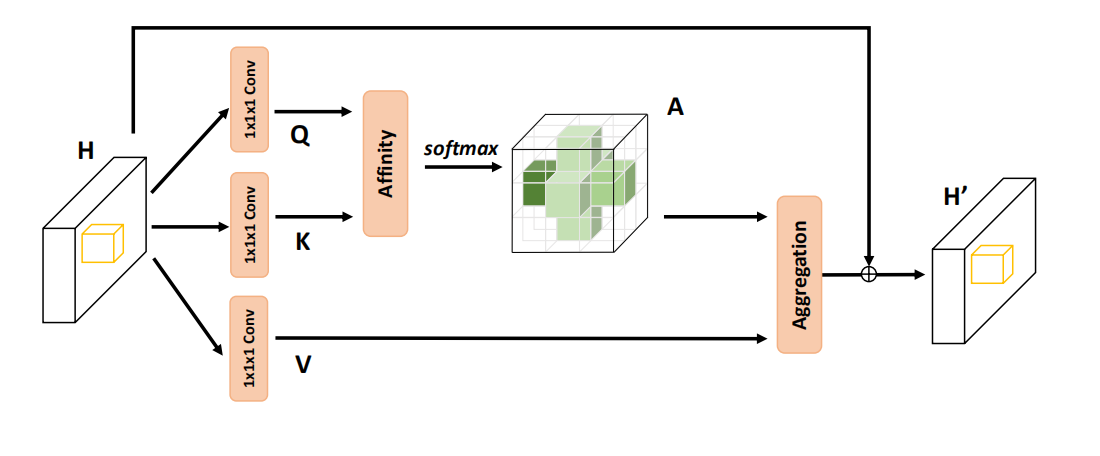
网络结构
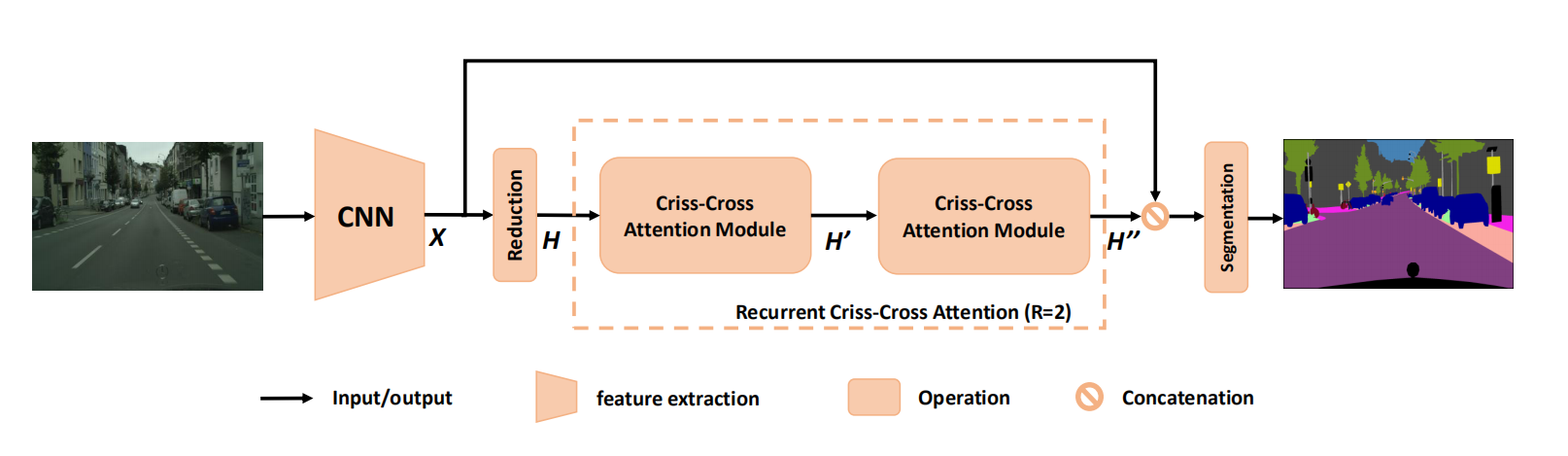
整体流程如下:
- 对于给定的 X X X,使用卷积层获得降维的特征映射 H H H;
- H H H会输入十字注意力模块以生成新的特征映射 H ′ H' H′?,其中每个像素都聚集了垂直和水平方向的信息;
- 进行一次循环,将 H ′ H' H′输入十字注意力,得到 H ′ ′ H'' H′′,其中每个像素实际上都聚集了所有像素的信息;
- 将 H ′ ′ H'' H′′与局部特征表示 X X X进行 C o n c a t e n a t i o n Concatenation Concatenation??;
- 由后续的网络进行分割。
Criss-Cross Attention
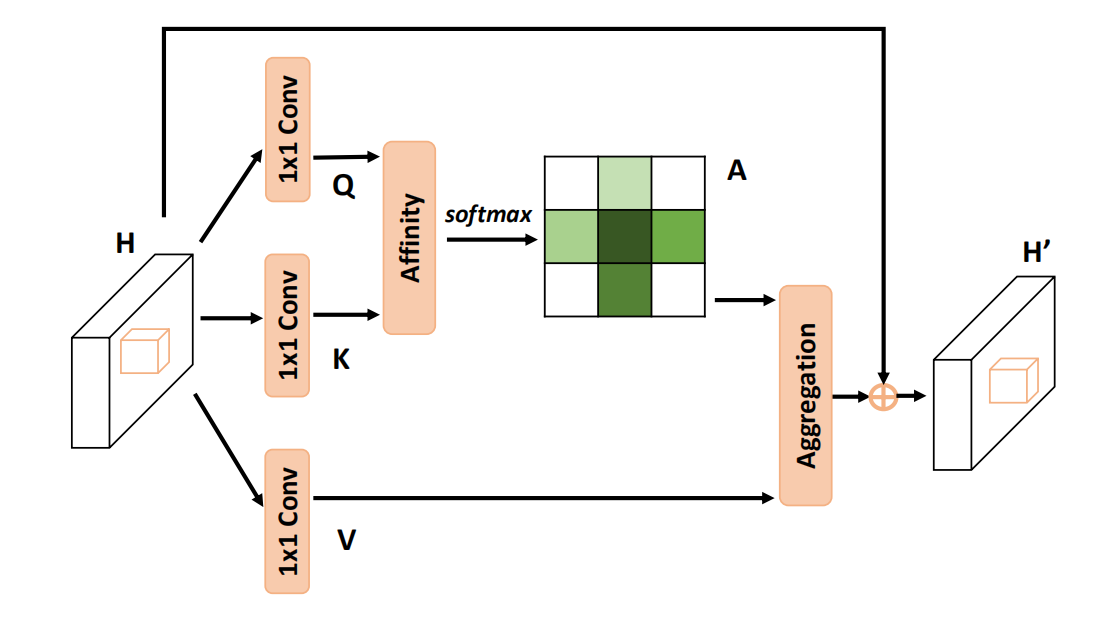
主要流程如下:
-
使用 1 × 1 1\times 1 1×1?卷积进行降维得到 Q , K ∈ R C ′ × W × H Q,K \in \mathbb{R}^{C' \times W\times H} Q,K∈RC′×W×H?;
-
通过Affinity操作生成注意力图 A ∈ R ( H + W ? 1 ) × ( H × W ) A\in\mathbb{R}^{(H+W-1)\times (H\times W)} A∈R(H+W?1)×(H×W)?,其中:
-
对于 Q Q Q?空间维度上的的每一个位置 u u u?,我们可以得到一个向量 Q u ∈ R C ′ Q_u\in\mathbb{R}^{C'} Qu?∈RC′?;???
-
同时,我们在 K K K?上得到一个集合 Ω u ∈ R ( H + W ? 1 ) × C ′ \Omega_u \in \mathbb{R}^{(H+W-1) \times C'} Ωu?∈R(H+W?1)×C′??,其代表着位置 u u u???的同一行或同一列;
-
令 Ω i , u \Omega_{i,u} Ωi,u??表示 Ω u \Omega_{u} Ωu??的第 i i i个元素,Affinity操作可以表示为:
d i , u = Q u Ω i , u T i ∈ [ 0 , 1 , ? ? , H + W ? 1 ] , u ∈ [ 0 , 1 , ? ? , H × W ] d_{i,u}=Q_u\Omega_{i,u}^T\qquad i\in [0,1,\cdots,H+W-1],u\in[0,1,\cdots,H\times W] di,u?=Qu?Ωi,uT?i∈[0,1,?,H+W?1],u∈[0,1,?,H×W]
其用来表示两者之间的相关性,最终我们可以得到 D ∈ R ( H + W ? 1 ) × ( H × W ) D\in\mathbb{R}^{(H+W-1)\times (H\times W)} D∈R(H+W?1)×(H×W)?? -
最终在通道维度上对 D D D?使用 S o f t m a x Softmax Softmax?,即可得到注意力图 A A A?,需要注意的是,这里的通道维度代表的是 H + W ? 1 H+W-1 H+W?1????这个维度,其表示某个位置像素与其垂直水平方向上像素的相关性。
-
-
另一方面,依旧使用 1 × 1 1\times 1 1×1卷积生成 V ∈ R C × W × H V \in \mathbb{R}^{C \times W \times H} V∈RC×W×H,我们可以获得一个向量 V u ∈ R C V_u\in \mathbb{R}^C Vu?∈RC和一个集合 Φ u ∈ R ( H + W ? 1 ) × C \Phi_u\in \mathbb{R}^{(H+W-1)\times C} Φu?∈R(H+W?1)×C?
-
最后使用Aggregation操作得到最终的特征图,其定义为:
H u ′ = ∑ i = 0 H + W ? 1 A i , u Φ i , u + H u H'_u=\sum_{i=0}^{H+W-1}A_{i,u}\Phi_{i,u}+H_u Hu′?=i=0∑H+W?1?Ai,u?Φi,u?+Hu?
其中 H u ′ ∈ R C H'_u\in\mathbb{R}^{C} Hu′?∈RC???是某个位置的特征向量。
至此,我们已经能够捕获某个位置像素水平和垂直方向上的文本信息,然而,该像素与周围的其他像素仍然不存在关系,为了解决这个问题,提出了循环机制。
Recurrent Criss-Cross Attention (RCCA)
通过多次使用CCA来达到对上下文进行建模,当循环次数R=2时,特征图中任意两个空间位置的关系可以定义为:
?
i
∈
R
H
+
W
+
1
,
s
.
t
.
A
i
,
u
=
f
(
A
,
u
x
C
C
,
u
y
C
C
,
u
x
,
u
y
)
\exist i\in\mathbb{R}^{H+W+1},s.t.A_{i,u}=f(A,u_{x}^{CC},u^{CC}_y,u_x,u_y)
?i∈RH+W+1,s.t.Ai,u?=f(A,uxCC?,uyCC?,ux?,uy?)
方便起见,对于特征图上的两个位置
(
u
x
,
u
y
)
(u_x,u_y)
(ux?,uy?)和
(
θ
x
,
θ
y
)
(\theta_x,\theta_y)
(θx?,θy?),其信息传递示意图如下:
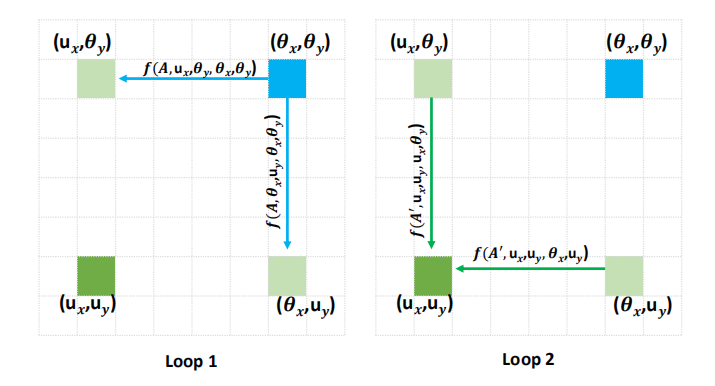
可以看到,经过两次循环,原本不相关的位置也能够建立联系了。
Learning Category Consistent Features
对于语义分割任务,属于同一类别的像素应该具有相似的特征,而来自不同类别的像素应该具有相距很远的特征。
然而,聚集的特征可能存在过度平滑的问题,这是图神经网络中的一个常见问题,为此,提出了类别一致损失。
l
v
a
r
=
1
∣
C
∣
∑
c
∈
C
1
N
c
∑
i
=
1
N
c
φ
v
a
r
(
h
i
,
μ
i
)
l_{var}=\frac{1}{|C|}\sum_{c\in C}\frac{1}{N_c}\sum_{i=1}^{N_c}\varphi_{var}(h_i,\mu_i)
lvar?=∣C∣1?c∈C∑?Nc?1?i=1∑Nc??φvar?(hi?,μi?)
l d i s = 1 ∣ C ∣ ( ∣ C ∣ ? 1 ) ∑ c a ∈ C ∑ c b ∈ C φ d i s ( μ c a , μ c b ) l_{dis}=\frac{1}{|C|(|C|-1)}\sum_{c_a\in C}\sum_{c_b\in C}\varphi_{dis}(\mu_{c_a},\mu_{c_b}) ldis?=∣C∣(∣C∣?1)1?ca?∈C∑?cb?∈C∑?φdis?(μca??,μcb??)
l r e g = 1 ∣ C ∣ ∑ c ∈ C ∣ ∣ μ c ∣ ∣ l_{reg}=\frac{1}{|C|}\sum_{c\in C}||\mu_c|| lreg?=∣C∣1?c∈C∑?∣∣μc?∣∣
其中的距离函数
φ
\varphi
φ设计为分段形式,公式如下:
φ
v
a
r
=
{
∣
∣
μ
c
?
h
i
∣
∣
?
δ
d
+
(
δ
d
?
δ
v
)
2
,
∣
∣
μ
c
?
h
i
∣
∣
>
δ
d
(
∣
∣
μ
c
?
h
i
∣
∣
?
δ
v
)
2
,
δ
d
>
∣
∣
μ
c
?
h
i
∣
∣
?
δ
v
0
∣
∣
μ
c
?
h
i
∣
∣
?
δ
d
\varphi_{var}=\left\{ \begin{array}{l} ||\mu_c-h_i||-\delta{_d}+(\delta{_d}-\delta{_v})^2,&||\mu_c-h_i||>\delta{_d}\\ (||\mu_c-h_i||-\delta{_v})^2,&\delta{_d}>||\mu_c-h_i||\geqslant\delta{_v}\\ 0 &||\mu_c-h_i||\leqslant\delta{_d} \end{array}\right.
φvar?=????∣∣μc??hi?∣∣?δd?+(δd??δv?)2,(∣∣μc??hi?∣∣?δv?)2,0?∣∣μc??hi?∣∣>δd?δd?>∣∣μc??hi?∣∣?δv?∣∣μc??hi?∣∣?δd??
φ d i s = { ( 2 δ d ? ∣ ∣ μ c a ? μ c b ∣ ∣ ) 2 , ∣ ∣ μ c a ? μ c b ∣ ∣ ? 2 δ d 0 , ∣ ∣ μ c a ? μ c b ∣ ∣ > 2 δ d \varphi_{dis}=\left\{\begin{array} {l} (2\delta{_d}-||\mu_{c_a}-\mu_{c_b}||)^2,&||\mu_{c_a}-\mu_{c_b}||\leqslant2\delta{_d}\\ 0,&||\mu_{c_a}-\mu_{c_b}||>2\delta{_d} \end{array}\right. φdis?={(2δd??∣∣μca???μcb??∣∣)2,0,?∣∣μca???μcb??∣∣?2δd?∣∣μca???μcb??∣∣>2δd??
本文中,距离阈值的设置为 δ v = 0.5 , δ d = 1.5 \delta{_v}=0.5,\delta{_d}=1.5 δv?=0.5,δd?=1.5
为了加速计算,对RCCA的输入进行降维,其比率设置为16
总的损失函数定义如下:
l
=
l
s
e
g
+
α
l
v
a
r
+
β
l
d
i
s
+
γ
l
r
e
g
l=l_{seg}+\alpha l_{var}+\beta l_{dis}+\gamma l_{reg}
l=lseg?+αlvar?+βldis?+γlreg?
本文中,
α
,
β
,
γ
\alpha,\beta,\gamma
α,β,γ??的值分别为1,1,0.001,
3D Criss-Cross Attention
在2D注意力的基础上进行推广,提出3DCCA,其可以在时间维度上收集额外的上下文信息
其流程与2DCCA大致相同,具体细节差异看论文。
代码复现
Criss-Cross Attention
def INF(B,H,W):
# tensor -> torch.size([H]) -> 对角矩阵[H,H] -> [B*W,H,H]
# 消除重复计算自身的影响
return -torch.diag(torch.tensor(float("inf")).cuda().repeat(H),0).unsqueeze(0).repeat(B*W,1,1)
class CrissCrossAttention(nn.Module):
""" Criss-Cross Attention Module"""
def __init__(self, in_ch,ratio=8):
super(CrissCrossAttention,self).__init__()
self.q = nn.Conv2d(in_ch, in_ch//ratio, 1)
self.k = nn.Conv2d(in_ch, in_ch//ratio, 1)
self.v = nn.Conv2d(in_ch, in_ch, 1)
self.softmax = nn.Softmax(ch=3)
self.INF = INF
self.gamma = nn.Parameter(torch.zeros(1)) # 初始化为0
def forward(self, x):
bs, _, h, w = x.size()
# Q
x_q = self.q(x)
# b,c',h,w -> b,w,c',h -> b*w,c',h -> b*w,h,c'
# 后两维相当于论文中的Q_u,在此分解为了
x_q_H = x_q.permute(0,3,1,2).contiguous().view(bs*w,-1,h).permute(0, 2, 1)
# b,c',h,w -> b,h,c',w -> b*h,c',w -> b*h,w,c'
x_q_W = x_q.permute(0,2,1,3).contiguous().view(bs*h,-1,w).permute(0, 2, 1)
# K
x_k = self.k(x) # b,c',h,w
# b,c',h,w -> b,w,c',h -> b*w,c',h
x_k_H = x_k.permute(0,3,1,2).contiguous().view(bs*w,-1,h)
# b,c',h,w -> b,h,c',w -> b*h,c',w
x_k_W = x_k.permute(0,2,1,3).contiguous().view(bs*h,-1,w)
# V
x_v = self.v(x)
# b,c,h,w -> b,w,c,h -> b*w,c,h
x_v_H = x_v.permute(0,3,1,2).contiguous().view(bs*w,-1,h)
# b,c,h,w -> b,h,c,w -> b*h,c,w
x_v_W = x_v.permute(0,2,1,3).contiguous().view(bs*h,-1,w)
# torch.bmm计算三维的矩阵乘法,如[bs,a,b][bs,b,c]
# 先计算所有Q_u和K上与位置u同一列的
energy_H = (torch.bmm(x_q_H, x_k_H)+self.INF(bs, h, w)).view(bs,w,h,h).permute(0,2,1,3) # b,h,w,h
# 再计算行
energy_W = torch.bmm(x_q_W, x_k_W).view(bs,h,w,w)
# 得到注意力图
concate = self.softmax(torch.cat([energy_H, energy_W], 3)) # b,h,w,h+w
# 后面开始合成一张图
att_H = concate[:,:,:,0:h].permute(0,2,1,3).contiguous().view(bs*w,h,h)
#print(concate)
#print(att_H)
att_W = concate[:,:,:,h:h+w].contiguous().view(bs*h,w,w)
# 同样的计算方法
out_H = torch.bmm(x_v_H, att_H.permute(0, 2, 1)).view(bs,w,-1,h).permute(0,2,3,1) # b,c,h,w
out_W = torch.bmm(x_v_W, att_W.permute(0, 2, 1)).view(bs,h,-1,w).permute(0,2,1,3) # b,c,h,w
#print(out_H.size(),out_W.size())
return self.gamma*(out_H + out_W) + x # 乘积使得整体可训练
Category Consistent Loss
未找到代码
实验
在Cityscapes、ADE20K、COCO、LIP和CamVid数据集上进行了实验,在一些数据集上实现了SOTA,并且在Cityscapes数据集上进行了消融实验。
实验结果
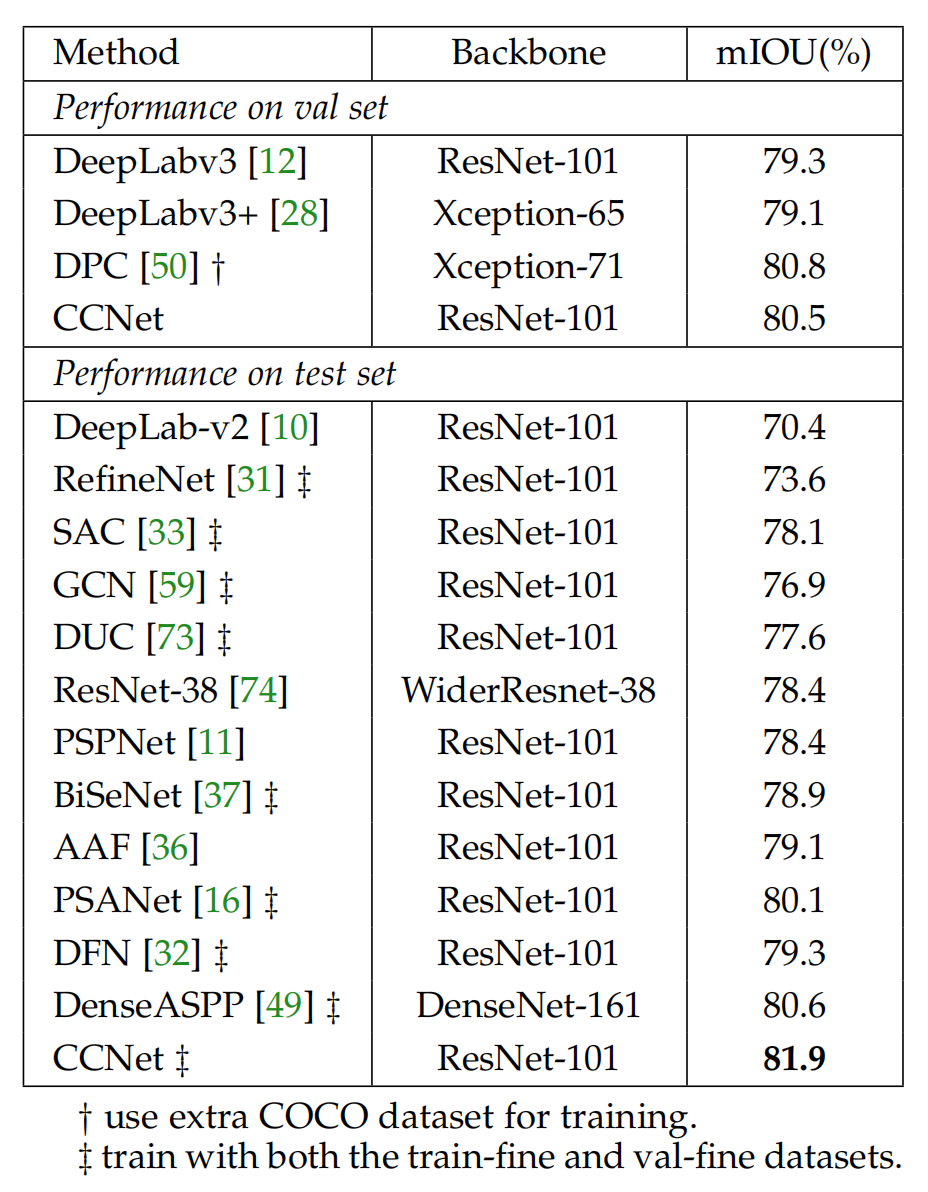
在Cityscapes上的结果:
消融实验
RCCA模块
通过改变循环次数进行了如下实验:
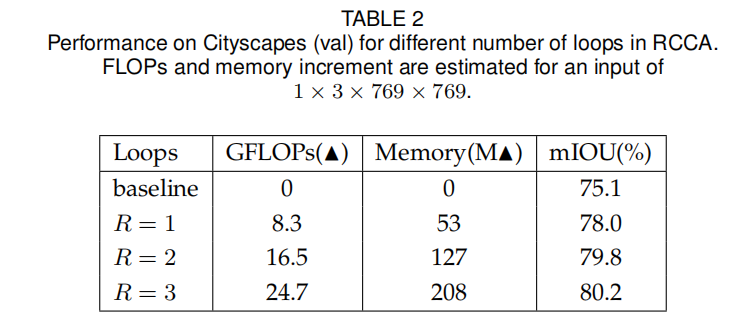
可以看到,RCCA模块可以有效的聚集全局上下文信息,同时保持较低的计算量。
为了进一步验证CCA的有效性,进行了定性比较:
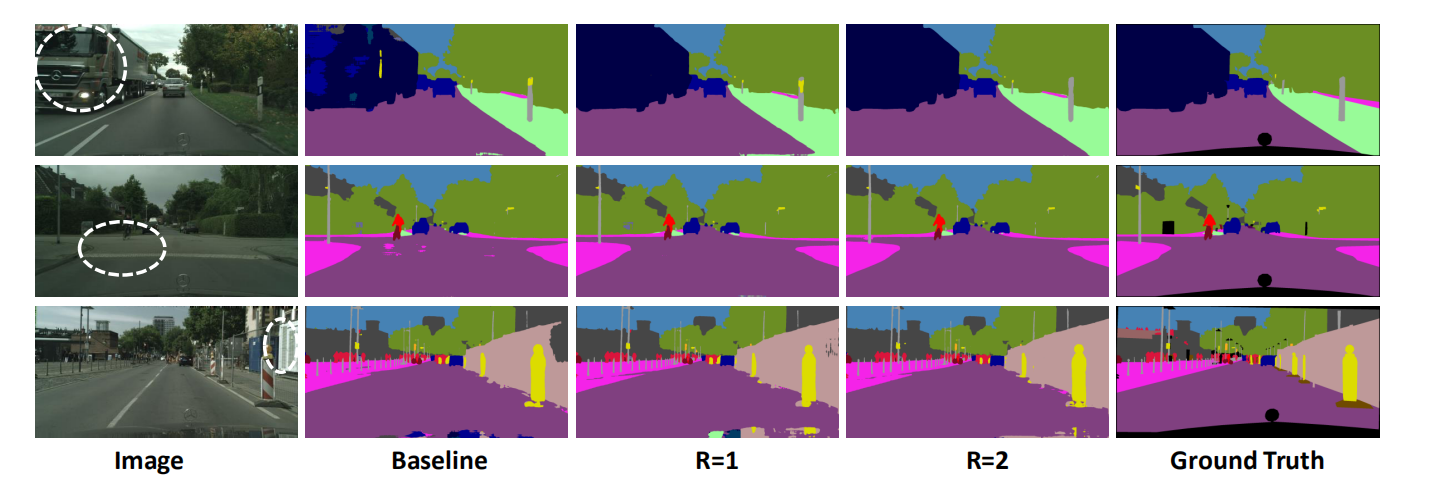
随着循环次数的增加,这些白色圈圈区域的预测逐渐得到纠正,这证明了密集上下文信息在语义分割中的有效性。
类别一致损失
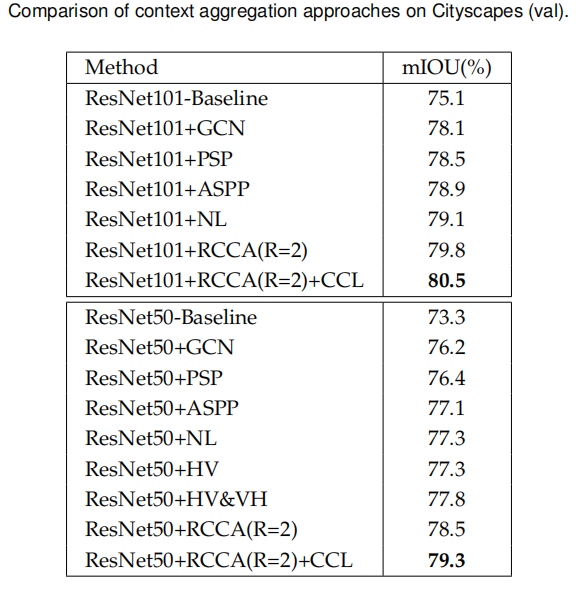
上图中的CCL即表示使用了类别一致损失
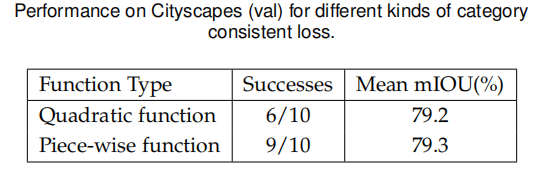
上述结果表明了分段距离和类别一致损失的有效性。
对比其他聚集上下文信息方法

同时,对Non Local使用了循环操作,可以看到,循环操作带来了超过一点的增益,然而其巨量的计算量和显存需求限制性能

可视化注意力图

上图中可以看到循环操作的有效性。
更多实验
在ADE20K上的实验验证了类别一致损失(CCL)的有效性:

在LIP数据集的实验结果:

在COCO数据集的实验结果:

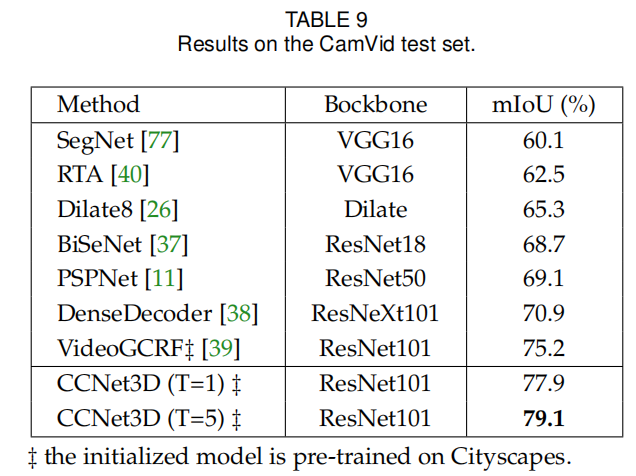
在CamVid数据上的实验结果: