[人工智能]《模式识别导论》第2章(聚类分析)学习笔记

第2章 聚类分析

2.1 距离聚类的概念

理解为什么使用距离进行聚类

能从给定的例子中找出可用于分类的距离

• 什么是聚类分析？
  • 根据模式样本之间的相似性对模式样本进行分类
• 聚类分析的前提条件
  • 样本所属类别未知
• 聚类分析的目标
  • 将相似的样本归为一类
  • 将不相似的样本归为不同类
• 聚类分析的例子
  • 将班上同学分类为男同学和女同学
• 什么是相似性？
  • 每个样本由多个特征组成X=[x1,x2,…,xn]
  • X可以看成是n维空间的一个点
  • 点之间的距离代表着样本的相似性
• 聚类分析的关键问题
  • 特征选择：略去多余的特征，选择合适的特征
  • 特征量化：连续量的量化、数量级标准化、特征权重、归一化

2.2.1 常用的距离

会使用各种距离公式计算样本间的距离

能指出各种距离的优缺点

• 欧氏距离（Euclid，欧几里德）用于计算任意两样本的距离

  • 输入：两个n维模式样本X1,X2
    $$\begin{gathered} X_1=[x_{11},x_{12},\dots ,x_{1n}{]}^T \\ {X}_2=[x_{21},x_{22},\dots ,x_{2n}{]}^T \end{gathered}$$

  • 计算公式：
    $$D(X_1,X_2)=||X_1?X_2||=\sqrt{(X_1?X_2{)}^T(X_1?X_2)}=\sqrt{(x_{11}?x_{21}{)}^2+?+(x_{1n}?x_{2n}{)}^2}$$

  • 输出(标量):
    $$D(X_1,X_2)=||X_1?X_2||$$

  • 要求：

    • 各维度上是相同的物理量
    • 各维度上的物理量单位相同

  • 问题：

    • 单位或物理量不同时会出现不同的聚类结果

  • 解决办法：

    • 标准化、归一化
      $$归一化公式：x^{\prime }=(x?x_{min})/(x_{max}?x_{min})$$

  • 优点：

    • 多个维度为同一个物理量且单位相同时，效果很好

  • 缺点：

    • 多个维度为不同物理量时，需要归一化
    • 多个维度为不同单位时，需要标准化

• 马氏距离（Maharanobis）用于计算样本偏离总体的程度

  • 输入：一个n维模式样本X，样本总体的均值向量M，样本总体的协方差矩阵C
    X = [ x 1 ? x n ] ???? M = [ m 1 ? m n ] C = E { ( X ? M ) ( ( X ? M ) ) T } = E { [ ( x 1 ? m 1 ) ( x 2 ? m 2 ) ? ( x n ? m n ) ] [ ( x 1 ? m 1 ) ( x 2 ? m 2 ) … ( x n ? m n ) ] } = [ E ( x 1 ? m 1 ) ( x 1 ? m 1 ) E ( x 1 ? m 1 ) ( x 2 ? m 2 ) ? E ( x 1 ? m 1 ) ( x n ? m n ) E ( x 2 ? m 2 ) ( x 1 ? m 1 ) E ( x 2 ? m 2 ) ( x 2 ? m 2 ) ? ? ? ? ? ? E ( x n ? m n ) ( x 1 ? m 1 ) ? ? E ( x n ? m n ) ( x n ? m n ) ] = [ σ 11 2 σ 12 2 ? σ 1 n 2 σ 21 2 ? σ j k 2 ? ? ? σ k k 2 ? σ n 1 2 ? ? σ n n 2 ] X=\begin{bmatrix} {x_1}\\ {\vdots}\\ {x_n}\\ \end{bmatrix}\ \ \ \ M=\begin{bmatrix} m_1\\ \vdots\\ m_n\\ \end{bmatrix}\\ C=E\{(X-M)((X-M))^T\}=E\{ \begin{bmatrix} {(x_1-m_1)}\\ {(x_2-m_2)}\\ \vdots\\ {(x_n-m_n)}\\ \end{bmatrix} [(x_1-m_1)(x_2-m_2)\dots(x_n-m_n)] \}\\ =\begin{bmatrix} {E(x_1-m_1)(x_1-m_1)}&{E(x_1-m_1)(x_2-m_2)}&{\cdots}&{E(x_1-m_1)(x_n-m_n)}\\ {E(x_2-m_2)(x_1-m_1)}&{E(x_2-m_2)(x_2-m_2)}&{\cdots}&{\cdots}\\ {\vdots}&{\vdots}&{\vdots}&{\vdots}\\ {E(x_n-m_n)(x_1-m_1)}&{\cdots}&{\cdots}&{E(x_n-m_n)(x_n-m_n)} \end{bmatrix}\\ =\begin{bmatrix} {\sigma_{11}^2}&{\sigma_{12}^2}&{\cdots}&{\sigma_{1n}^2}\\ {\sigma_{21}^2}&{\ddots}&{\sigma_{jk}^2}&{\vdots}\\ {\vdots}&{\vdots}&{\sigma_{kk}^2}&{\vdots}\\ {\sigma_{n1}^2}&{\cdots}&{\cdots}&{\sigma_{nn}^2}\\ \end{bmatrix} X=????x1??xn??????????M=????m1??mn??????C=E{(X?M)((X?M))T}=E{??????(x1??m1?)(x2??m2?)?(xn??mn?)???????[(x1??m1?)(x2??m2?)…(xn??mn?)]}=??????E(x1??m1?)(x1??m1?)E(x2??m2?)(x1??m1?)?E(xn??mn?)(x1??m1?)?E(x1??m1?)(x2??m2?)E(x2??m2?)(x2??m2?)????????E(x1??m1?)(xn??mn?)??E(xn??mn?)(xn??mn?)???????=???????σ112?σ212??σn12??σ122??????σjk2?σkk2???σ1n2???σnn2?????????

    1. E表示平均值，C计算公式中的X代表所有样本，而不是单个！！！
    2. C表示样本总体在各维上的分散情况，越大越分散

  • 计算公式：
    $$D^2=(X?M{)}^T{C}^{?1}(X?M)$$
    公式含义：某个样本点到均值向量的距离的平方，表示样本偏离总体模式类的程度。距离越大与该模式类越不相似

  • 输出(标量)：
    $$D^2$$

  • 马氏距离与欧氏距离之间的关系
    $$\begin{gathered} D(X_1,X_2)=||X_1?X_2||=\sqrt{(X_1?X_2{)}^T(X_1?X_2)} \\ {D}^2=(X?M{)}^T{C}^{?1}(X?M) \end{gathered}$$

    1. 马氏距离依赖于总体样本

    2. 当C=I时，马氏距离为欧氏距离

    3. 到均值向量的欧氏距离相等的点A和B在同一个圆上；

       到均值向量的马氏距离相等的点A和B依赖于样本的分布（C代表了分布）

  • 要求：

    • 各维度上可以是不同的物理量
    • 各维度上的物理量单位可以不同

  • 优点：

    • 可以消除量纲的影响
    • 可以排除多个维度特征之间的关联

  • 缺点：

    • 要求总体样本数量大于每个样本的维数，否则协方差矩阵不存在逆矩阵（一般能满足）

• 明氏距离（Minkowaki）用于计算任意两样本的距离

  • 输入：
    $$\begin{gathered} 两个n维模式样本X_i,X_j \\ {X}_i=[x_{i1},x_{i2},\dots ,x_{in}{]}^T \\ {X}_j=[x_{j1},x_{j2},\dots ,x_{jn}{]}^T \end{gathered}$$

  • 计算公式：
    $$D_m(X_i,X_j)=[\sum _{k=1}^n|x_{ik}?x_{jk}{|}^m{]}^{1/m}$$

  • 输出(标量)：
    $$D_m(X_i,X_j)$$

  • 公式含义：明氏距离是欧氏距离、曼哈顿距离、切比雪夫距离的推广与统一

    1. 当m=2时，明氏距离为欧氏距离

    2. 当m=1时，
       $$D_1(X_i,X_j)=\sum _{k=1}^n|x_{ik}?x_{jk}|$$
       称为“街坊”距离（又称为曼哈顿距离）

    3. 当m→∞时，明氏距离为切比雪夫距离
       $$D_{\infty }=max(|x_{ik}?x_{jk}|),k=1,2,...,n$$
       起最大作用的分量

  • 要求：

    • 各维度上是相同的物理量
    • 各维度上的物理量单位相同

  • 问题：

    • 单位或物理量不同时会出现不同的聚类结果

  • 解决办法：

    • 标准化、归一化

  • 优点：

    • 多个维度为同一个物理量且单位相同时，效果很好

  • 缺点：

    • 多个维度为不同物理量时，需要归一化
    • 多个维度为不同单位时，需要标准化

• 汉明距离（Hamming）用于计算任意两二值样本的距离

  • 输入：
    $$\begin{gathered} 两个n维二值（1或?1）模式样本X_i,X_j \\ {X}_i=[x_{i1},x_{i2},\dots ,x_{in}{]}^T \\ {X}_j=[x_{j1},x_{j2},\dots ,x_{jn}{]}^T \end{gathered}$$

  • 计算公式：
    $$D_h(X_i,X_j)=\frac{1}{2}(n?\sum _{k=1}^n{x}_{ik}?x_{jk})$$

  • 输出（标量）：
    $$\begin{gathered} D_h(X_i,X_j) \\ 两个模式向量的各分量取值均不同：D_h(X_i,X_j)=n; \\ 两个模式向量的各分量取值全相同：D_h(X_i,X_j)=0 \end{gathered}$$

  • 要求：

    • 各维度上是二值数据[1,-1]

  • 问题：

    • 不是二值数据
    • 不是1和-1

  • 解决办法：

    • 二值化、码型变换

  • 优点：

    • 能很好的反映两个二值样本的相似程度
    • 与单位无关
    • 与物理量无关

  • 缺点：

    • 维度数据不是二值时，需要二值化
    • 维度数据不是1和-1时，需要码型转换

• 角度相似性函数 用于计算任意两个样本的夹角

  • 输入：
    $$\begin{gathered} 两个n维模式样本X_i,X_j \\ {X}_i=[x_{i1},x_{i2},\dots ,x_{in}{]}^T \\ {X}_j=[x_{j1},x_{j2},\dots ,x_{jn}{]}^T \end{gathered}$$

  • 计算公式：
    $$S(X_i,X_j)=\frac{X_i^T{X}_j}{||X_i||?||X_j||}$$

  • 输出（标量）：
    $$S(X_i,X_j)$$

  • 要求：

    • 各维度上是相同的物理量
    • 各维度上的物理量单位相同

  • 问题：

    • 单位或物理量不同时会出现不同的聚类结果

  • 解决办法：

    • 标准化、归一化

  • 优点：

    • 多个维度为同一个物理量且单位相同时，效果很好
    • 具有旋转不变性（向量旋转）
    • 二值情况下与汉明距离有点相似，也是点积

  • 缺点：

    • 多个维度为不同物理量时，需要归一化
    • 多个维度为不同单位时，需要标准化

• 其它距离

  • 卡方距离：反映实际值与理论值的偏离程度
  • DTW距离：可用于比较两个长短不一的时间序列之间的相似度
  • 皮尔森相关系数：反映两个样本的相关性

• 距离公式汇总表

  	描述	单位	物理量
  欧氏	两个样本向量距离	同	同
  马氏	样本向量偏离中心的距离	不同	不同
  明氏	欧氏、街坊、曼氏、卡氏推广	同	同
  汉明	两个二值样本距离	无	无
  角度	两个样本向量夹角	同	同

2.2.2 聚类准则

理解聚类准则要解决的问题

会根据实际应用确定合适的阈值和聚类准则函数

• 聚类准则概念

  • 定义：根据相似性测度确定的，衡量模式之间是否相似的标准。即把不同模式聚为一类还是归为不同类的准则
  • 目标：样本间距离小到什么程度时，可归为一类？聚类准则确定
  • 聚类准则的确定方法：
    • 阈值准则：根据规定的距离阈值进行分类的准则
    • 函数准则：利用聚类准则函数进行分类的准则

• 聚类准则函数

  • 定义：在聚类分析中，表示模式类间相似或差异性的函数

  • 准则函数讨论：

    1. 它应是模式样本集{X}和模式类别{Sj, j=1,2,…,c}的函数

       着眼于整体，而不是个体

    2. 可使聚类分析转化为寻找准则函数极值的最优化问题

  • 聚类准则函数例子：误差平方和函数
    $$\begin{gathered} J=\sum _{j=1}^c\sum _{X\in S_j}||X?M_j|{|}^2 \\ 式中：c为聚类类别的数目，M_j=\frac{1}{N_j}\sum _{X\in S_j}X为属于S_j集的样本的均值向量， \\ {N}_j为S_j中样本数目 \end{gathered}$$

  • 适用范围：

    • 样本类数给定
    • 各类样本密集且相差不多，而不同类间的样本又明显分开的情况

• 误差平方和函数的例子1

  • **最好结果示例（a）：**类内误差平方和很小，类间距离很远

  

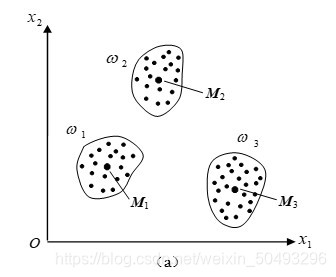
  • **不好结果示例（b）：**W1类长轴两端距离中心很远，J值较大

  

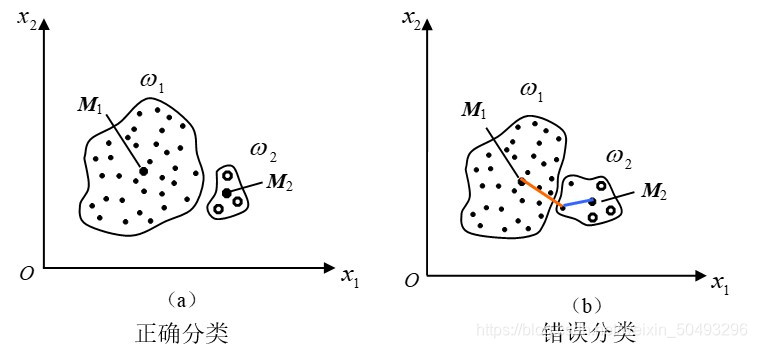
• 误差平方和函数的例子2

  有时可能把样本数目多的一类分拆为二，造成错误聚类

  原因：这样分开，J值会更小

  

2.3 基于距离阈值的聚类算法

会使用各种聚类算法进行聚类

能指出各种聚类算法的优缺点

• 基于距离阈值的聚类：近邻聚类法

  将样本按照距离阈值T分类到若干模式类中

  • 输入：
    N 个 待 分 类 的 模 式 样 本 { X 1 , X 2 , … , X N } N个待分类的模式样本\{X_1,X_2,\dots,X_N\} N个待分类的模式样本{X1?,X2?,…,XN?}

  • 输出：
    $$以Z_1,Z_2,\dots 为聚类中心的若干模式类$$

  • 算法描述：

    步骤1：
    $$任取样本X_i作为第一个聚类中心的初始值，如令Z_1=X_1$$
    步骤2：
    $$\begin{gathered} 计算样本X_2到Z_1的欧氏距离D_{21}=||X_2?Z_1||，若D_{21}>T,定义一新的聚类中心Z_2=X_2; \\ 否则X_2\in 以Z_1为中心的聚类 \end{gathered}$$
    步骤3：
    $$\begin{gathered} 假设已有聚类中心Z_1,Z_2,计算D_{31}=||X_3?Z_1||和D_{32}=||X_3?Z_2||， \\ 若D_{31}>T且D_{32}>T，则建立第三个聚类中心Z_3=X_3; \\ 否则X_3\in 离Z_1和Z_2中最近者（最近邻的聚类中心）。...... \\ 依此类推，直到将所有的N个样本都进行分类 \end{gathered}$$

  • 优点：

    • 计算简单、快速

  • 缺点：

    • 依赖于距离阈值T的大小
    • 依赖于第一个聚类中心的位置选择
    • 依赖于待分类模式样本的排列次序
    • 依赖于样本分布的几何性质

  • 图示：阈值T、中心Z、样本顺序的影响

    用先验知识指导阈值T和起始点Z1的选择，可获得合理的聚类结果。否则只能选择不同的初值重复试探，并对聚类结果进行验算，根据一定的评价标准，得出合理的聚类结果

    

• 基于距离阈值的聚类：最大最小距离算法

  将样本按照距离阈值T分类到若干模式类中

  • 输入：
    N 个 待 分 类 的 模 式 样 本 { X 1 , X 2 , … , X N } N个待分类的模式样本\{X_1,X_2,\dots,X_N\} N个待分类的模式样本{X1?,X2?,…,XN?}

  • 输出：
    $$以Z_1,Z_2,\dots 为聚类中心的若干模式类$$

  • 算法描述：

    步骤1：
    $$选任意一模式样本做为第一聚类中心Z_1$$
    步骤2：
    $$选择离Z_1距离最远的样本作为第二聚类中心Z_2$$
    步骤3：
    $$\begin{gathered} 逐个计算各模式样本与已确定的所有聚类中心之间的距离，并选出其中的最小距离。 \\ 例当聚类中心数k=2时，计算D_{i1}=||X_i?Z_1||和D_{i2}=||X_i?Z_2|| \\ min(D_{i1},D_{i2}),i=1,\dots ,N(N个最小距离) \end{gathered}$$
    步骤4：
    在 所 有 最 小 距 离 中 选 出 最 大 距 离 ， 如 该 最 大 值 达 到 ∣ ∣ Z 1 ? Z 2 ∣ ∣ 的 一 定 分 数 比 值 （ 阈 值 T ） 以 上 （ 即 T = θ ∣ Z 1 ? Z 2 ∣ ） , 则 相 应 的 样 本 点 取 为 新 的 聚 类 中 心 ， 返 回 步 骤 3 ； 否 则 聚 类 中 心 的 工 作 结 束 例 k = 2 时 ， 若 m a x { m i n ( D i 1 , D i 2 ) , i = 1 , 2 , … , N } > θ ∣ ∣ Z 1 ? Z 2 ∣ ∣ , 0 < θ < 1 则 Z 3 存 在 。 （ θ ： 用 试 探 法 取 为 一 固 定 分 数 ， 如 1 / 2 ） 在所有最小距离中选出最大距离，如该最大值达到||Z_1-Z_2||的一定分数比值（阈值T）以上\\ （即T=\theta|Z_1-Z_2|）,则相应的样本点取为新的聚类中心，返回步骤3；\\ 否则聚类中心的工作结束\\ 例k=2时，\\ 若max\{min(D_{i1},D_{i2}),i=1,2,\dots,N\}>\theta||Z_1-Z_2||,0<\theta<1\\ 则Z_3存在。（\theta：用试探法取为一固定分数，如1/2） 在所有最小距离中选出最大距离，如该最大值达到∣∣Z1??Z2?∣∣的一定分数比值（阈值T）以上（即T=θ∣Z1??Z2?∣）,则相应的样本点取为新的聚类中心，返回步骤3；否则聚类中心的工作结束例k=2时，若max{min(Di1?,Di2?),i=1,2,…,N}>θ∣∣Z1??Z2?∣∣,0<θ<1则Z3?存在。（θ：用试探法取为一固定分数，如1/2）
    步骤5：

    重复步骤3、4，直到没有新的聚类中心出现为止

    步骤6：
    将 样 本 { X i , i = 1 , 2 , … , N } 按 最 近 距 离 划 分 到 相 应 聚 类 中 心 对 应 的 类 别 中 将样本\{X_i,i=1,2,\dots,N\}按最近距离划分到相应聚类中心对应的类别中 将样本{Xi?,i=1,2,…,N}按最近距离划分到相应聚类中心对应的类别中
    思路总结：*

    先找出两个初始类（步骤1、2）；

    再确定更多的聚类中心（步骤3、4、5）；

    最后分类（步骤6）

    关键：确定聚类中心（步骤3、4、5）

  • 优点：

    • 计算简单、快速（比近邻聚类慢些）
    • 不依赖于待分类模式样本的排列次序

  • 缺点：

    • 依赖于距离阈值T的大小
    • 依赖于第一个聚类中心的位置选择
    • 依赖于样本分布的几何性质

• 基于距离阈值的聚类汇总

  	基于距离阈值	计算速度	依赖于阈值T	依赖于第一聚类中心	依赖于样本排列次序	依赖于几何分布
  近邻聚类	是	快	是	是	是	是
  最大最小距离聚类	是	较快	是	是	否	是

2.4 层次聚类法

按照距离准则逐步合并，减少类别数

又称（系统聚类法、分级聚类法）

• 输入：N个待分类的模式样本，各自为一类
  $$G_1(0),G_2(0),\dots ,G_N(0)$$

• 算法描述：

  步骤1：

  计算各样本间距离，得N×N维距离矩阵D(0)。“0”表示初始状态

  步骤2：
  $$\begin{gathered} 假设已求得距离矩阵D(n)(n为逐次聚类合并的次数)，找出D(n)中的最小元素，将其对应的两类合并为一类。 \\ 得新分类：G_1(n+1),G_2(n+1),\dots \end{gathered}$$
  步骤3：

  计算合并后新类之间的距离，得D(n+1)

  步骤4：

  跳至步骤2，重复计算及合并

• 输出：

  1. 取距离阈值T，当D(n)的最小分量超过给定值T时，算法停止。所得即为聚类结果
  2. 或不设阈值T，一直将全部样本聚成一类为止，输出聚类的分级树

• 类间距计算方法

  • 最短距离法

    使用最短距离作为类间距离

    • 输入：两个聚类H、K

    • 输出（标量）：最短距离

    • 计算公式：
      D H K = m i n { D ( X H , X K ) } ???? X H ∈ H , X K ∈ K D ( X H , X K ) ： H 类 中 样 本 X H 和 K 类 中 样 本 X K 之 间 的 欧 氏 距 离 D H K ： H 类 中 所 有 样 本 与 K 类 中 所 有 样 本 之 间 的 最 小 距 离 D_{HK}=min\{D(X_H,X_K)\}\ \ \ \ X_H\in H,X_K\in K\\ D(X_H,X_K)：H类中样本X_H和K类中样本X_K之间的欧氏距离\\ D_{HK}：H类中所有样本与K类中所有样本之间的最小距离 DHK?=min{D(XH?,XK?)}????XH?∈H,XK?∈KD(XH?,XK?)：H类中样本XH?和K类中样本XK?之间的欧氏距离DHK?：H类中所有样本与K类中所有样本之间的最小距离
      

    • 简化计算：

      如果K类由 I 和 J 两类合并而成，则，因为
      D H I = m i n { D ( X H , X I ) } ???? X H ∈ H , X I ∈ I D H J = m i n { D ( X H , X J ) } ???? X H ∈ H , X J ∈ J 所 以 ： D H K = m i n { D H I , D H J } D_{HI}=min\{D(X_H,X_I)\}\ \ \ \ X_H\in H,X_I\in I\\ D_{HJ}=min\{D(X_H,X_J)\}\ \ \ \ X_H\in H,X_J\in J\\ 所以：D_{HK}=min\{D_{HI},D_{HJ}\} DHI?=min{D(XH?,XI?)}????XH?∈H,XI?∈IDHJ?=min{D(XH?,XJ?)}????XH?∈H,XJ?∈J所以：DHK?=min{DHI?,DHJ?}
      

    • 优点：

      • 计算简单、快速

    • 缺点：

      • 易受个别异常点影响

  • 最长距离法

    使用最长距离作为类间距离

    • 输入：两个聚类H、K

    • 输出（标量）：最长距离

    • 计算公式：
      D H K = m a x { D ( X H , X K ) } ???? X H ∈ H , X K ∈ K D_{HK}=max\{D(X_H,X_K)\}\ \ \ \ X_H\in H,X_K\in K DHK?=max{D(XH?,XK?)}????XH?∈H,XK?∈K

    • 简化计算：若K类由 I , J 两类合并而成，则，因为
      D H I = m a x { D ( X H , X I ) } ???? X H ∈ H , X I ∈ I D H J = m a x { D ( X H , X J ) } ???? X H ∈ H , X J ∈ J D_{HI}=max\{D(X_H,X_I)\}\ \ \ \ X_H\in H,X_I\in I\\ D_{HJ}=max\{D(X_H,X_J)\}\ \ \ \ X_H\in H,X_J\in J\\ DHI?=max{D(XH?,XI?)}????XH?∈H,XI?∈IDHJ?=max{D(XH?,XJ?)}????XH?∈H,XJ?∈J
      所以： D H K = m a x { D H I , D H J } D_{HK}=max\{D_{HI},D_{HJ}\} DHK?=max{DHI?,DHJ?}

    • 优点：

      • 计算简单、快速

    • 缺点：

      • 易受个别异常点影响

  • 中间距离法

    使用中间距离作为类间距离

    • 输入：两个聚类H、K，其中类K由类 I 和 J 组成

    • 输出（标量）：中间距离

    • 计算公式：
      $$D_{HK}=\sqrt{D_{HI}^2/2+D_{HJ}^2/2?D_{IJ}^2/4}$$
      如果类 K 是单个元素，则按照最长或最短距离法计算

    • 优点：

      • 可降低个别异常点的影响

    • 缺点：

      • 计算复杂

  • 重心法

    使用重心距离作为类间距离

    • 输入：两个聚类H、K，其中若 I 类中有 $n_I$ 个样本，J 类中有 $n_J$ 个样本

    • 输出（标量）：重心距离

    • 计算公式：
      $$D_{HK}=\sqrt{\frac{n_I}{n_I+n_J}{D}_{HI}^2+\frac{n_J}{n_I+n_J}{D}_{HJ}^2?\frac{n_I{n}_J}{(n_I+n_J{)}^2}{D}_{IJ}^2}$$
      如果类 K 是单个元素，则按照最长或最短距离法计算

    • 重心法与中间距离法区别

      • 用样本数作为权重系数，而不是固定系数
      • 好处：大类权重大，从而避免了小类的个别样本占权重太大

    • 优点：

      • 可以降低少数异常点的影响

    • 缺点：

      • 计算复杂

  • 类平均距离法

    使用重心距离作为类间距离

    • 输入：两个聚类H、K

    • 输出（标量）：类平均距离

    • 计算公式：
      $$D_{HK}=\sqrt{\frac{1}{n_H{n}_K}\sum _{i\in Hj\in K}{d}_{ij}^2}$$
      $d_{ij}^2$ ：H类任一样本 $X_i$ 和 K 类任一样本 $X_j$ 之间的欧氏距离平方

      $n_H$ ：H 类的样本数量；

      $n_K$ ：K 类的样本数量

    • 简化计算：若 K 类由 I 类和 J 类合并产生，则递推式为
      $$D_{HK}=\sqrt{\frac{n_I}{n_I+n_J}{D}_{HI}^2+\frac{n_J}{n_I+n_J}{D}_{HJ}^2}$$

  • 距离计算公式汇总

    	公式	优点	缺点
    最短距离法	D H K = m i n { D ( X H , X K ) } ???? X H ∈ H , X K ∈ K D_{HK}=min\{D(X_H,X_K)\}\ \ \ \ X_H\in H,X_K\in K DHK?=min{D(XH?,XK?)}????XH?∈H,XK?∈K	计算简单	对异常点敏感
    最长距离法	D H K = m a x { D ( X H , X K ) } ???? X H ∈ H , X K ∈ K D_{HK}=max\{D(X_H,X_K)\}\ \ \ \ X_H\in H,X_K\in K DHK?=max{D(XH?,XK?)}????XH?∈H,XK?∈K	计算简单	对异常点敏感
    中间距离法	$D_{HK}=\sqrt{D_{HI}^2/2+D_{HJ}^2/2?D_{IJ}^2/4}$	能降低异常点的影响	计算复杂
    重心法	$D_{HK}=\sqrt{\frac{n_I}{n_I+n_J}{D}_{HI}^2+\frac{n_J}{n_I+n_J}{D}_{HJ}^2?\frac{n_I{n}_J}{(n_I+n_J{)}^2}{D}_{IJ}^2}$	能降低异常点的影响	计算复杂
    类平均距离法	$D_{HK}=\sqrt{\frac{1}{n_H{n}_K}{\sum }_{i\in Hj\in K}{d}_{ij}^2}$	能降低异常点的影响	计算复杂

2.5 动态聚类法

• 基本思路：

  

• 主要算法：

  • K-均值算法（或C-均值算法）
  • 迭代自组织的数据分析算法（ISODATA）

2.5.1 K-均值算法

• 条件及约定：

  • 设待分类的模式特征矢量集为 { x 1 , x 2 , … , x N } \{x_1,x_2,\dots,x_N\} {x1?,x2?,…,xN?}
  • 类的数目 K 是事先取定的

• 基本思想：

  • 首先任意选取 K 个聚类中心，按最小距离原则将各模式分配到 K 类的某一类
  • 动态调整聚类中心和各模式的类别，最终使准则函数取极小值

• 准则函数：聚类集中每一样本点到该类中心的距离平方和

• 准则函数数学公式：

  1. 单个聚类集准则函数：

     对于第 j 个聚类集，准则函数定义为
     $$\begin{gathered} J_i=\sum _{i=1}^{N_j}||X_i?Z_j|{|}^2,X_i\in S_j \\ {S}_j:第j个聚类集（域），聚类中心为Z_j \\ {N}_j:第j个聚类集S_j中所包含的样本个数 \end{gathered}$$

  2. 总体准则函数：

     对所有 K 个模式类有
     $$J=\sum _{j=1}^K\sum _{i=1}^{N_j}||X_i?Z_j|{|}^2,X_i\in S_j$$

• 聚类准则：聚类中心的选择应使准则函数 J 极小，即使 $J_j$ 的值极小

  对于某一个聚类 j ，应有 $\frac{?J_j}{?Z_j}=0$

  即 $\frac{?}{?Z_j}{\sum }_{i=1}^{N_j}||X_i?Z_j|{|}^2=\frac{?}{?Z_j}{\sum }_{i=1}^{N_j}(X_i?Z_j{)}^T(X_i?Z_j)=0$

  可解得 $Z_j=\frac{1}{N_j}{\sum }_{i=1}^{N_j}{X}_i,X_i\in S_j$

  上式表明，$S_j$ 类的聚类中心应选为该类样本的均值

• 算法描述：

  • 步骤1：确定初始聚类中心

    任选 K 个模式特征矢量作为初始聚类中心：

    $z_1(1),z_2(1),\dots ,z_k(1)$。其中括号内的序号表示迭代次数

  • 步骤2：根据聚类中心分类

    将待分类的样本集按最小距离原则分划给 K 类中的某一类：

    如果 D j ( k ) = m i n { ∣ ∣ x ? z i ( k ) ∣ ∣ } ?? ( i = 1 , 2 , … , K ) D_j(k)=min\{||x-z_i(k)||\} \ \ (i=1,2,\dots,K) Dj?(k)=min{∣∣x?zi?(k)∣∣}??(i=1,2,…,K)，则 $x\in S_j(k)$

  • 步骤3：确定新的聚类中心

    以各类的均值向量为新的聚类中心 $z_j(k+1)$，即：
    $$z_j(k+1)=\frac{1}{N_j}\sum _{x\in S_j(k)}x,j=1,2,\dots ,K$$

  • 步骤4：结束条件

    如果 $z_j(k+1)=z_j(k)(j=1,2,\dots ,K)$，则结束；否则，k=k+1，转（2）

• 优点：

  • 算法简单高效

• 缺点：

  • 结果受初始聚类中心位置影响
  • 结果受聚类中心个数影响
  • 结果受模式样本几何性质影响
  • 结果受样本顺序影响

• 解决办法：

  • 试探不同的 K 值
  • 选择不同的初始聚类中心

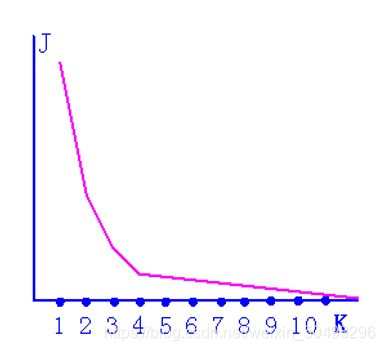
• 如何试探 K 值？

  根据聚类准则函数特点（下图）

  

• 准则函数特点：

  • 准则函数 J 随 K 值增大而减小
  • 准则函数到达合理 K 值前会急剧下降
  • 准则函数到达合理 K 值后会平缓下降

• 试探 K 值的方法：

  逐步增加 K 值试探

• 如何避免初始聚类中心数的影响？只有笨办法：多试试

  • 多次运行 K 均值算法，例如50~1000次，每次随机选取不同的初始聚类中心
  • 聚类结束后计算准则函数值
  • 选取准则函数值最小的聚类结果为最后的结果
  • 该方法一般适用于聚类数目小于10的情况

2.5.2 ISODATA

• K-均值算法的问题

  • 类别数 K 不能改变
  • 结果受初始聚类中心影响

• ISODATA 算法的改进

  • 动态改变类别数目

    • 通过类别的合并与分裂来实现

  • 合并

    • 如下两种情况合并：
      1. 类内样本个数太少
      2. 两聚类中心之间距离太小

  • 分裂

    • 如下情况分裂：

      某一类的类内方差过大时，宜分裂成两类，以维持合理的类内方差

• 基本步骤和思路

  1. 初始化

     选择初始控制参数和聚类中心

  2. 分类

     按照最近邻（即最短距离）规则进行分类

  3. 分裂与合并

     根据参数分裂和合并，并获得新聚类中心

  4. 结果评估

     评估结果是否符合要求。不符则返回（2）

• 初始化（第一步）

  设置控制参数、聚类数和初始聚类中心（见下表）

  参数	描述
  $K$	希望的聚类中心数目
  ${\theta }_N$	每个聚类中最少的样本数。用于控制合并
  ${\theta }_C$	两聚类中心间的最短距离。用于控制合并
  ${\theta }_S$	标准差阈值。所有分量中的最大值应小于 ${\theta }_s$，否则分裂
  $L$	每次迭代允许合并的最大聚类对数
  $N_c$	初始聚类数（可不等于 K ）
  $z_i,i=1,2,\dots ,N_c$	预设的初始聚类中心（也可在样本中选择）
  $I$	允许迭代的最大次数

• 分类（第二步）

  按最小距离聚类
  $$\begin{gathered} 若D_j=min(||x?z_i||),i=1,2,\dots ,N_c, \\ 则x\in S_j \end{gathered}$$

• 初步合并（第三步）

  若有任何一个类 $S_j$ ，其样本数 $N_j<{\theta }_N$，则舍去 $S_j$，令 $N_c=N_c?1$，将原样本分配至其它类

• 合并/分裂预处理（第四、五、六步）

  • 修正各聚类中心值（第四步）
    $$Z_j=\frac{1}{N_j}\sum _{X\in S_j}X，j=1,2,\dots ,N_c$$

  • 计算类内平均距离（第五步）
    $$D_j=\frac{1}{N_j}\sum _{x\in S_j}||x?z_j||,j=1,2,\dots ,N_c$$

  • 计算全体样本平均距离（第六步）
    $$D=\frac{1}{N}\sum _{j=1}^{N_c}{N}_j{D}_j$$

• 合并/分裂判决（第七步）

  • 如这是最后一次迭代（取决于 I ）,则不再合并分裂，转第十一步，善后处理；并设置 ${\theta }_c=0$ ，防止合并发生
  • 如果 $N_c\le K/2$ （类数远小于期望值），则转向第八步，分裂；
  • 如果此时迭代运算次数是偶数次，或 $N_c\ge 2K$ ，则转至第十一步，合并；否则转至第八步，分裂
  • 基本判断步骤：
    • 先判断是否要结束
    • 再根据期望中心数判断分裂或合并

• 分裂（第八、九、十步）

  • 计算类内标准差向量（第八步）。对每个聚类 j ，求其标准差向量
    $$\begin{gathered} {\sigma }_j={\left(\begin{array}{cccc}{\sigma }_{j1}& {\sigma }_{j2}& ?& {\sigma }_{jn}\end{array}\right)}^t \\ {\sigma }_{ji}=\sqrt{\frac{1}{N_j}\sum _{y_k\in S_j}(y_{ki}?z_{ji}{)}^2} \end{gathered}$$
    其中，

    ${\sigma }_{ji}$ 是第 j 个聚类第 i 个分量的标准差，

    $y_{ki}$ 是第 j 类中第 k 个样本的第 i 分量，

    $z_{ji}$ 是均值向量 $z_j$ 的第 i 个分量，

    n 是样本特征维数，

    $j=1,2,\dots ,N_c$ 是聚类数，

    $i=1,2,\dots ,n$ 是维数

  • 计算每个类的标准差向量最大分量（第九步）
    $${\sigma }_{jmax},j=1,2,\dots ,c$$

  • 执行分裂（第十步）

    若任一个 ${\sigma }_{jmax},j=1,2,\dots ,c$ 有 ${\sigma }_{jmax}>{\theta }_s$ ，并且有

    （a）$D_j>D$ 且 $N_j>2{\theta }_N+1$

    或有

    （b）$N_c\le K/2$

    则把 $S_j$ 分裂成两个聚类，其中心相应为 $z_j^{+}$ 与 $z_j^{?}$，把原来的 $S_j$ 取消，且令 $N_c=N_c+1$。

    转第二步进行下一轮。

    其中 $z_j^{+}$ 与 $z_j^{?}$ 计算方法如下：

    给定一 k 值，0<k<1，令 $r_j=k{\sigma }_{jmax}$；$z_j^{+}=z_j+r_j$，$z_j^{?}=z_j?r_j$；

    其中 k 值应使 $S_j$ 中的样本到 $z_j^{+}$ 与 $z_j^{?}$ 的距离不同，但又应使 $S_j$ 中的样本仍然在分裂后的新样本类中

• 合并（第十一、十二、十三步）

  • 计算类间聚类中心距离（第十一步）

    i 类与 j 类的类间距离为
    $$D_{ij}=||z_i?z_j||,i=1,2,\dots ,N_c?1,j=i+1,i+2,\dots ,N_c$$

  • 列出类间距离过近者（第十二步）

    比较 $D_{ij}$ 与 ${\theta }_c$ 并将小于 ${\theta }_c$ 的按上升次序排列如下（该队列最大个数是控制合并对数的参数L）
    $$D_{i1j1}<D_{i2j2}<?<D_{iljl},l\le L$$

  • 执行合并（第十三步）

    从类间距离最小的两类开始执行合并过程，此时需将 $z_{kl}$ 与 $z_{jl}$ 合并，同时执行 $N_c=N_c?1$ 。

    新中心的计算公式如下：
    $$z_l=\frac{1}{N_{il}+N_{jl}}[N_{il}{z}_{il}+N_{jl}{z}_{jl}]$$

• 结束（第十四步）

  • 如是最后一次迭代则终止
  • 否则可根据需要转第一步或第二步（转第一步是为了更改控制数），同时迭代计数加 1

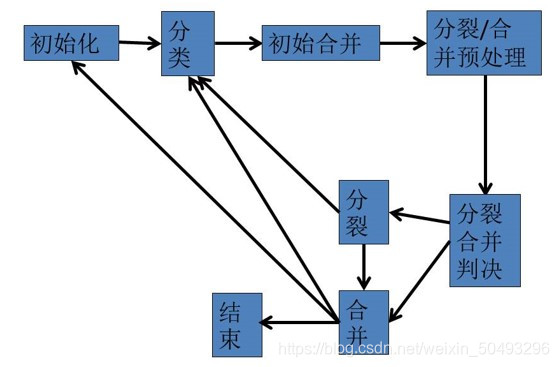
• 算法流程图

  

• 优点：

  • 聚类中心个数可调
  • 初始聚类中心位置对结果影响较小

• 缺点：

  • 结果受模式样本几何性质影响
  • 算法复杂

• ISODATA 与 K-均值算法比较

  	K-均值算法	ISODATA算法
  聚类中心通过样本均值迭代运算决定	是	是
  聚类中心数可变	否	是
  结果受初始聚类中心影响	是	否
  算法复杂度	简单	复杂
  结果受模式样本几何性质影响	是	是