一.引言
通过最基础的 DeepWalk 已经可以获取关注关系图中节点的 embedding,除了通过 embedding 计算内积获取两个节点的语义是否相近之外,还可以通过可视化的方式观测得到的 embedding。下面通过几种基本的降维方法获取降维后的向量与其对应的分布图,可以更好的分析和评估 embedding 质量。
Tips:

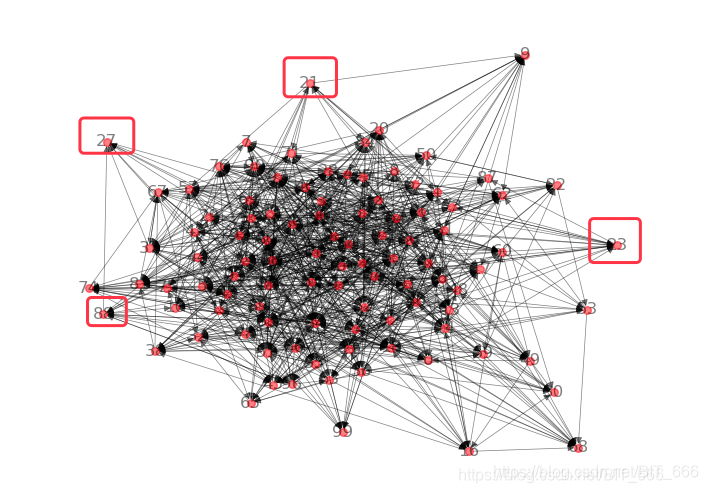
要降维的向量可以使用自己提前准备好的高维向量,也可以结合上一节?DeepWalk?生成的随机向量进行测试。上图为 DeepWalk 随机游走用到的图,其中节点数字标识该ID。
二.PCA
1.PCA 原理
PCA 主成分分析是最常见的降维方法,用于高维数据降维,可以提取数据的主要特征分量。实际操作过程中,主要通过计算协方差矩阵的特征值,将特征值按从高到低排序,根据降维选择的 dim=n,取前n个高的特征值对应的特征向量构成投影矩阵,从而将原始数据通过投影到低维(理论推导过程可以参考西瓜书)。结合现实场景,主成分分析就是希望降维后我们可以更多的获取多维数据的信息,以下面三维图三个视角为例:
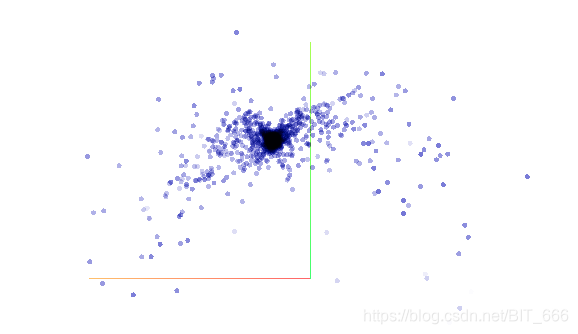
正面:
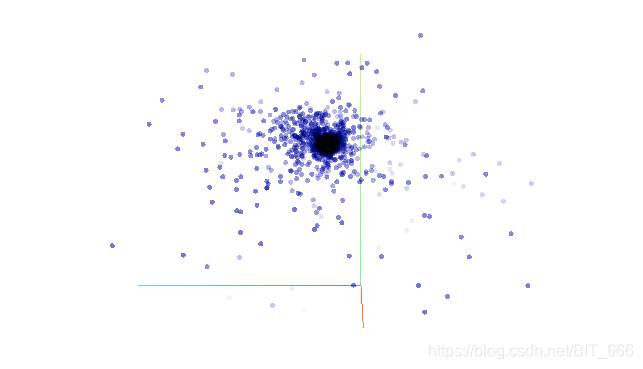
侧面:?
45度:?
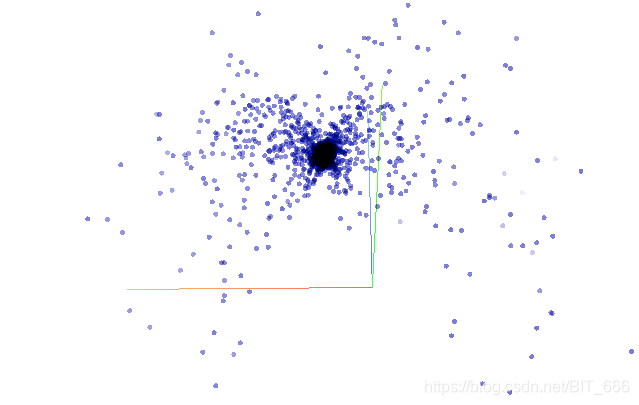
三张图可以理解为3维图像被降维至2维,前面和侧面相比45角都或多或少损失了一些图像的全貌,所以如果使用主成分分析,第一个特征值对应的特征向量肯定更偏向于在45度这张图附近生成,因为这里能够尽可能多的还原真实的图像原貌。
2.PCA实现
这里直接调用 python 库实现:
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
# Word2vec 得到的 id->embedding 的映射
embeddings = get_embeddings(model, G)
# 初始化 PCA 降维模型
pca = PCA(n_components=2)
embedding_list = [embeddings[k] for k in embeddings]
# 训练模型
compress_embedding = pca.fit_transform(embedding_list)
# 可视化
plt.scatter(compress_embedding[:, 0], compress_embedding[:, 1], s=10)
plt.title("Dim=2")
plt.colorbar()
plt.show()
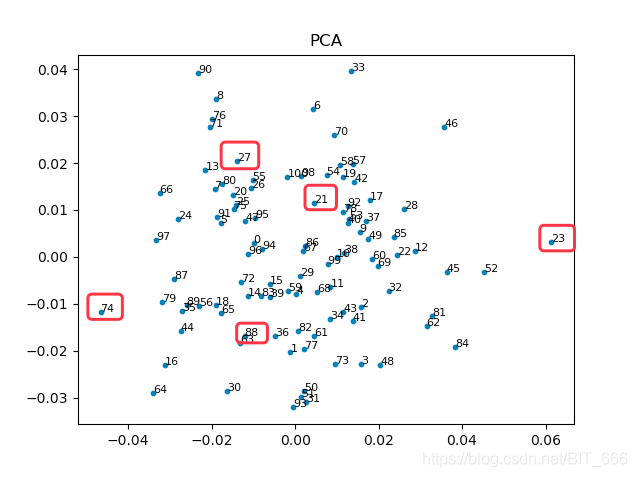
我们可以把原始的图看作是3维的用户关注关系,PCA(n_components=2) 看作是我们从某个视角观测且想要尽可能多的观测到的二维最全面的节点全貌,可以通过图中标识出的顶点去大致抽象一下这个降维过程。
三.TSNE
1.TSNE 原理
SNE - stochastic neighbor embedding 字面意思为随机领域嵌入,其核心思想是将图中的节点抽象为几何分布 P,将降维后的节点抽象为几何分布 Q,通过刻画两个分布的距离使二者距离达到最小,则认为降维损失了最少的原始信息,分布的距离通常使用 KL 散度定义,在 SNE 中,这个抽象的分布为高斯分布,这也是聚类,降维中常用到的分布函数,T-SNE 就是在 SNE 的基础上将高斯分布替换为 t 分布,其原因是 t 分布在低维空间下,同类数据距离较小,不同类数据距离较大,可视化效果更好,相关的 SNE, T-SNE 证明网上也有很多,感兴趣可以搜索一下 🔍
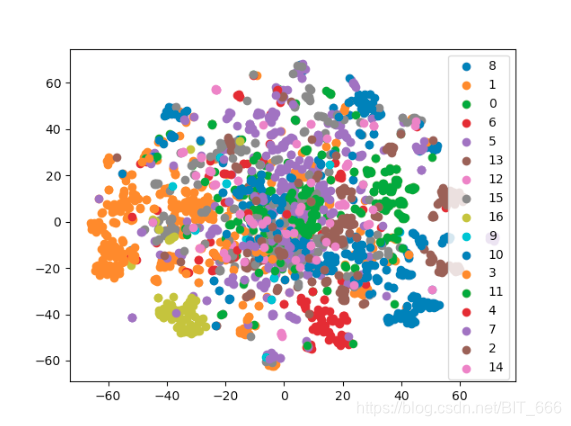
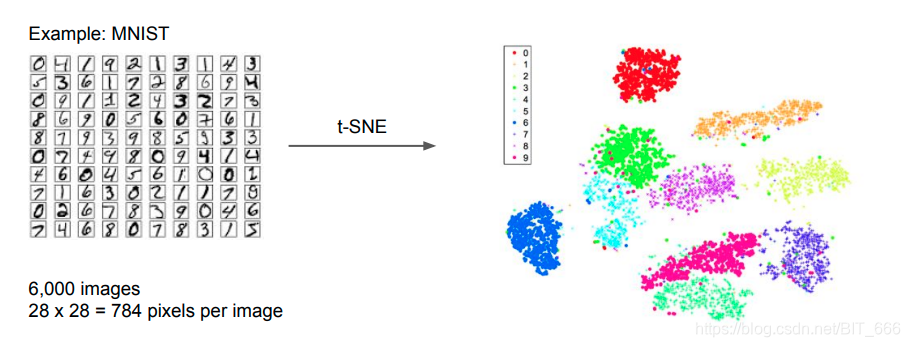
以手写数字数据为例,可以看到 T-SNE 的分类效果对于单类别特征更佳局促,可视化效果更好,体现了其在刻画局部特征的特点。

2.TSNE 实现
T-SNE 也直接调用 python 实现:
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
embeddings = get_embeddings(model, G)
embedding_list = [embeddings[k] for k in embeddings]
model = TSNE(n_components=2)
compress_embedding = model.fit_transform(embedding_list)
keys = list(embeddings.keys())
plt.scatter(compress_embedding[:, 0], compress_embedding[:, 1], s=10)
for x, y, key in zip(compress_embedding[:, 0], compress_embedding[:, 1], keys):
plt.text(x, y, key, ha='left', rotation=0, c='black', fontsize=8)
plt.title("T-SNE")
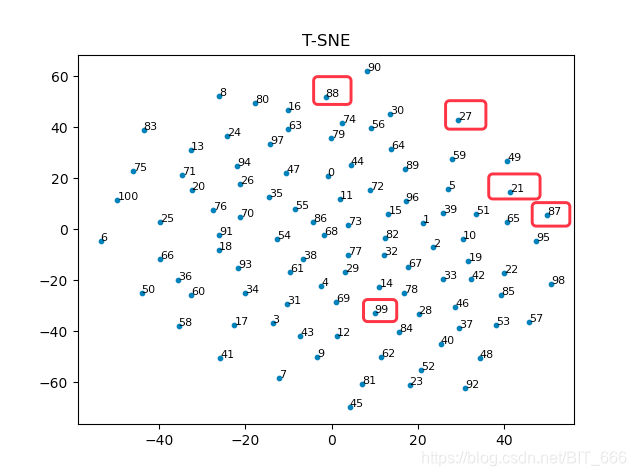
plt.show()可以看到,PCA 基于协方差矩阵和 T-SNE 基于分布距离对降维点选择的不同,PCA 更聚焦于通过更少的维度去描述高维图形,而 T-SNE 在则在点的分布以及点的稀疏程度与 PCA 形成不同对比。

四.AutoEncoder
1.AutoEncoder 原理
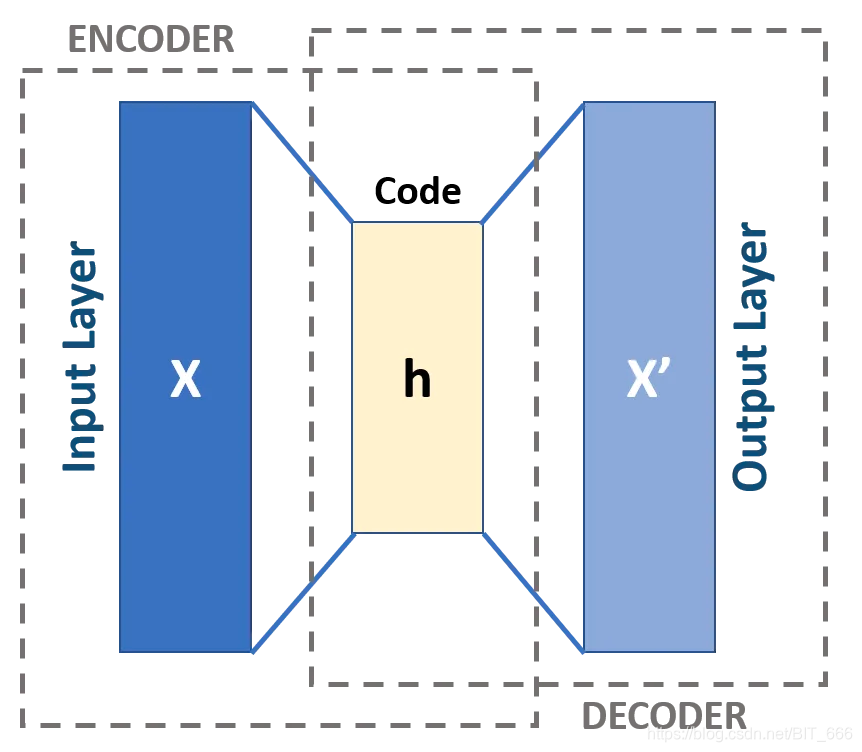
除了 PCA 和 T-SNE 外,对于无监督的聚类而言,深度学习中常用的就是 AutoEncoder 自编码器,通过 Encoder 和 Decoder 对向量本身学习进行信息整合,从低维度将高维度的数据恢复。最终训练结束保留 Encoder 作为降维使用,AutoEncoder 的实现与2D,3D可视化在之前的文章中提过,有兴趣可以参考。
?2.AutoEncoder 实现
from tensorflow.keras.models import Model # 泛型模型
import matplotlib.pyplot as plt
# 压缩特征维度至2维
encoding_dim = 2
input_emb = Input(shape=(emb_size,))
# 编码层
encoded = Dense(64, activation='relu')(input_emb)
encoded = Dense(10, activation='relu')(encoded)
encoder_output = Dense(encoding_dim)(encoded)
# 解码层
decoded = Dense(10, activation='relu')(encoder_output)
decoded = Dense(64, activation='relu')(decoded)
# 构建自编码模型
autoencoder = Model(inputs=input_emb, outputs=decoded)
# 构建编码模型
encoder = Model(inputs=input_emb, outputs=encoder_output)
# 编译模型
autoencoder.compile(optimizer='rmsprop', loss='mse')
# 训练模型
autoencoder.fit(embeddings, embeddings, epochs=20, batch_size=256, shuffle=True)
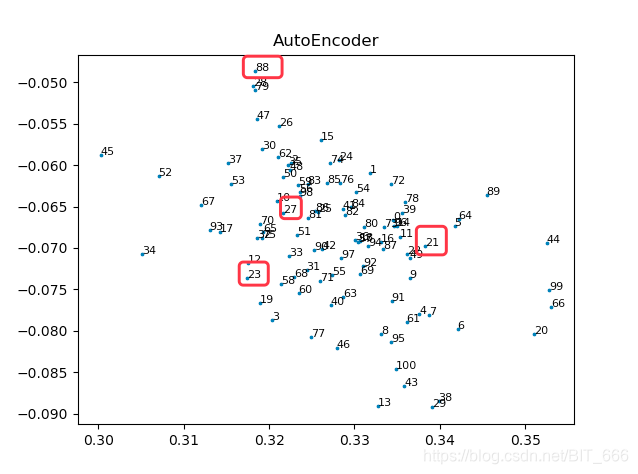
encoded_imgs = encoder.predict(embeddings)?AutoEncoder 相对于前两者都比较紧凑,相比于 PCA,因为隐层具有非线性变换单元,因此训练过程中可以挖掘更多潜在信息,但是缺点是如果训练过于拟合,则数据只能适应训练数据,压缩效果反而适得其反。

五.总结
上面介绍了几种常用的降维方式,除此之外 Sklearn 包,AutoEncoder 变体还有多种降维方式,由于这里的数据都是基于随机数据生成且没有对应标识分类,所以可视化效果无法达到群簇的效果,如果有真实场景数据且可以拿到节点对应类别索引,可以在调用 plt.scatter(x, y, lable=c) 时添加 label = c的参数,这样同一类的点将会有同样的颜色,可以更直观的看到降维和聚类的效果。