图神经网络
我们现在大部分的工作都是建立一个条件之上-图神经网络的输入输入数据(图)是已知的。假设图是未知的,那么我们应该怎么生成图呢?

答案是:使用图生成模型(graph generative model)生成任务所需要的图。
不单是图未知的情况需要使用到图生成,还有以下几个原因:

学习图生成可以分为以下三步:

Properties of Real-world Graphs
真实图(相对于随机图)主要有以下几个重要属性:
- 度分布(Degree distribution) P ( k ) P(k) P(k)
- 聚类系数(Clustering coefficient) C C C
- 连通分量(Connected components) s s s
- 最短路径长度(Path length) h h h
度分布(Degree distribution)
P
(
k
)
P(k)
P(k)
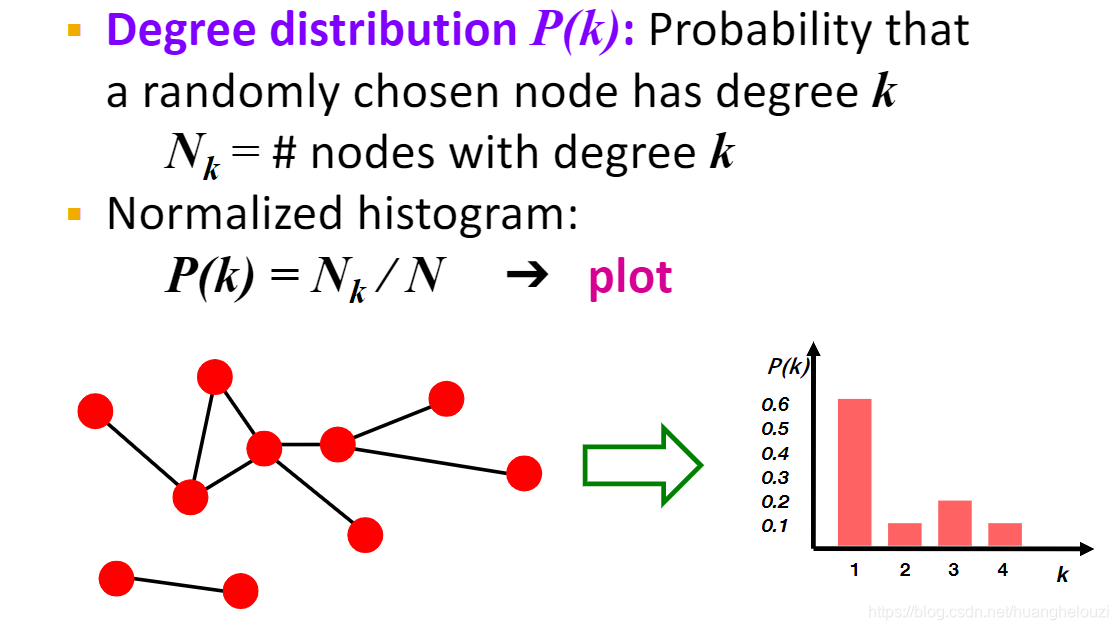
聚类系数(Clustering coefficient)
C
C
C
集聚系数(也称群聚系数、集群系数)是用来描述一个图中的顶点之间结集成团的程度的系数。在社交网络可理解为某个人的两个朋友之间成为朋友概率。
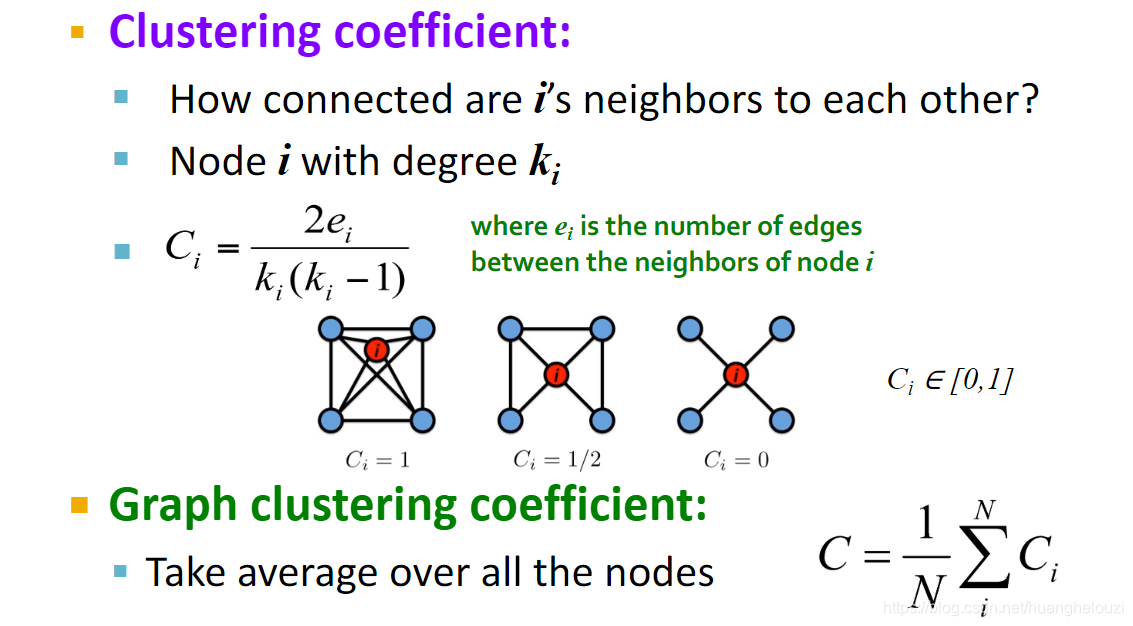
连通分量(Connected components)
s
s
s
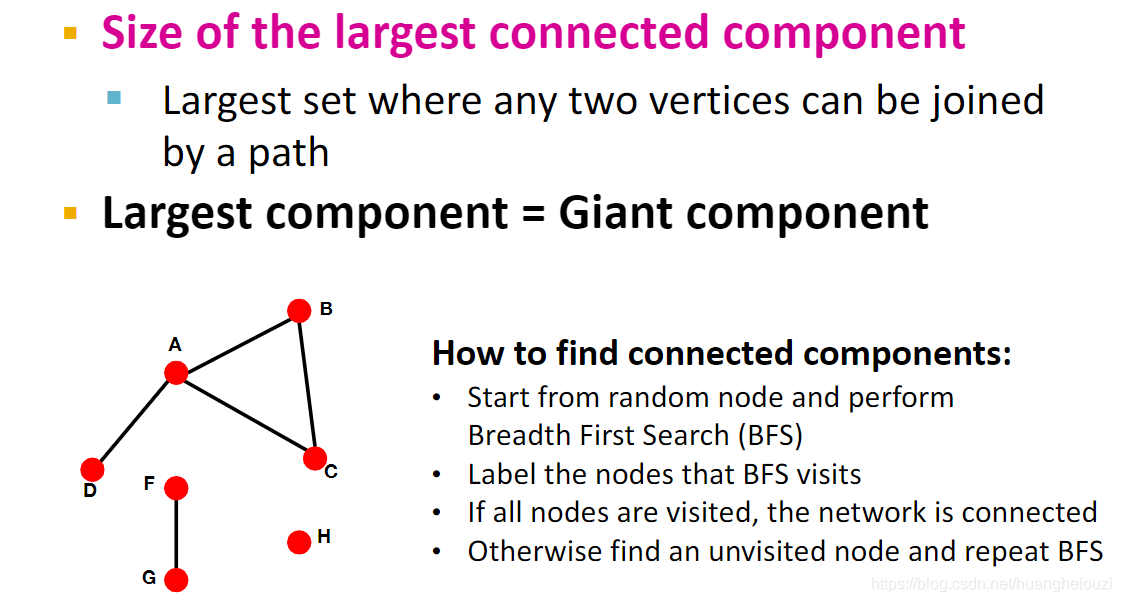
最短路径长度(Path length)
h
h
h
这里需要注意一个概率,就是图的直径(Diameter)指的是在图中各个节点对之间最短路径的最大值,不过为了考虑鲁棒性(防止图中有一个节点对的最短路径特别大,从而导致图的直径也变得特别大),一般取的是平均最短路径长度且忽略不连通的节点对的无限长距离。

下面以MSN网络为例,解释说明这几个图的属性。首先给出MSN网络的一些基本参数。

度分布(Degree distribution)
P
(
k
)
P(k)
P(k)
我们将度数和数量可视化之后,可发现该图的度服从幂律分布(其实绝大部分真实图的度都服从幂律分布)。
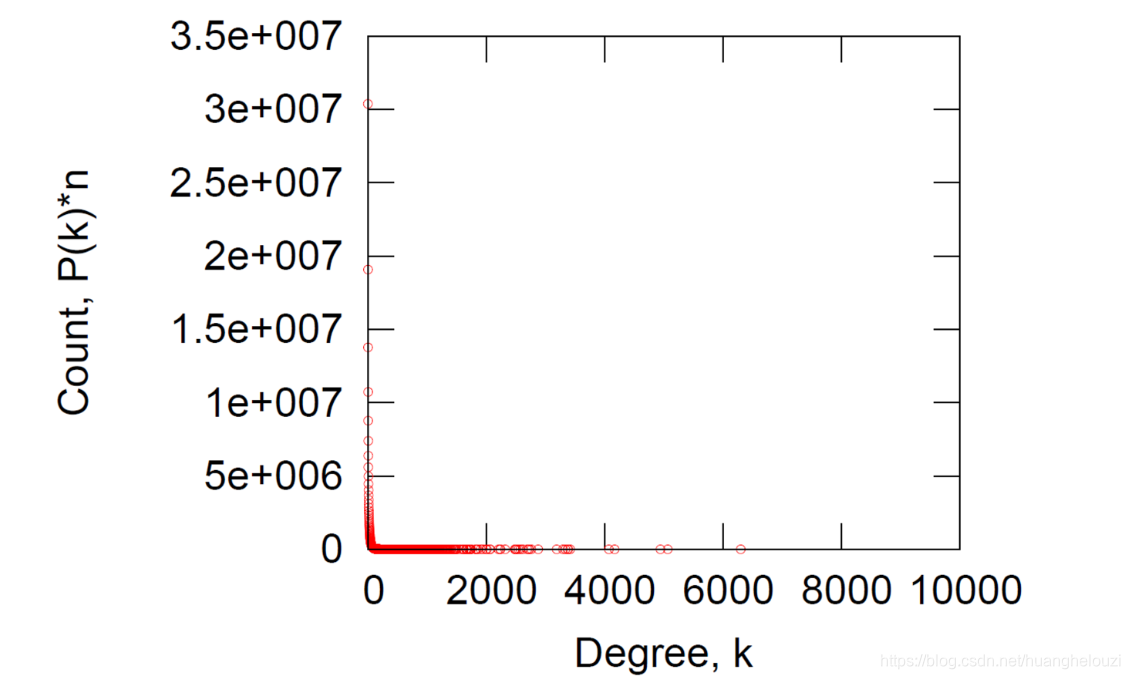
但是上面可以发现可视化效果不是很好,然后横纵坐标都设置为
1
0
k
10^k
10k次方的尺度使得我们更容易的进行可视化分析。
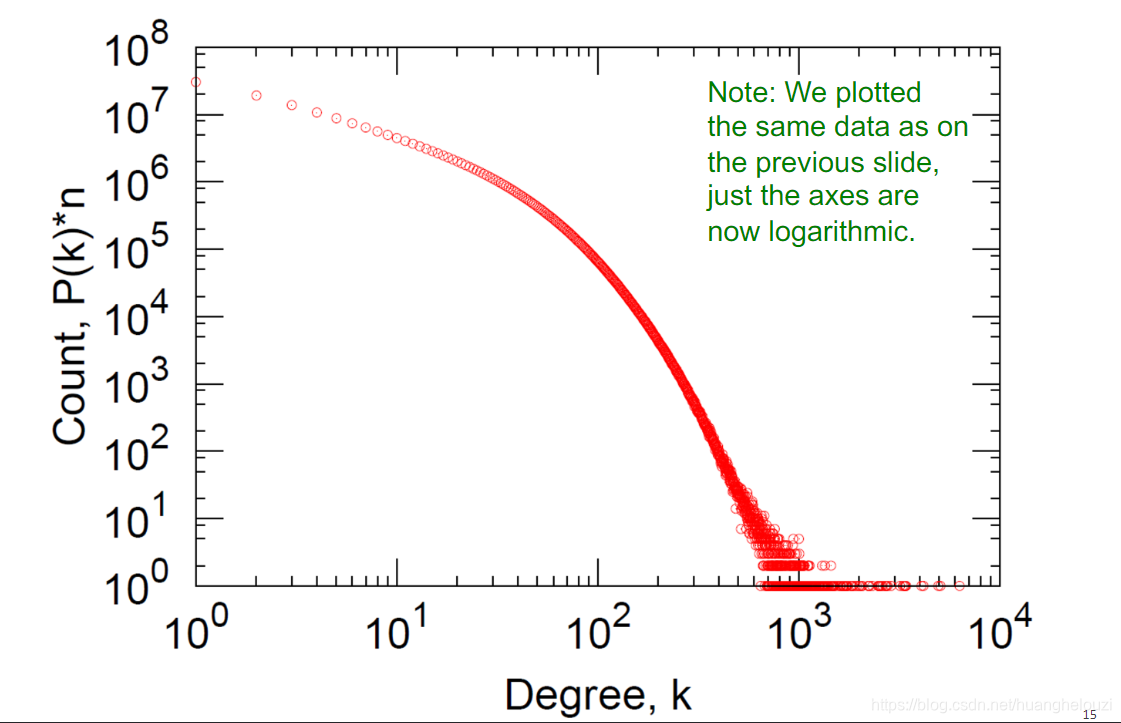
聚类系数(Clustering coefficient)
C
C
C
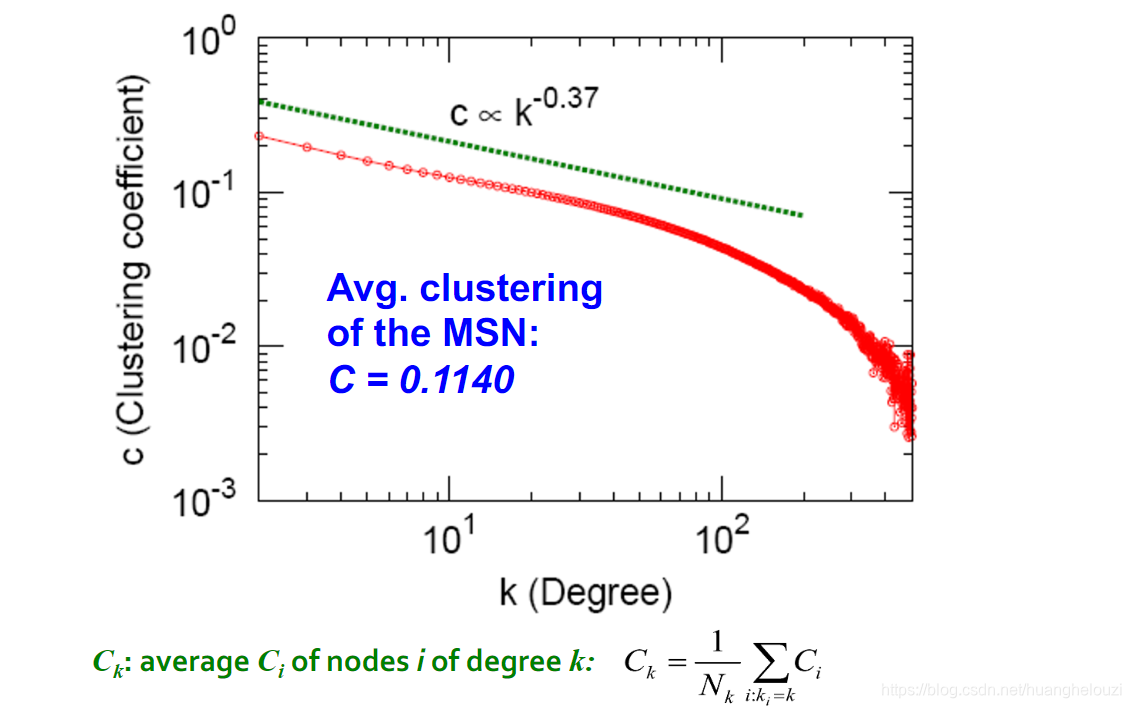
连通分量(Connected components)
s
s
s
从下图还可发现大小为1的连通分量个数约有
1
0
6
10^6
106个,也就是孤立节点约有
1
0
6
10^6
106个。
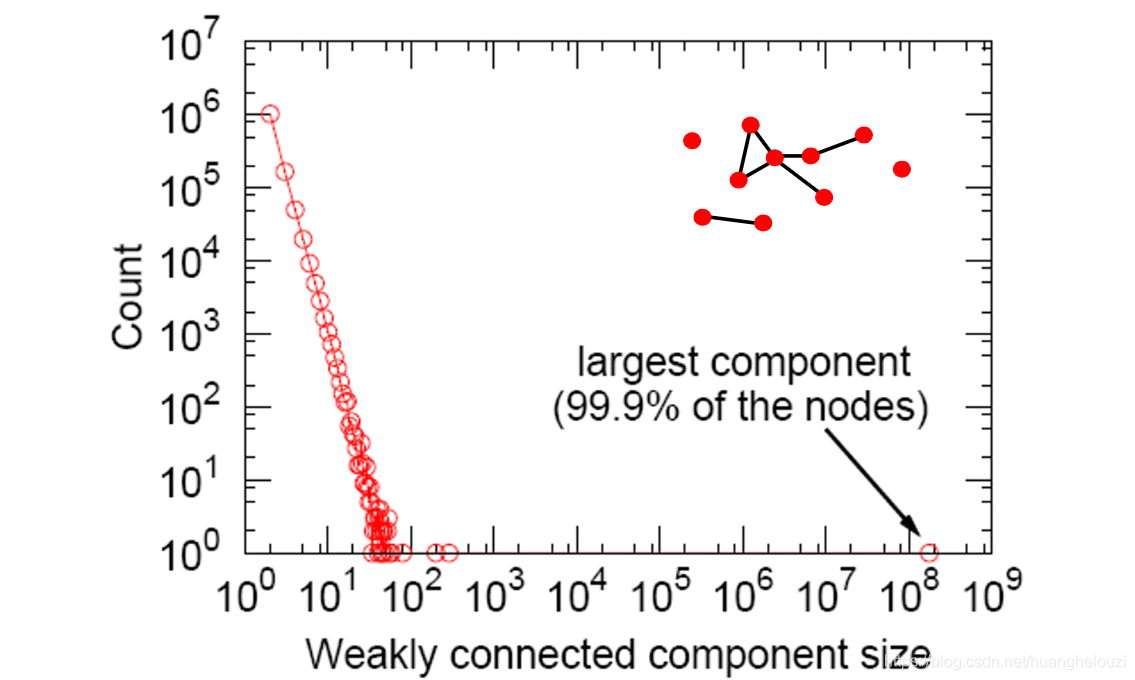
最短路径长度(Path length)
h
h
h
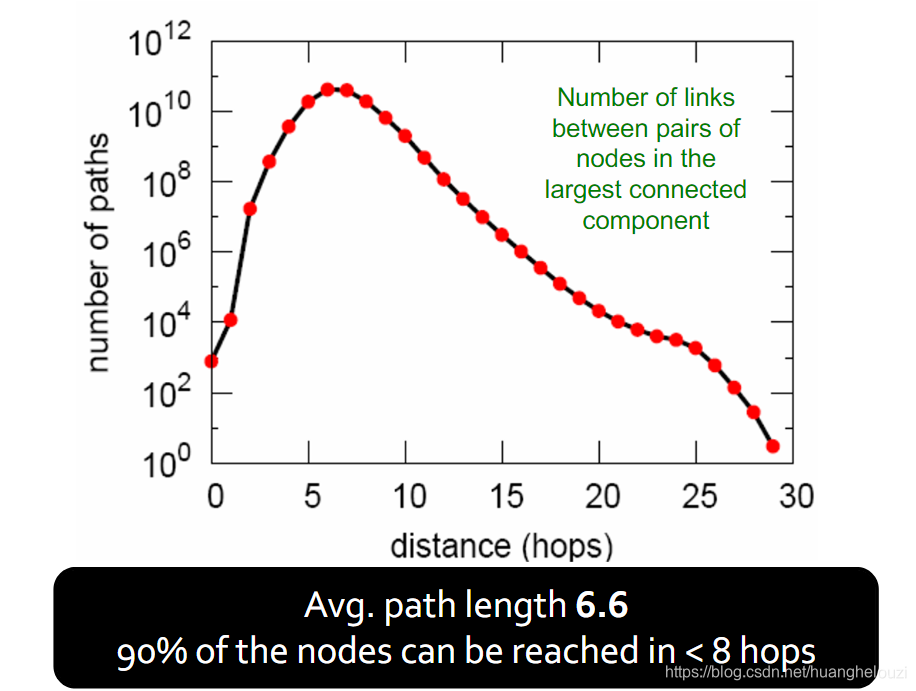
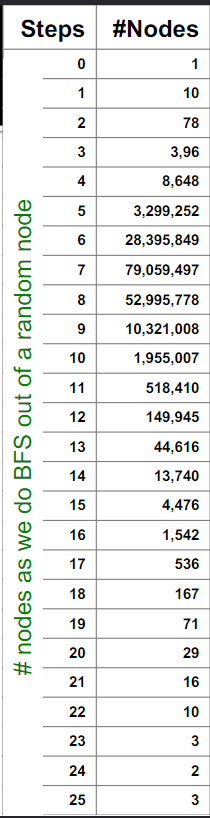
ER随机图
和社区检测(Community Detection)一样,图生成也需要一个对比模型,下面将更深入地学习ER随机图。
ER随机图有两个变体,其中一种比较常用的是:
G
n
p
G_{np}
Gnp?在有n个节点的无向图中,节点对间的边以概率p生成。

并且需要注意的是,参数n和p并不能唯一确定一个图。
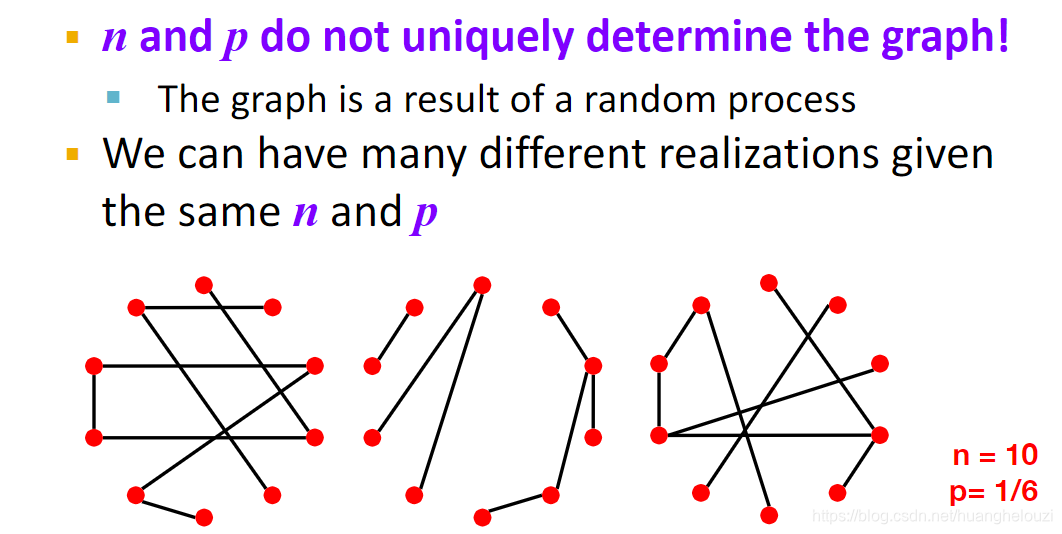
然后我们来看看随机图
G
n
p
G_{np}
Gnp?几大常用属性,且和真实图做个对比。
- 度分布(Degree distribution) P ( k ) P(k) P(k)
随机图
G
n
p
G_{np}
Gnp?很多属性都可以使用数学公式直接推导出来。
随机图的度分布服从二项分布,当n足够大时,可视为服从正态分布;真实图的度分布服从幂律分布。
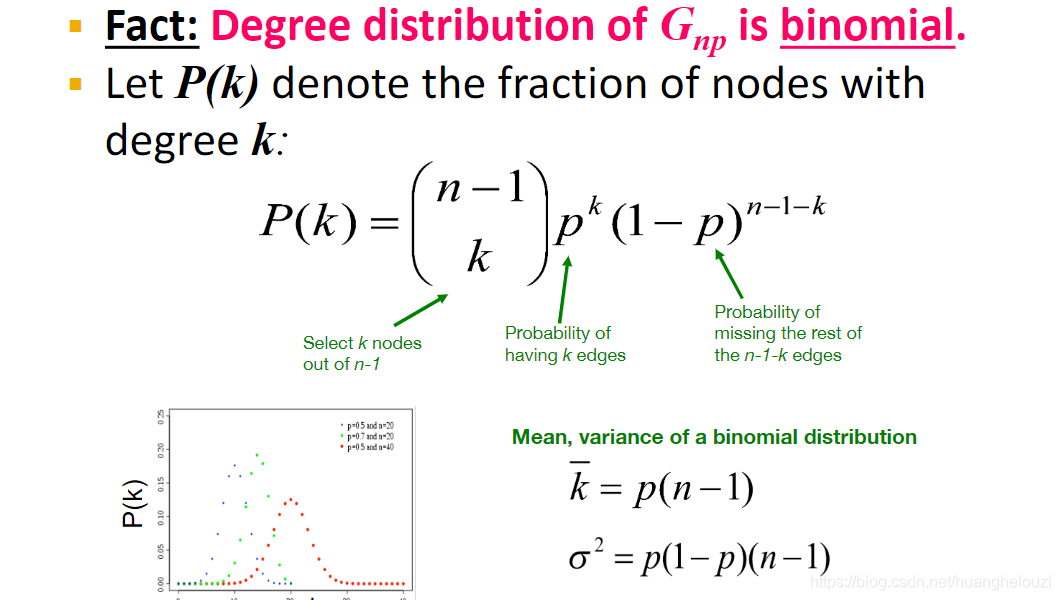
- 聚类系数(Clustering coefficient) C C C
随机图的聚类系数非常小,现实图比较大。

- 连通分量(Connected components)
s
s
s

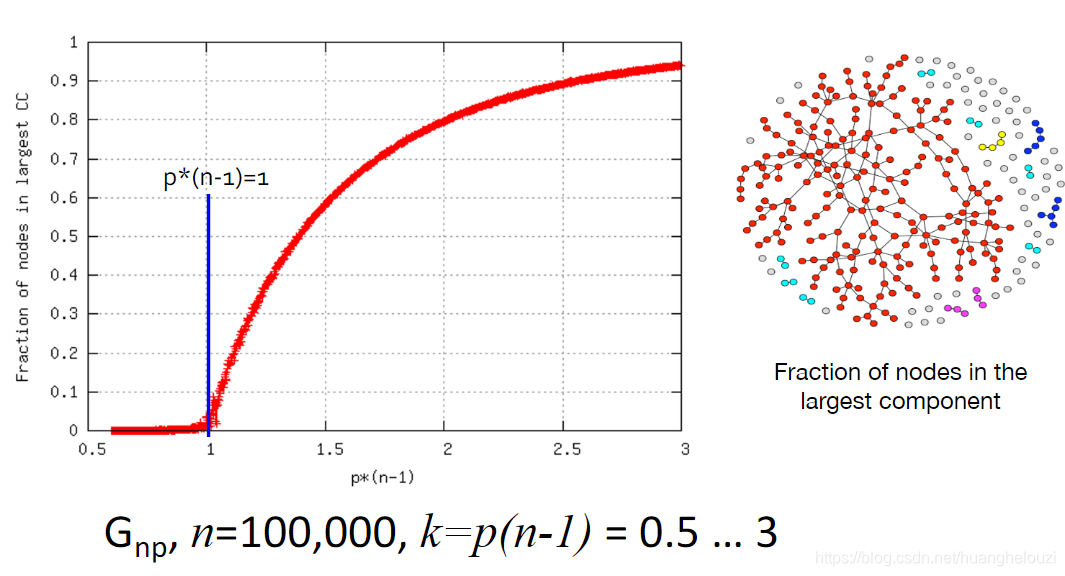
真实图和随机图主要在度分布和聚类系数上存在差异,而其他的属性,比如平均路径长度、度序列等都是类似。

The Small-World Model
ER模型生成的ER随机图有两个缺点:一是度分布服从二项分布;二是聚类系数过小。
而Small-World模型解决的就是ER随机图聚类系数过小的问题。Small-World模型生成的Small-World图可同时拥有正则图的High clustering coefficient和ER随机图的Low diameter的优点。
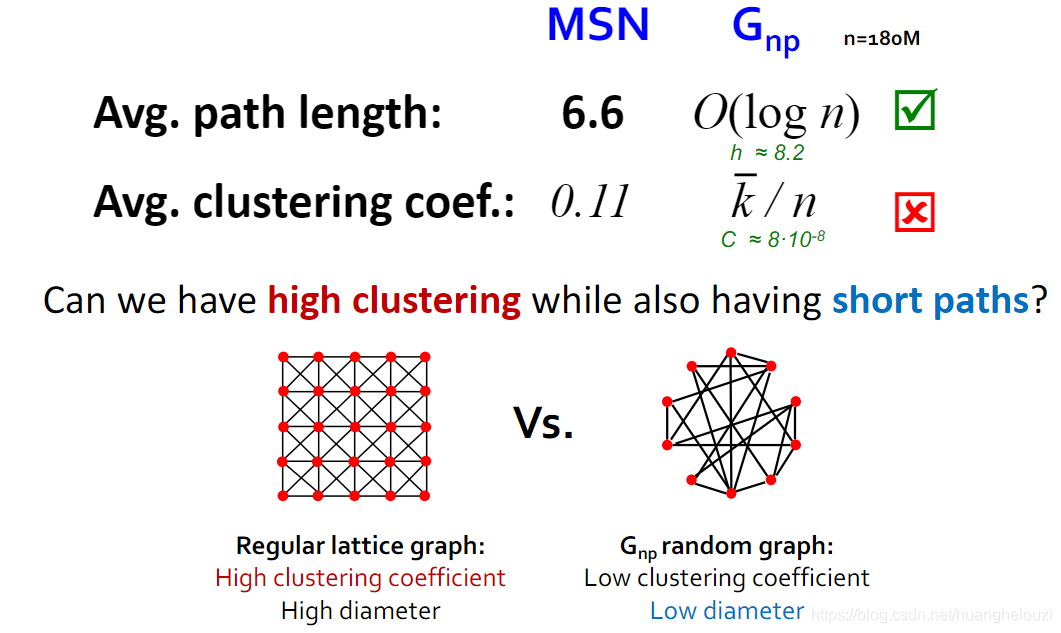
在MSN网络中,真实图比ER随机图的聚类系数高七个数量级。

Small-World图可同时拥有正则图和ER随机图的优点。
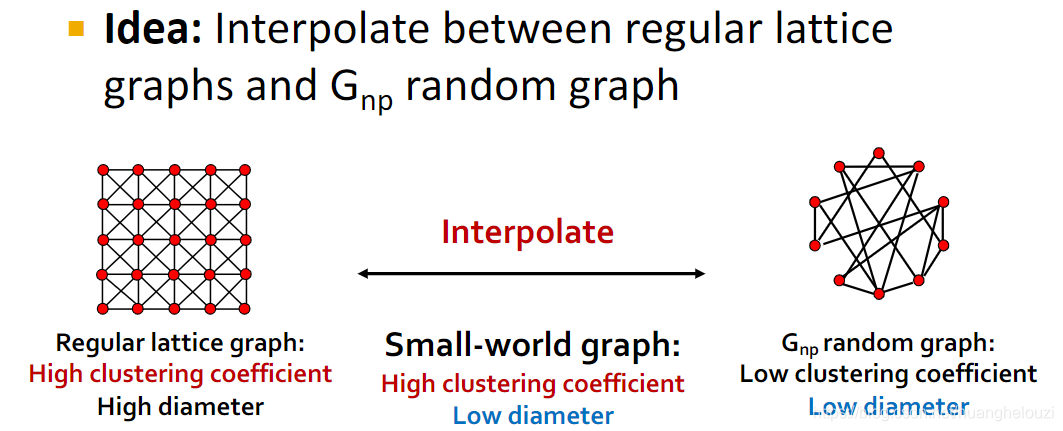
生成Small-World图主要分为两步:


需要注意的是,添加或者删除边会减小图的聚类系数,也可缩小图平均距离,我们需要对这两个条件进行折中。
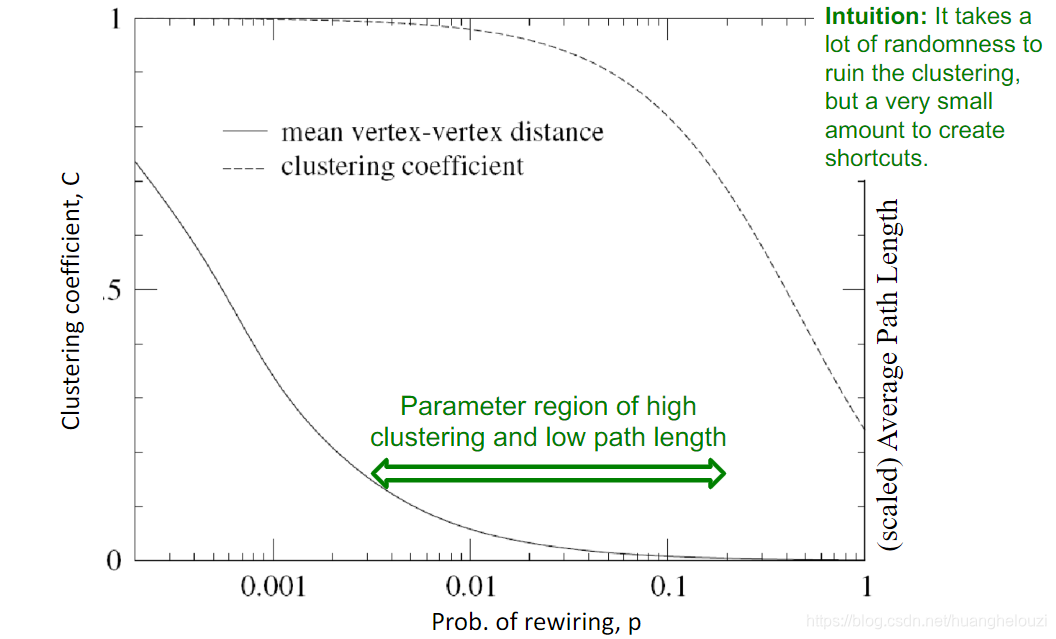
最后对小世界模型进行一个总结。

常见的传统图生成模型还有“Kronecker Graph Model”。