目录
机器学习类型和算法的分类

无监督学习的数据集中没有输出标签y,常用的无监督学习算法有聚类和降维。
概要
聚类人有归纳和总结的能力,机器也有。聚类就是让机器把数据集中的样本按照特征的性质分组,这个过程中没有标签的存在。
聚类和监督学习中的分类问题有些类似,其主要区别在于:传统分类问题也就是说,在对猫狗图像分类之前,我们心里面已经对猫、狗图像形成了概念。这些概念指导着我们为训练集设定好标签。机器首先是学习概念,然后才能够做分类、做判断。分类的结果,还要接受标签,也就是已有概念的检验。
而聚类不同,虽然本质上也是“分类”,但是“譬如,漫天繁星,彼此之间并没有关联,也 没有星座的概念,当人们看到它们,是先根据星星在广袤苍穹中的位置将其一组一组地“聚集"起来,然后才逐渐形成星座的概念。人们说,这一-组星星是“大熊座",那一组星星是“北斗七星”。这个先根据特征进行分组,之后再概念化的过程就是聚类。聚类算法有好几种,K均值(K-means)是其中最常见的一种。
一、K均值算法
K均值算法是最容易理解的无监督学习算法。算法简单,速度也不差,但需要人工指定K值,也就是分成几个聚类。
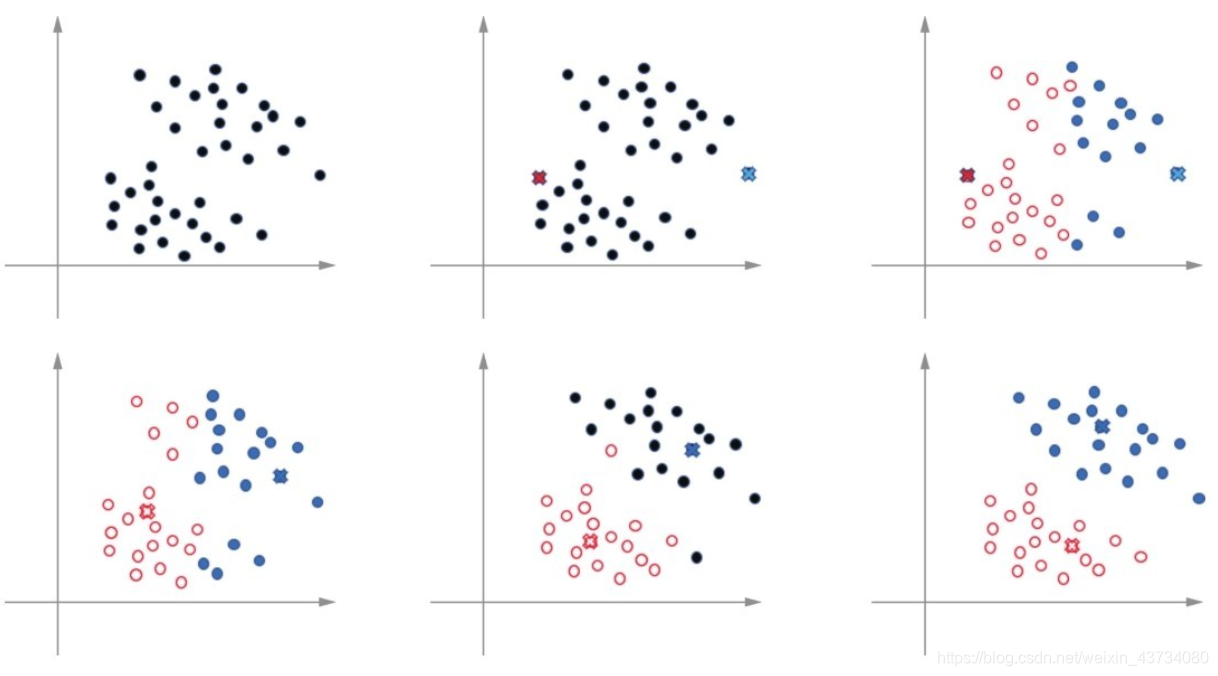
具体算法流程:
(1)首先确定K的数值,比如5个聚类,也叫5个簇。
(2)然后再一大堆数据中随机挑选K个数据点,作为簇的质心(centroid)。这些随机质心当然不完美,别着急,它们会慢慢变得完美。
(3)遍历集合中每一个数据点,计算它们与每一个质心的距离(比如欧式距离)。数据点离哪个质心近,就属于哪一类。此时初始的K个类别开始形成。
(4)这时每一个质心中都聚集了很多数据点,于是质心说,你们来了,我就要“退役”了(这是个伟大的“禅让制度”啊!),选取一个新的质心吧。然后计算出每一类中最靠近中心的点,作为新的质心。此时新的质心会比原来随机选来的靠谱一些(等会儿用图展示质心的移动)
(5)重新进行步骤(3),计算所有数据点和新的质心的距离,在新的质心周围形成新的簇分配(“吃瓜群众”随风飘摇,离谁进就跟谁)。
(6)重新进行步骤(4),继续选择更好的质心(一代一代的“禅让”下去)。
(7)一直重复进行步骤(5)和(6),不断更新簇中的数据点,不断找到新的质心,直至收敛。
二、K值的选取:手肘法
聚类问题的关键在于K值的选取。也就是说,把一批数据划分为多少个簇是最合理的呢?当数据特征维度较少、数据分布较为分散时,可通过数据可视化的方法来人工确定K值。但当数据特征维度较多、数据分布较为混乱时,数据可视化帮助不大。
当然,也可以经过多次实验,逐步调整,使簇的数目逐渐达到最优,以符合数据集的特点。
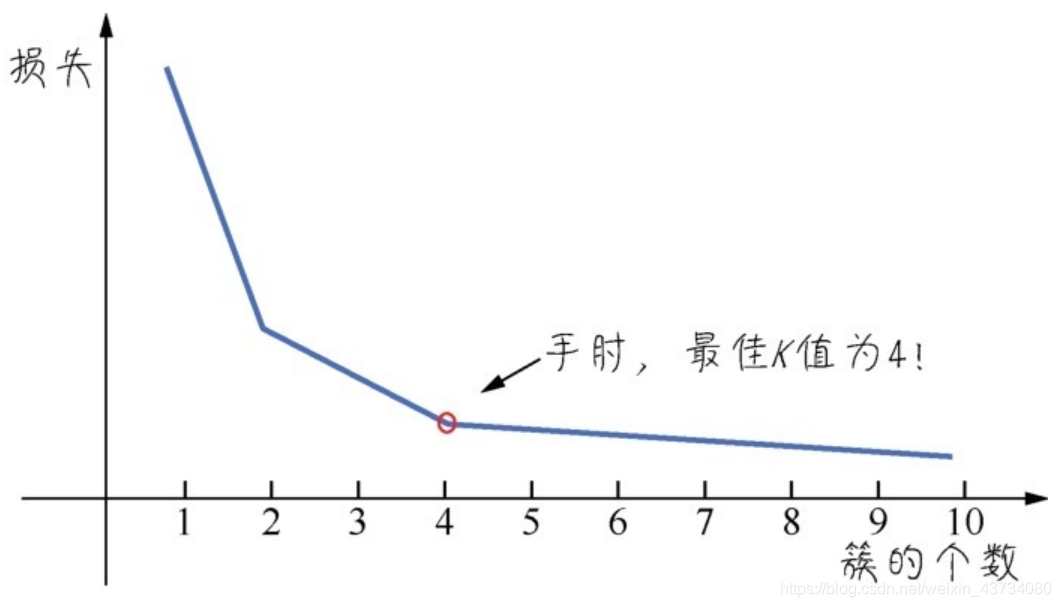
这里我介绍一种直观的手肘法( elbow method)进行簇的数量的确定。手肘法是基于 对聚类效果的一一个度量指标来实现的,这个指标也可以视为一一种损失。 在K值很小的时候,整体损失很大,而随着K值的增大,损失函数的值会在逐渐收敛之前出现一个拐点。此时的K值就是比较好的值。
大家看下面的图,损失随着簇的个数而收敛的曲线有点像只手臂,最佳K值的点像是手肘,因此取名为手肘法。
三、用聚类实现鸢尾花数据分类
1. 数据读取
import numpy as np
import pandas as pd
dataset = pd.read_csv('D:/NoteBook/Iris.txt')
dataset.head()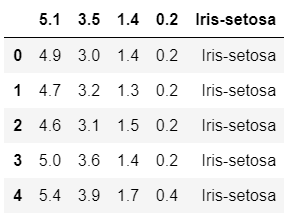
#只对两个特征进行聚类,以便二维展示
X = dataset.iloc[:,[0,3]].values下面尝试用不同的K值进行聚类的拟合
#聚类的集合,下面尝试用不同的K值进行聚类的拟合
from sklearn.cluster import KMeans#导入聚类模型
cost = []#初始化损失(距离)值
for i in range(1,11):#尝试不同的K值
kmeans = KMeans(n_clusters= i ,init='k-means++', random_state = 0)
kmeans.fit(X)
cost.append(kmeans.inertia_)#inerita_是我们选择的方法,其作用相当于损失函数#绘制手肘图找到最佳K值
import matplotlib.pyplot as plt
import seaborn as sns
hist,ax = plt.subplots()
plt.plot(range(1,11),cost)
# plt.title('The Elbow Method')
ax.set_title('The Elbow Method')
ax.set_ylabel('Cost')
plt.show()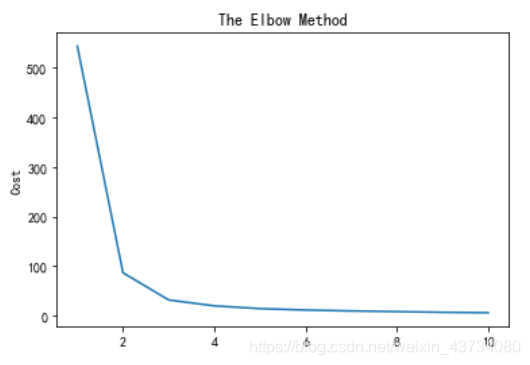
kmeansmodel = KMeans(n_clusters=3, init='k-means++')
y_kmeans = kmeansmodel.fit_predict(X)#把分类好的聚类可视化
hist,ax = plt.subplots()
plt.scatter(X[y_kmeans == 0,0], X[y_kmeans == 0,1],s = 100, c = 'cyan', label = 'Cluster 1')#聚类1
plt.scatter(X[y_kmeans == 1,0], X[y_kmeans == 1,1],s = 100, c = 'blue', label = 'Cluster 2')#聚类2
plt.scatter(X[y_kmeans == 2,0], X[y_kmeans == 2,1],s = 100, c = 'green', label = 'Cluster 3')#聚类3
plt.scatter(kmeans.cluster_centers_[:,0],kmeans.cluster_centers_[:,1],s = 200, c = 'yellow', label = 'Centroids')#质心
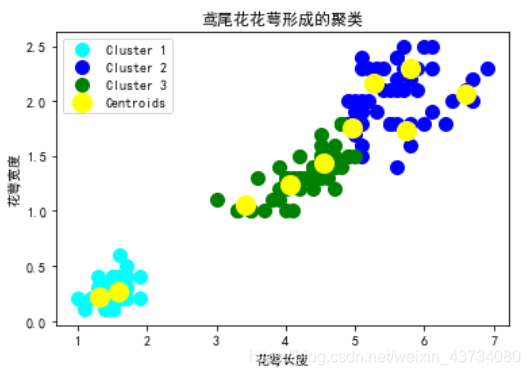
ax.set_title('鸢尾花花萼形成的聚类')#鸢尾花花萼形成的聚类
ax.set_xlabel('花萼长度')#
ax.set_ylabel('花萼宽度')#
plt.legend()
plt.show()打印聚类结果图:?
四、应用案例
本案例主要是基于企业注册资金和参保人数的企业聚类分析
1. 读取数据
import numpy as np
import pandas as pd
data = pd.read_excel('C:/新评分及数据补全合并.xlsx')
data.head()注册资金数据去单位
import re
io = 'C:/新评分及数据补全合并.xlsx'
registered_capital = data['注册资本']
capital = []
for i in registered_capital:
m = str(i).replace('-','0') #匹配到“-”并替换为“0”
now = re.match("\d*", m).group() #group(0) 同 group() 就是匹配正则表达式整体结果
capital.append(now)
data['注册资本新'] = pd.DataFrame(capital) #数据存入Excel列
data['注册资本新'].head()
data.to_excel(io) #此行代码为数据存入Excel列,上面已存储,可注释 数据归一化处理
from sklearn.preprocessing import MinMaxScaler
io = 'C:/新评分及数据补全合并.xlsx'
x1 = data[['注册资本新']]
x2 = data[['参保人数']]
# x2 = (x1 - np.min(x1))/(np.max(x1) - np.min(x1)) #注册资本归一化后的结果
min_max_scaler = MinMaxScaler()
X_train_minmax1 = min_max_scaler.fit_transform(x1)#注册资本归一化后的结果
X_train_minmax2 = min_max_scaler.fit_transform(x2)#参保人数归一化后的结果
data['注册资本归一化'] = pd.DataFrame(X_train_minmax1) #数据存入Excel列
data['参保人数一化'] = pd.DataFrame(X_train_minmax2) #数据存入Excel列
# pd.DataFrame(X_train_minmax1.tolist()).describe()
# pd.DataFrame(X_train_minmax2.tolist()).describe()
# data.to_excel(io) 归一化结果
X2 = data.loc[:,['注册资本归一化','参保人数一化']].values
print(X2)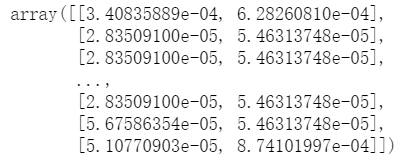 ?
?
2. 绘制手肘图
#绘制手肘图
from sklearn.cluster import KMeans
cost = []
for i in range(1,11):
kmeans = KMeans(n_clusters= i ,init='k-means++', random_state = 0)
kmeans.fit(X2)
cost.append(kmeans.inertia_)3. 找到最佳K值
#绘制手肘图找到最佳K值
import matplotlib.pyplot as plt
import seaborn as sns
hist,ax = plt.subplots()
plt.plot(range(1,11),cost)
# plt.title('The Elbow Method')
ax.set_title('The Elbow Method')
ax.set_ylabel('Cost')
plt.show()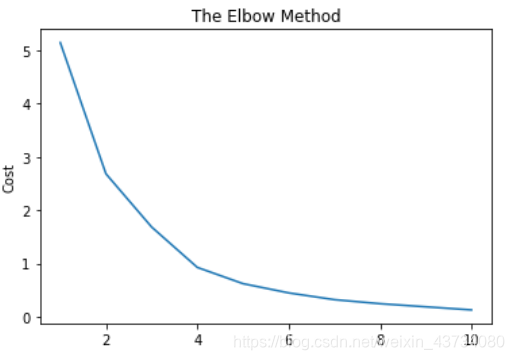
由手肘图可判断,最佳K值大概为4,我们选择4作为聚类个数
kmeansmodel = KMeans(n_clusters=4, init='k-means++')
y_kmeans = kmeansmodel.fit_predict(X2)4. 分类结果可视化
#把分类好的聚类可视化
hist,ax = plt.subplots()
#解决中文显示问题
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.scatter(X2[y_kmeans == 0,0], X2[y_kmeans == 0,1],s = 100, c = 'cyan', label = 'Cluster 1')#聚类1
plt.scatter(X2[y_kmeans == 1,0], X2[y_kmeans == 1,1],s = 100, c = 'blue', label = 'Cluster 2')#聚类2
plt.scatter(X2[y_kmeans == 2,0], X2[y_kmeans == 2,1],s = 100, c = 'green', label = 'Cluster 3')#聚类3
plt.scatter(X2[y_kmeans == 3,0], X2[y_kmeans == 3,1],s = 100, c = 'red', label = 'Cluster 4')#聚类3
plt.scatter(kmeans.cluster_centers_[:,0],kmeans.cluster_centers_[:,1],s = 200, c = 'yellow', label = 'Centroids')#质心
ax.set_title('企业聚类')#客户形成的聚类
ax.set_xlabel('注册资本')#
ax.set_ylabel('参保人数')#
plt.legend()
plt.show()企业聚类结果
 ?
?
?由于我们的数据比较随机,并不是很规整,所以结果来看,聚类结果并不是十分美观。