[人工智能]六、神经网络

六、神经网络

内容参考来自https://github.com/dragen1860/Deep-Learning-with-TensorFlow-book开源书籍《TensorFlow2深度学习》，这只是我做的简单的学习笔记，方便以后复习

1.感知机全连接层

张量方式实现

# 创建 W,b 张量
x = tf.random.normal([2,784])
w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1))
b1 = tf.Variable(tf.zeros([256]))
o1 = tf.matmul(x,w1) + b1 # 线性变换
o1 = tf.nn.relu(o1) # 激活函数

层方式实现

x = tf.random.normal([4,28*28])
from tensorflow.keras import layers # 导入层模块
# 创建全连接层，指定输出节点数和激活函数
fc = layers.Dense(512, activation=tf.nn.relu)
h1 = fc(x) # 通过 fc 类实例完成一次全连接层的计算，返回输出张量

可以通过类的tf.trainable_variables 来返回待优化参数列表。

可以通过tf.non_trainable_variables 成员返回所有不需要优化的参数列表。

如果希望获得所有参数列表，可以通过类的 tf.variables 返回所有内部张量列表。

2.神经网络

张量方式实现

# 隐藏层 1 张量
w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1))
b1 = tf.Variable(tf.zeros([256]))
# 隐藏层 2 张量
w2 = tf.Variable(tf.random.truncated_normal([256, 128], stddev=0.1))
b2 = tf.Variable(tf.zeros([128]))
# 隐藏层 3 张量
w3 = tf.Variable(tf.random.truncated_normal([128, 64], stddev=0.1))
b3 = tf.Variable(tf.zeros([64]))
# 输出层张量
w4 = tf.Variable(tf.random.truncated_normal([64, 10], stddev=0.1))
b4 = tf.Variable(tf.zeros([10]))
with tf.GradientTape() as tape: # 梯度记录器
    # x: [b, 28*28]
    # 隐藏层 1 前向计算，[b, 28*28] => [b, 256]
    h1 = x@w1 + tf.broadcast_to(b1, [x.shape[0], 256])
    h1 = tf.nn.relu(h1)
    # 隐藏层 2 前向计算，[b, 256] => [b, 128]
    h2 = h1@w2 + b2
    h2 = tf.nn.relu(h2)
    # 隐藏层 3 前向计算，[b, 128] => [b, 64]
    h3 = h2@w3 + b3
    h3 = tf.nn.relu(h3)
    # 输出层前向计算，[b, 64] => [b, 10]
    h4 = h3@w4 + b4

层方式实现

# 导入 Sequential 容器
from tensorflow.keras import layers,Sequential
# 通过 Sequential 容器封装为一个网络类
model = Sequential([
    layers.Dense(256, activation=tf.nn.relu) , # 创建隐藏层 1
    layers.Dense(128, activation=tf.nn.relu) , # 创建隐藏层 2
    layers.Dense(64, activation=tf.nn.relu) , # 创建隐藏层 3
    layers.Dense(10, activation=None) , # 创建输出层
])
# 前向计算时只需要调用一次网络大类对象，即可完成所有层的按序计算：
out = model(x) # 前向计算得到输出

3.激活函数

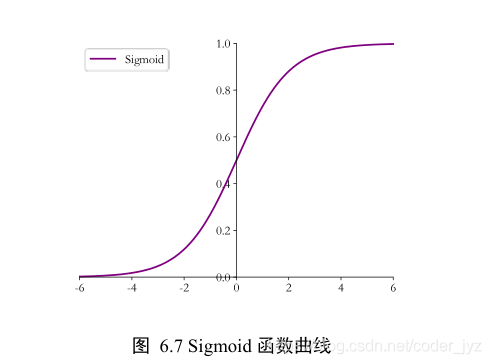
3.1Sigmoid

Sigmoid 函数也叫 Logistic 函数，定义为

$$Sigmoid(x)=\frac{1}{1+e^{?x}}$$

它的一个优良特性就是能够把𝑦 ∈ 𝑆的输入“压缩”到𝑦 ∈ (0,1)区间，这个区间的数值在机器学习常用来表示以下意义

• 概率分布 (0,1)区间的输出和概率的分布范围[0,1]契合，可以通过 Sigmoid 函数将输出转译为概率输出。
• 信号强度 一般可以将 0~1 理解为某种信号的强度，如像素的颜色强度，1 代表当前通道颜色最强，0 代表当前通道无颜色；抑或代表门控值(Gate)的强度，1 代表当前门控全部开放，0 代表门控关闭。

x = tf.linspace(-6.,6.,10)
tf.nn.sigmoid(x) # 通过 Sigmoid 函数

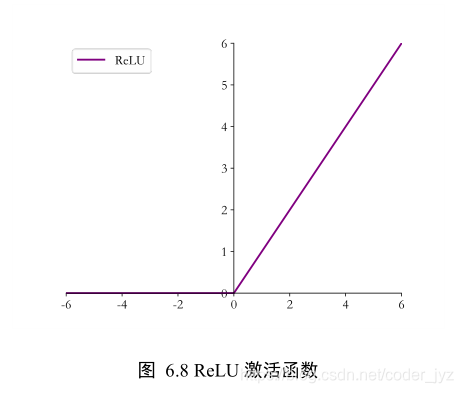
3.2ReLU

ReLU(𝑦) ? max(0,𝑦)可以看到，ReLU 对小于 0 的值全部抑制为 0；对于正数则直接输出，这种单边抑制特性来源于生物学。

tf.nn.relu(x) # 通过 ReLU 激活函数

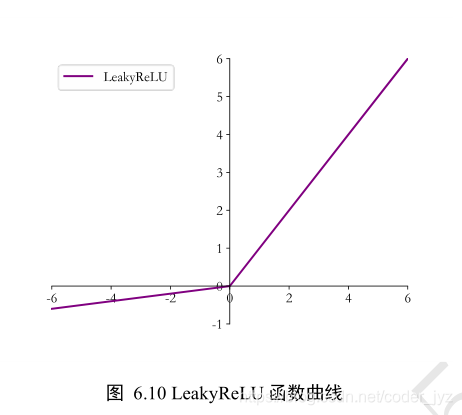
3.3LeakyReLU

ReLU 函数在𝑦 < 0时导数值恒为 0，也可能会造成梯度弥散现象，为了克服这个问题，LeakyReLU 函数被提出，如图

6.10 所示，LeakyReLU 的表达式为:

$$LeakyReLU=\{\begin{array}{ll}x,& \text{x>=0}\\ px,& \text{x<0}\end{array}$$

tf.nn.leaky_relu(x, alpha=0.1) # 通过 LeakyReLU 激活函数

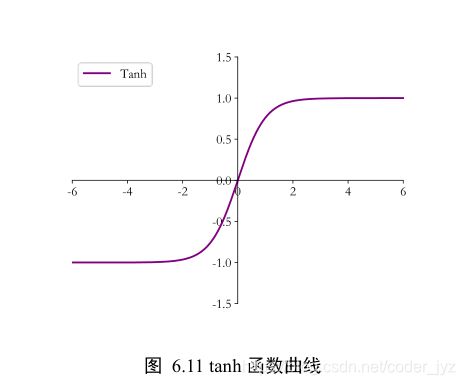
3.4Tanh

Tanh 函数能够将𝑦 ∈ 𝑆的输入“压缩”到(?1,1)区间，定义为

$$tanh(x)=\frac{e^x?e^{?x}}{e^x+e^{?x}}$$

tf.nn.tanh(x) # 通过 tanh 激活函数

4.输出层设计

4.1普通实数空间

这一类问题比较普遍，像正弦函数曲线预测、年龄的预测、股票走势的预测等都属于整个或者部分连续的实数空间，输出层可以不加激活函数。

4.2[0, 1] 区间

输出值属于[0,1]区间也比较常见，比如图片的生成、二分类问题等。在机器学习中，一般会将图片的像素值归一化到[0,1]区间，如果直接使用输出层的值，像素的值范围会分布在整个实数空间。为了让像素的值范围映射到[0,1]的有效实数空间，需要在输出层后添加某个合适的激活函数𝜎，其中 Sigmoid 函数刚好具有此功能。

4.3[0,1] 区间，和为 1

输出值𝑝 𝑗 ∈ [0,1]，且所有输出值之和为 1，这种设定以多分类问题最为常见。可以通过在输出层添加 Softmax 函数实现。

在 Softmax 函数的数值计算过程中，容易因输入值偏大发生数值溢出现象；在计算交叉熵时，也会出现数值溢出的问题。为了数值计算的稳定性，TensorFlow 中提供了一个统一的接口，将 Softmax 与交叉熵损失函数同时实现，同时也处理了数值不稳定的异常，一般推荐使用这些接口函数，避免分开使用 Softmax 函数与交叉熵损失函数。函数式接口为
tf.keras.losses.categorical_crossentropy(y_true, y_pred, from_logits=False)，其中 y_true 代表了One-hot 编码后的真实标签，y_pred 表示网络的预测值，当 from_logits 设置为 True 时，y_pred 表示须为未经过 Softmax 函数的变量 z；当 from_logits 设置为 False 时，y_pred 表示为经过 Softmax 函数的输出。为了数值计算稳定性，一般设置 from_logits 为 True，此时tf.keras.losses.categorical_crossentropy 将在内部进行 Softmax 函数计算，所以不需要在模型中显式调用 Softmax 函数。

z = tf.random.normal([2,10]) # 构造输出层的输出
y_onehot = tf.constant([1,3]) # 构造真实值
y_onehot = tf.one_hot(y_onehot, depth=10) # one-hot 编码
# 输出层未使用 Softmax 函数，故 from_logits 设置为 True
# 这样 categorical_crossentropy 函数在计算损失函数前，会先内部调用 Softmax 函数
loss = keras.losses.categorical_crossentropy(y_onehot,z,from_logits=True)
loss = tf.reduce_mean(loss) # 计算平均交叉熵损失

4.4[-1, 1]

如果希望输出值的范围分布在(?1,1)区间，可以简单地使用 tanh 激活函数。

x = tf.linspace(-6.,6.,10)
tf.tanh(x) # tanh 激活函数

5.误差计算

常见的误差函数有均方差、交叉熵、KL 散度、Hinge Loss 函数等，其中均方差函数和交叉熵函数在深度学习中比较常见，均方差函数主要用于回归问题，交叉熵函数主要用于分类问题。

均方差误差函数

o = tf.random.normal([2,10]) # 构造网络输出
y_onehot = tf.constant([1,3]) # 构造真实值
y_onehot = tf.one_hot(y_onehot, depth=10)
loss = keras.losses.MSE(y_onehot, o) # 计算均方差

交叉熵误差函数

# 输出层未使用Softmax函数，故from_logits设置为True
loss = keras.losses.categorical_crossentropy(y_onehot,z,from_logits=True)

6.神经网络类型

6.1 卷积神经网络

其中比较流行的模型有用于图片分类的 AlexNet、VGG、GoogLeNet、ResNet、DenseNet 等，用于目标识别的 RCNN、Fast RCNN、Faster RCNN、Mask RCNN、YOLO、SSD 等。

6.2 循环神经网络

其中比较流行的模型有LSTM 模型、GRU、双向 RNN 等。

6.3 注意力( 机制)网络

RNN 并不是自然语言处理的最终解决方案，近年来随着注意力机制(AttentionMechanism)的提出，克服了 RNN 训练不稳定、难以并行化等缺陷，在自然语言处理和图片生成等领域中逐渐崭露头角。注意力机制最初在图片分类任务上提出，但逐渐开始侵蚀NLP 各大任务。2017 年，Google 提出了第一个利用纯注意力机制实现的网络模型Transformer，随后基于 Transformer 模型相继提出了一系列的用于机器翻译的注意力网络模型，如 GPT、BERT、GPT-2 等。在其它领域，基于注意力机制，尤其是自注意力(Self-Attention)机制构建的网络也取得了不错的效果，比如基于自注意力机制的 BigGAN 模型等。

6.4 图卷积神经网络

图片、文本等数据具有规则的空间、时间结构，称为 Euclidean Data(欧几里德数据)。卷积神经网络和循环神经网络被证明非常擅长处理这种类型的数据。而像类似于社交网络、通信网络、蛋白质分子结构等一系列的不规则空间拓扑结构的数据，它们显得力不从心。2016 年，Thomas Kipf 等人基于前人在一阶近似的谱卷积算法上提出了图卷积网络(Graph Convolution Network，GCN)模型。GCN 算法实现简单，从空间一阶邻居信息聚合的角度也能直观地理解，在半监督任务上取得了不错效果。随后，一系列的网络模型相继被提出，如 GAT，EdgeConv，DeepGCN 等。

7. 题外话

最近整理笔记发现为啥有抄书的感觉，很奇怪，千万不要本末倒置啊。。。。