[人工智能]李宏毅机器学习（30）

Q-Learing

Critic

相比于Policy，Critics的评价方法很不一样：他有一个状态评价函数$V^{\pi }$，输入是Environment的一个状态State，然后根据Actor也就是$\pi$的情况，输出从当前这个状态开始到结束，一共能获得多少期望的Reward，记为$V^{\pi }(s)$。
比如打砖块时，$V^{\pi }$会输出从现在到结束大概能得多少分。
比如下围棋，$V^{\pi }$会输出现在的局势下双方胜率是多少。

那么，如何做这个$V^{\pi }$呢？一般有两种办法。

第一种，蒙特卡洛法。先观察$\pi$玩很多次游戏。然后看到一个state后将结果尽量向某一局游戏结果贴合。

第二种，时序查分算法。我们只需要知道从状态$s_a$到状态$s_b$需要做Action$a$，获得Reward$r$。那我们就可以训练一个Network，让$V^{\pi }(s_b)?V^{\pi }(s_a)$尽可能接近$r$。

以实例来说明两者之间的差别。
目前多数使用TD，MC很少用了。

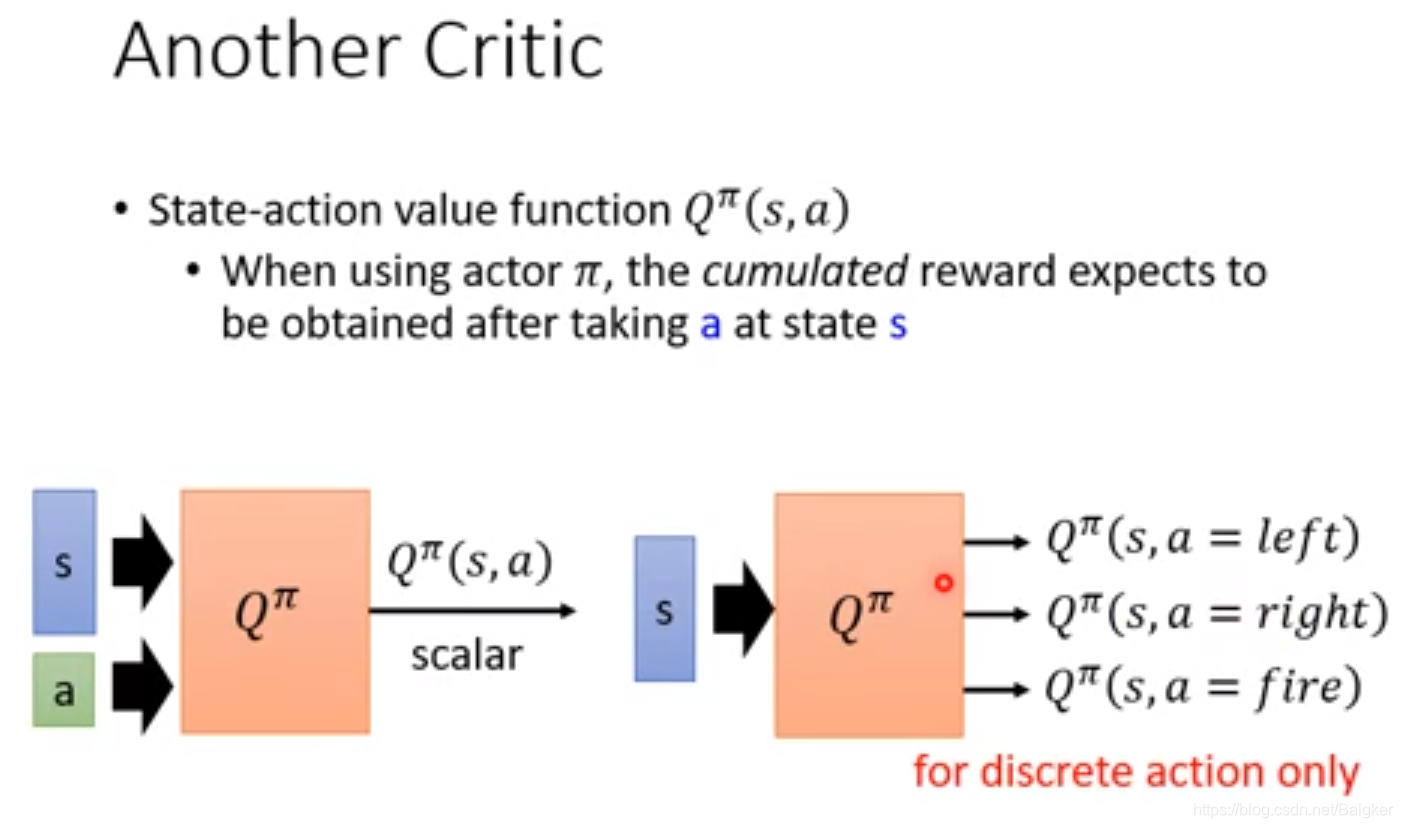
还有一种Critic的方法。用$Q^{\pi }(s,a)$在某个状态s采取了行动a之后会得到累计的Reward。
这就是Q-Learning。

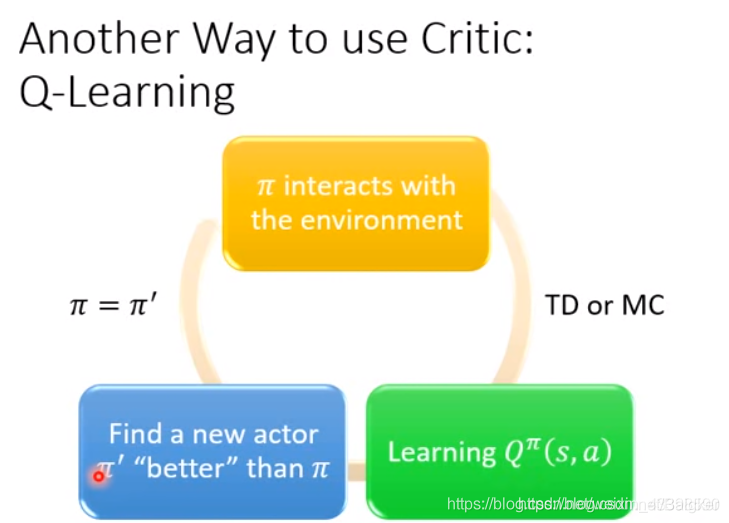
Q-learning的思路就是通过与环境互动使用更好的$\pi$。而且，只要求出$Q^{\pi }(s,a)$就一定能找到一个更好的Actor$\pi$。

什么是更好的Actor呢？对于任意的状态s，都有：

实际上，${\pi }^{\prime }$并没有额外的参数或者另一个神经网络去表示，它只是依靠$Q$推导出来的。
注意： 如果动作是一个连续值的话则不适合使用这种方法。

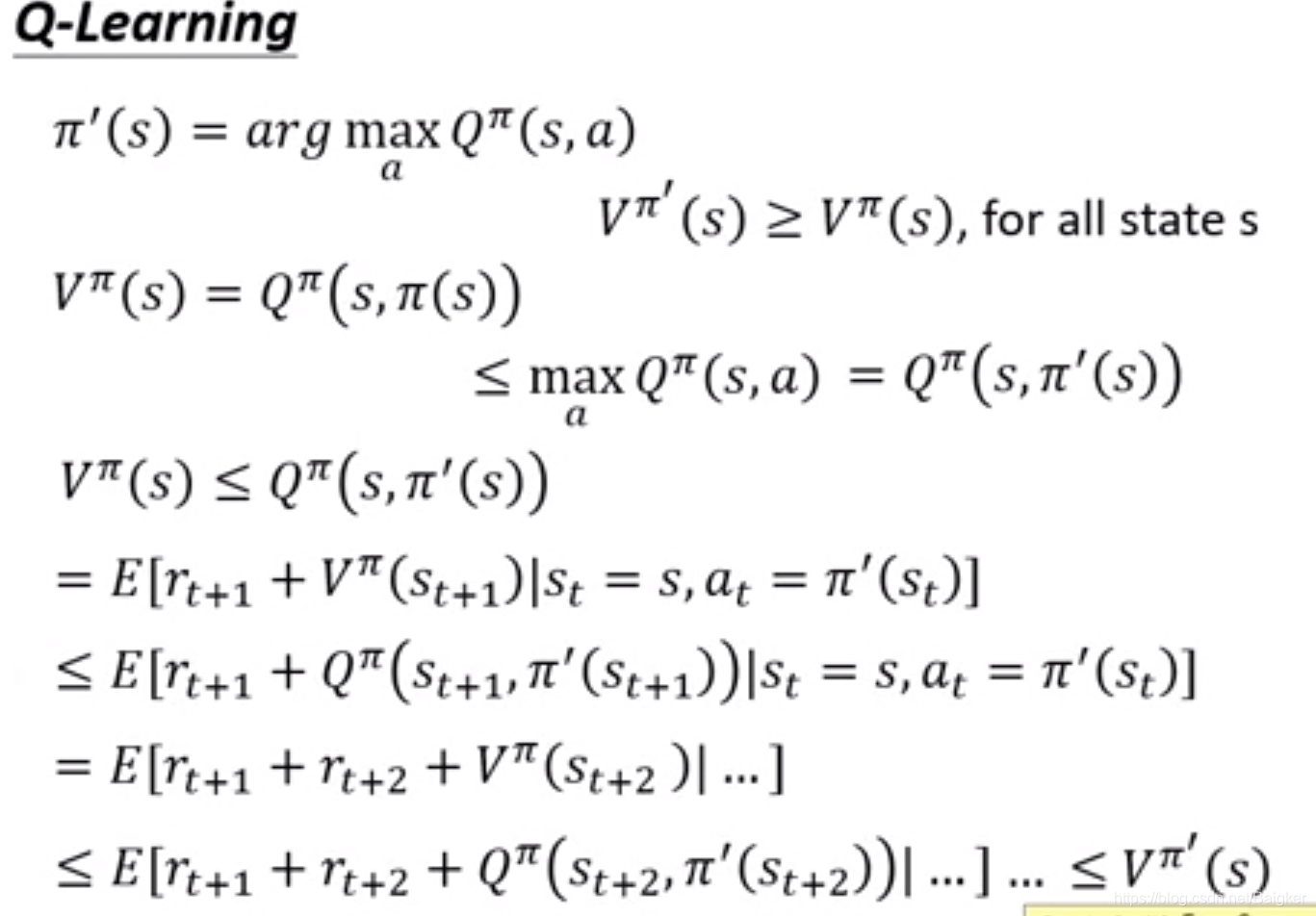
Q-learning技巧

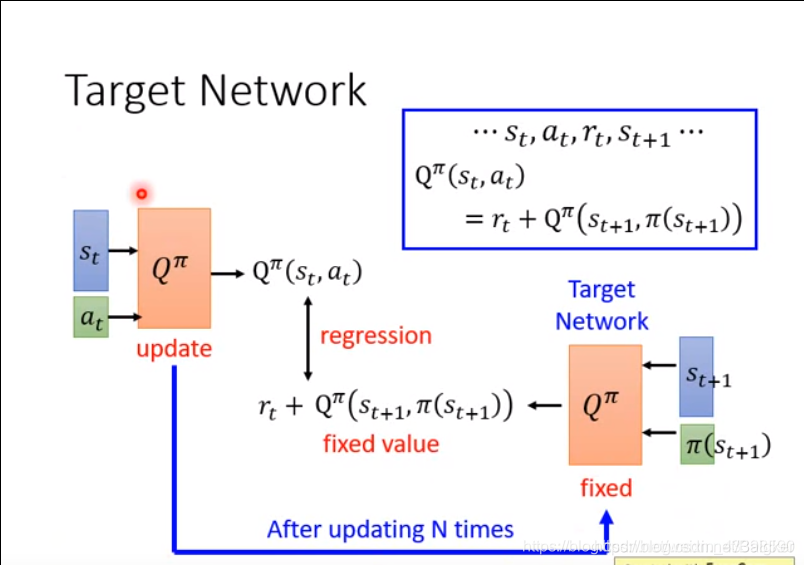
Target Network

我们使用Q-learning的时候，有一个部分$Q^{\pi }(s_t,a_t)=r_t+Q^{\pi }(s_{t+1},\pi (s_{t+1}))$这和之前的TD方法是类似的（同样都有Rewarf值）。
因为我们训练的时候不希望改变我们的Target，因为我们要拟合一个不停变化的值是相当困难的。所以我们选择固定Target的值，不改变他的参数，在这种情况下进行训练。
具体过程如下：

Exploration

没有探索到的位置的$Q$值始终为0，因而一直不会被选中（如果使用的是神经网络这种现象较弱，但是依然存在）。
所以为了避免每次都做出同样的选择，我们可以采用以下的方法：

Replay Buffer

这个方法把最近的与环境交互结果数据（不一定是同一个π \piπ出来的数据）都放到缓存区里，利用这些数据进行训练。但是使用不同的π \piπ值会不会影响我们的训练呢？结论是不会的。

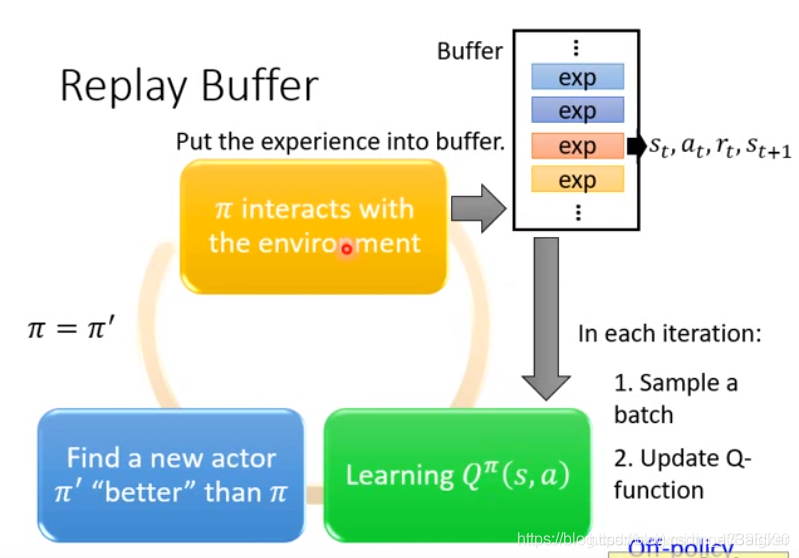
算法执行过程

Q-Learning的Tips

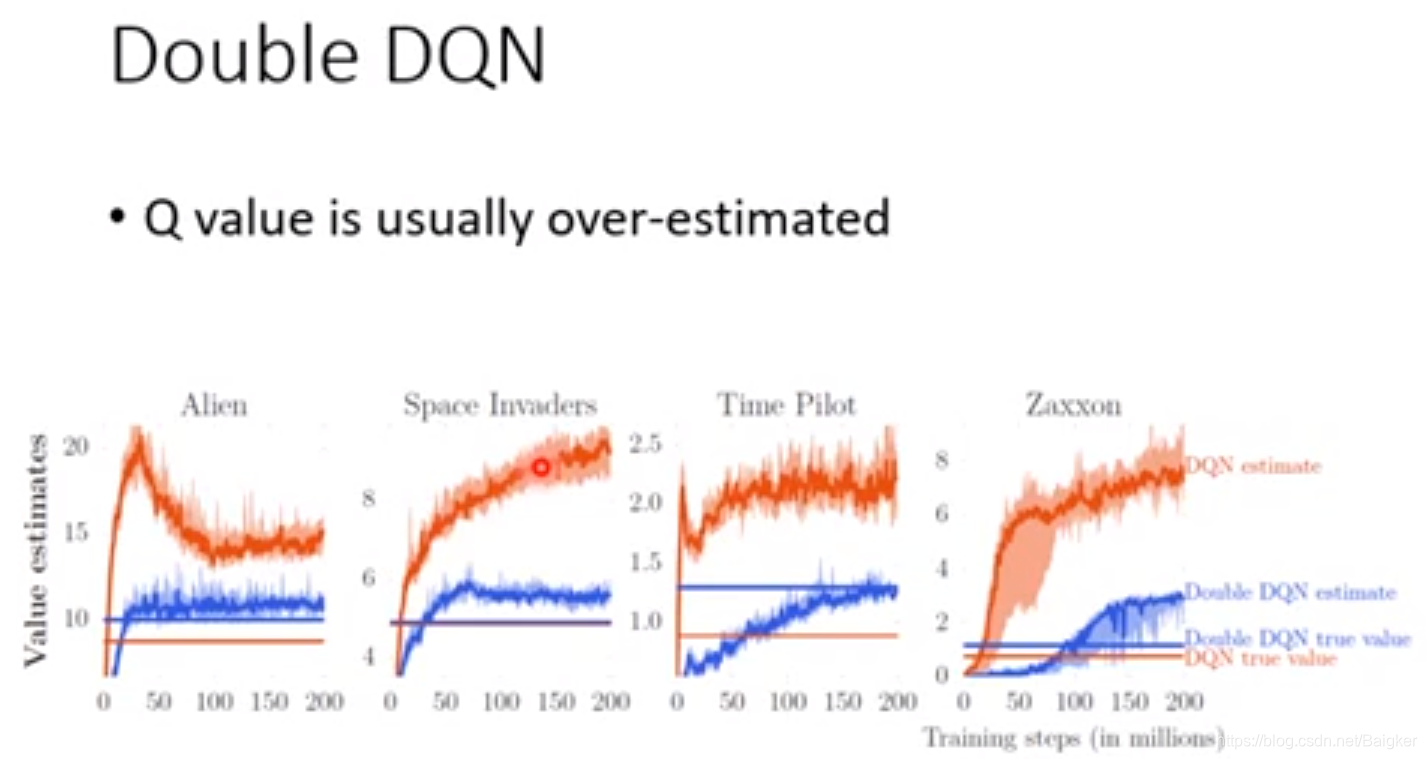
Double DQN

我们发现$Q$总是被高估。（Alien图）
原因在于每次更新Actor时我们都会选择一Reward最大的Action，一旦某个Action被高估了，他就很有可能被选中，从而将这个偏差不断累积下去。


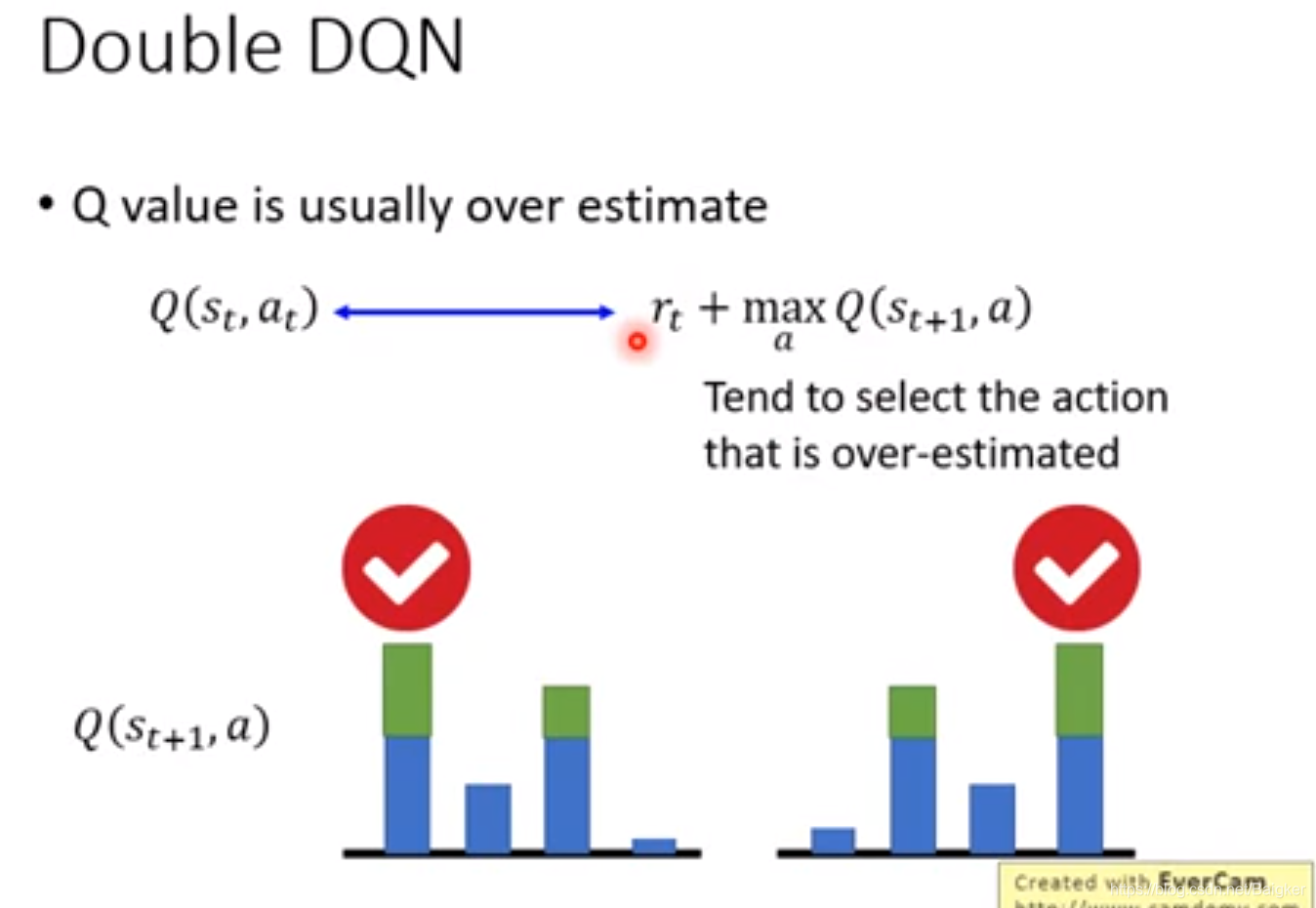
解决方法也很巧妙：用两个$Q$函数，一个负责选Action，一个负责给Reward。这样只有两个函数同时出问题时，最后结果才会被高估。这样高估的概率大大减少了。

Dueling DQN

Dueling DQN不需要太了解，只需要知道他改了原来Network的架构：原来直接输出$Q$，现在把$Q$拆成$V(x)$与$A(s,a)$的和。

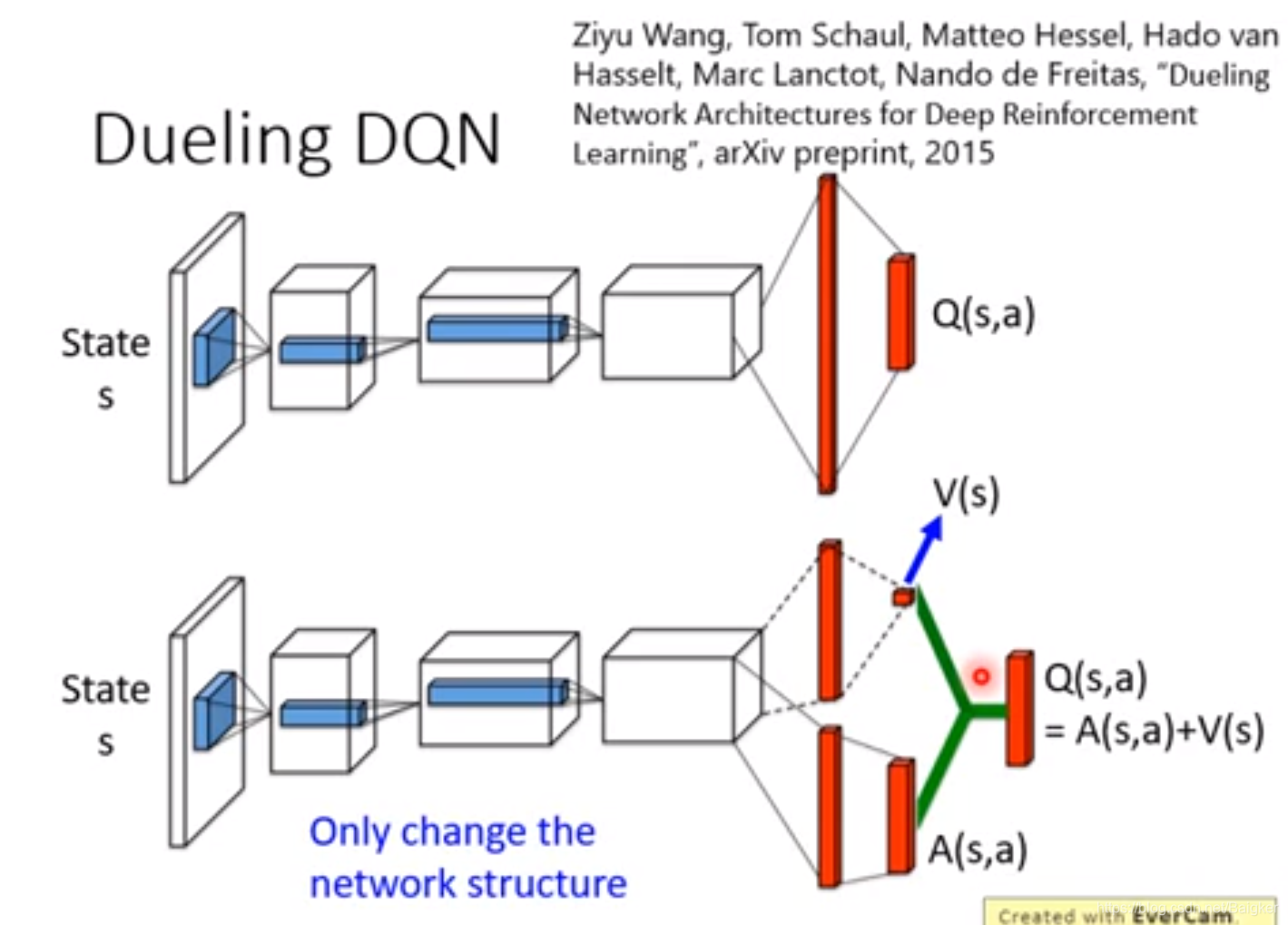
这样的好处是修改数值的时候很方便。
为了防止出问题，我们要让NN尽量改V而不是A。因此要做如下限制。

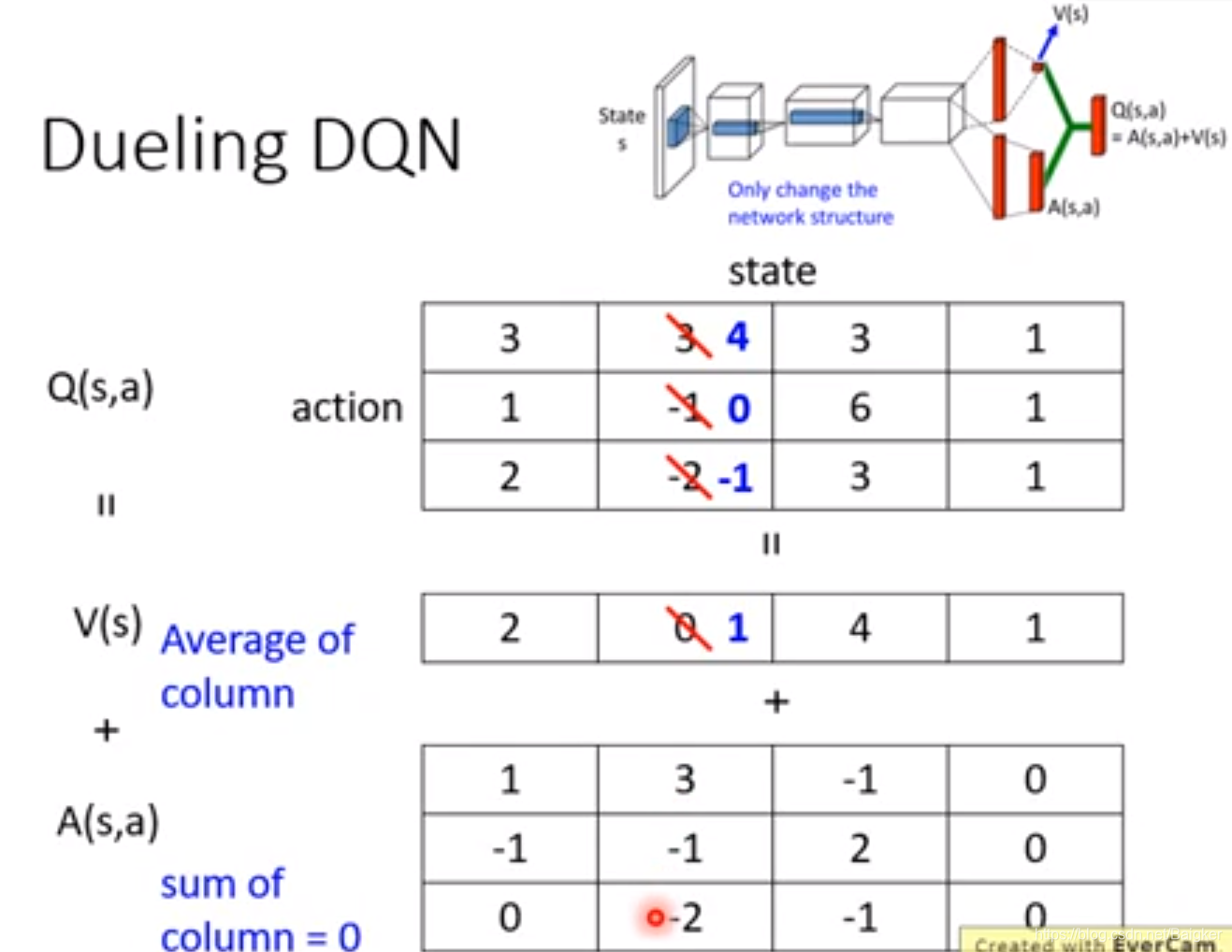
Muti-Step

我们可以平衡一下MC和TD方法。

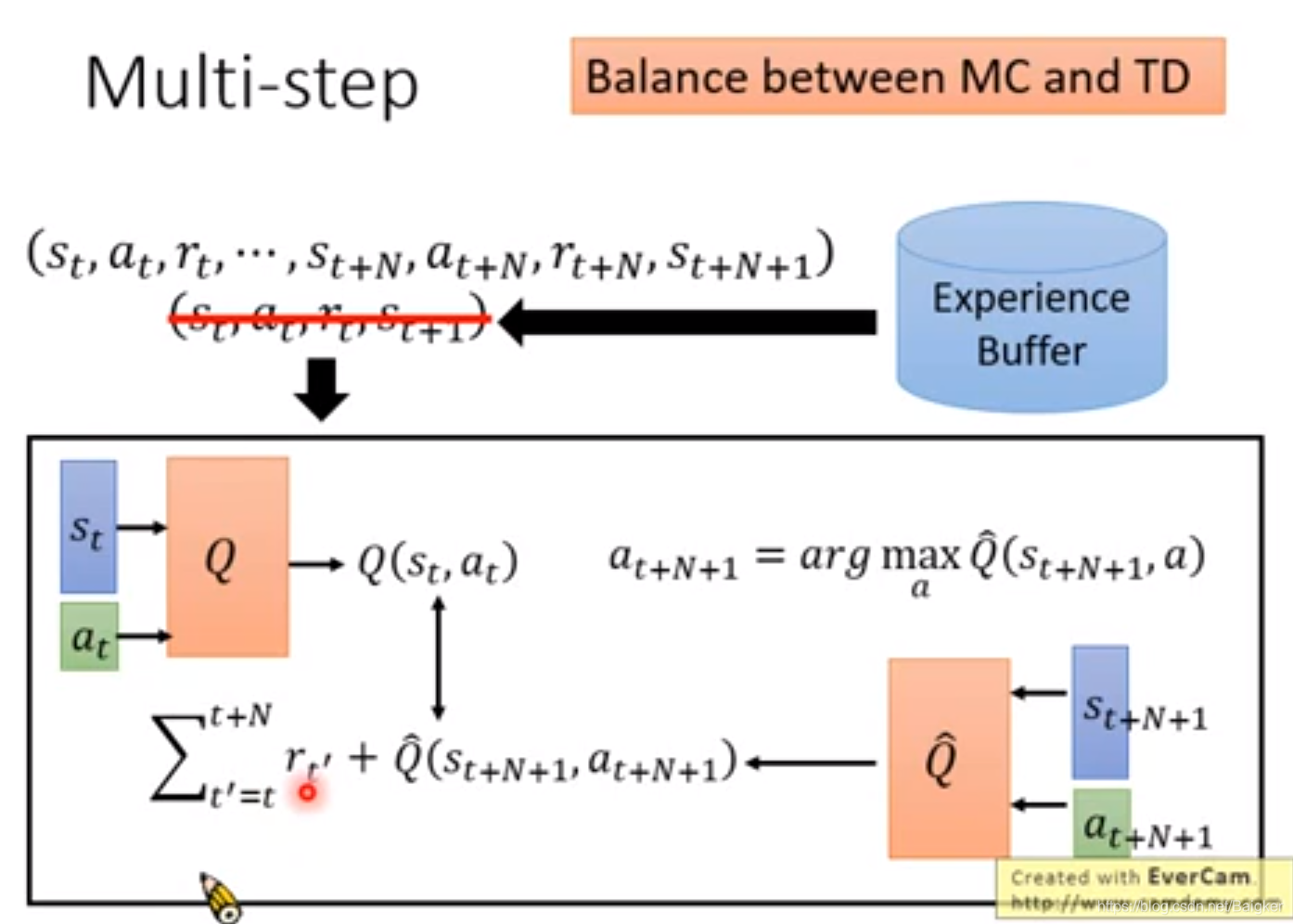
Noisy Net

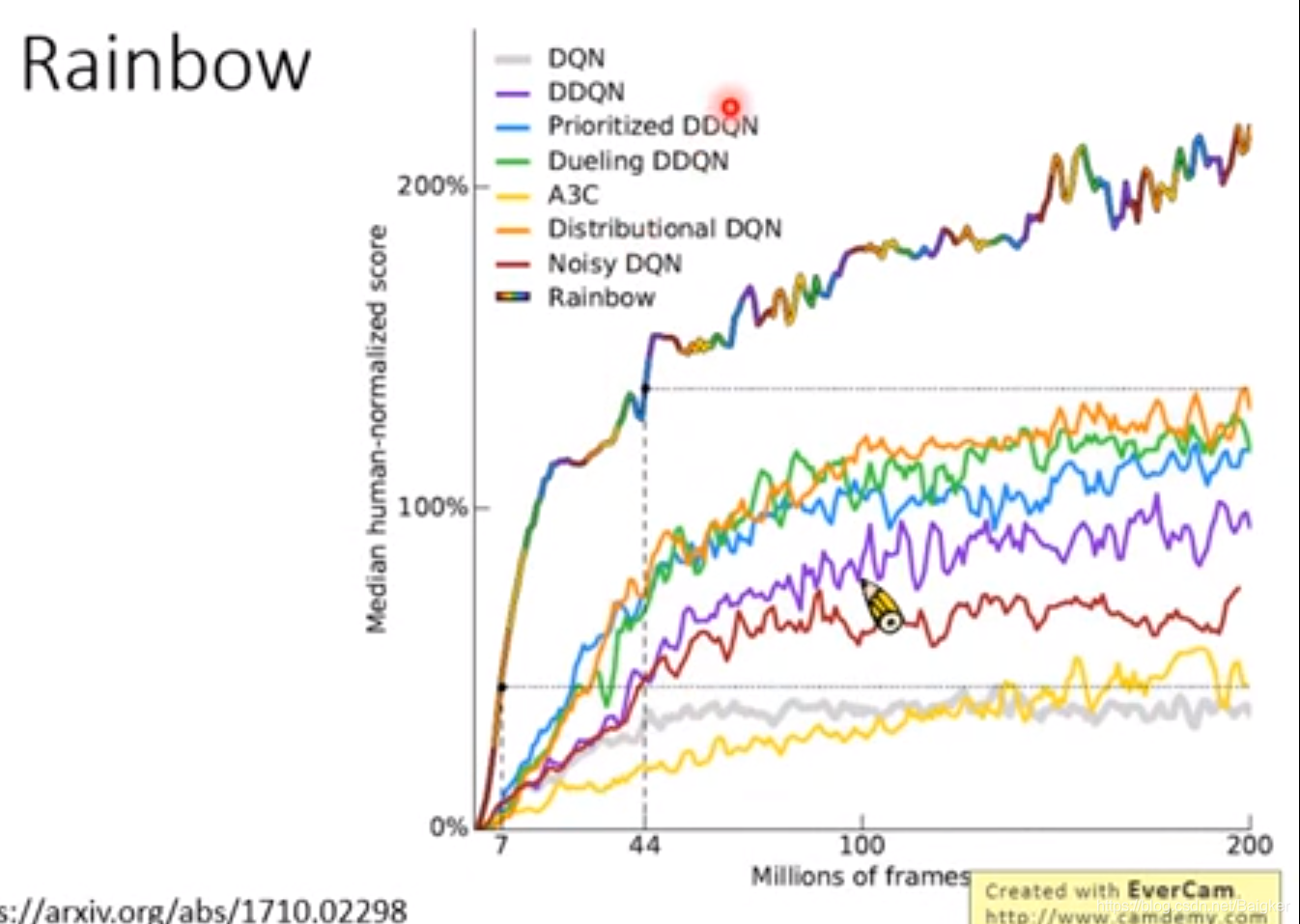
Distributional Q-function

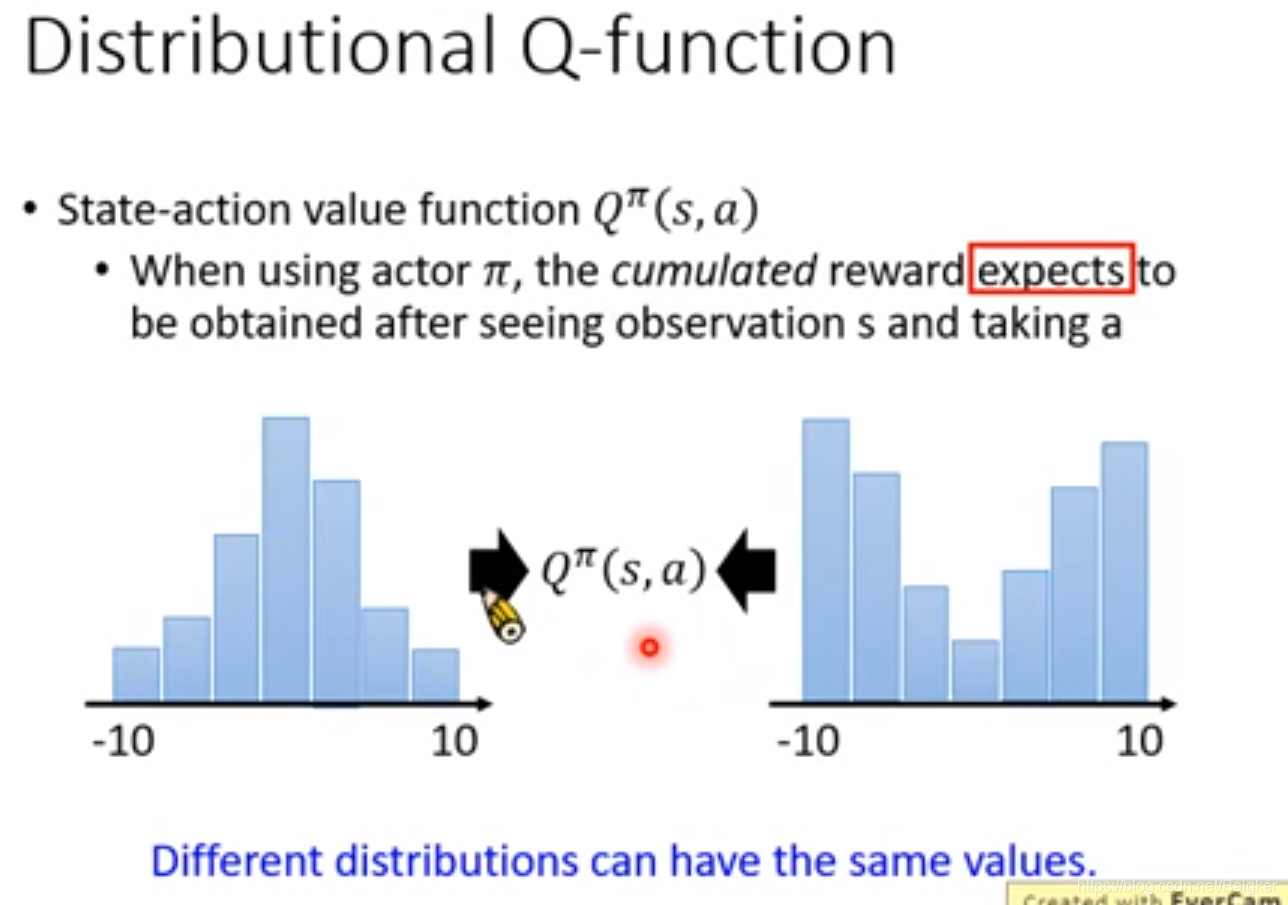
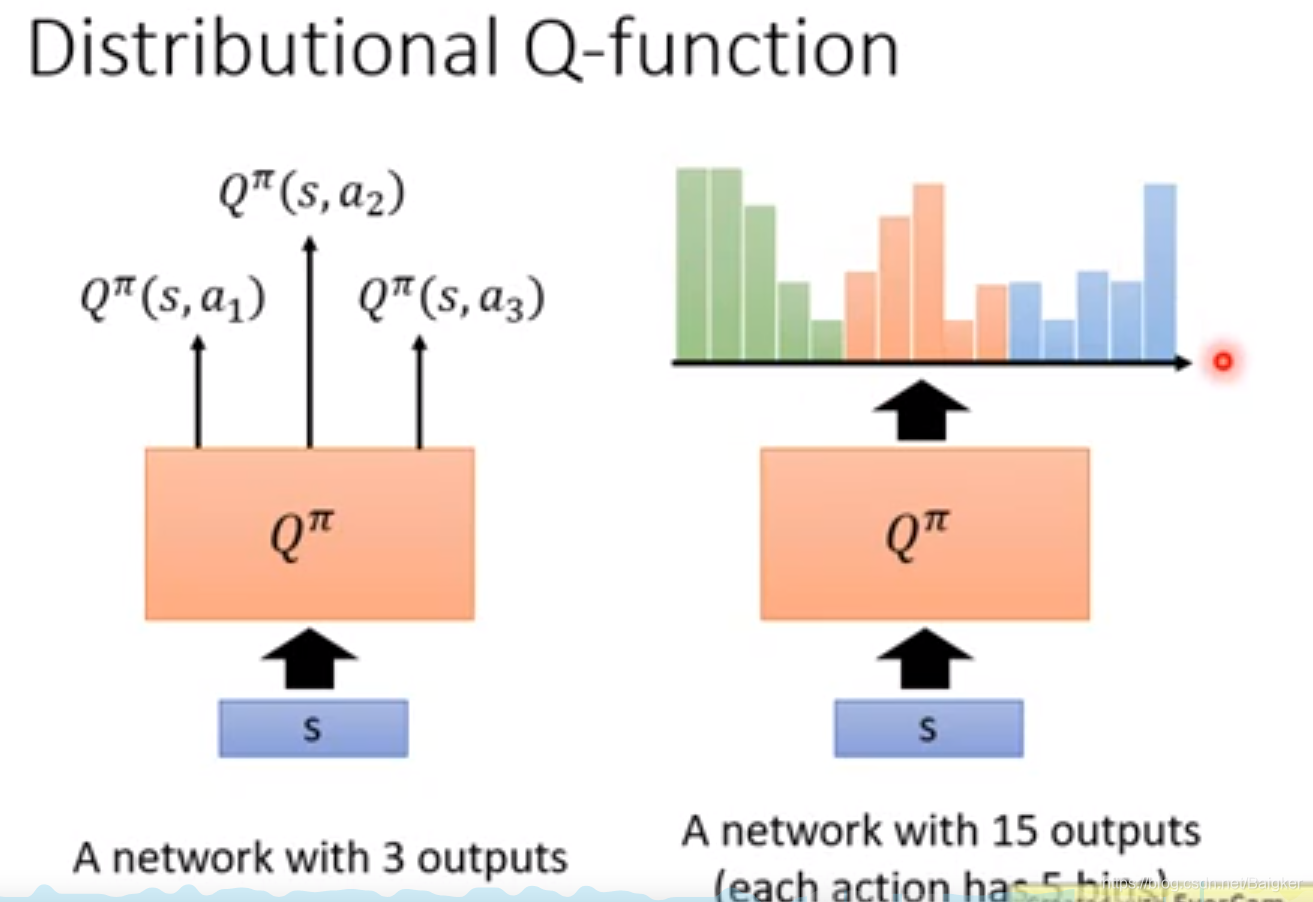
Rainbow

Rainbow就是把这一堆技术全用起来。
个人感觉是瞎搞，用处不大。

连续Q-learning

当动作是一个连续的向量
$a=\arg {\max }_{a}Q(s,a)$
这个式子就不能通过穷举计算得出，所以我们要怎样进行选择呢。
方法一：大力枚举。会丢失精度；
方法二：Gradient Descent。会大幅降低速度。

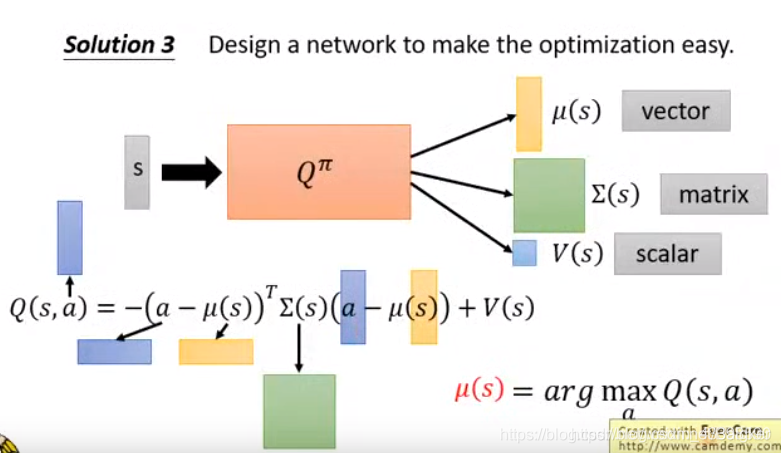
方法三将$Q$拆成一个向量$\mu (s)$、一个矩阵$\Sigma (s)$和一个标量$V(s)$。但实现起来十分复杂。

我们还可以使用别的方法：不用Q-Learning，而是用Actor+Critic。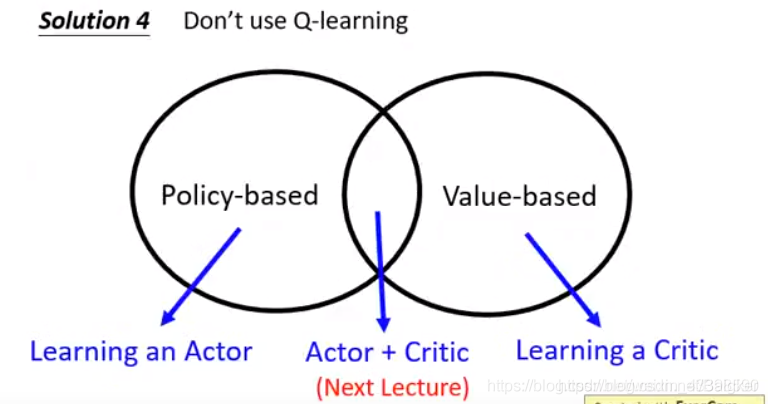

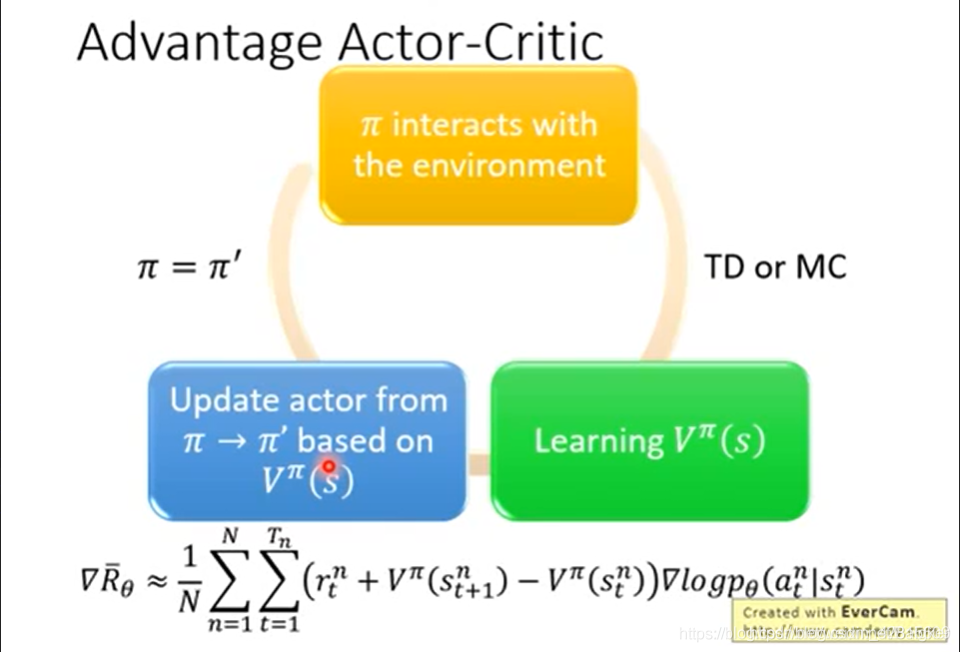
Actor+Critic

Actor+Critic最有名的算法就是A3C。其实A3C实现起来并不难，就是把Policy的公式部分内容用Critic里的函数替代就行了，如下：

但是，这样可能需要训练两个网络。我们做个变换，利用公式$Q_t=E[r_t+V(s_{t+1})]$但是，这样其实引入了一个随机的东西，即$r$。

整个流程如下：用 $\pi$去与环境互动，得到数据，通过 TD 或 MC 的方法，从数据中得到$V$的估值，并且按照上式对$\pi$进行梯度下降。

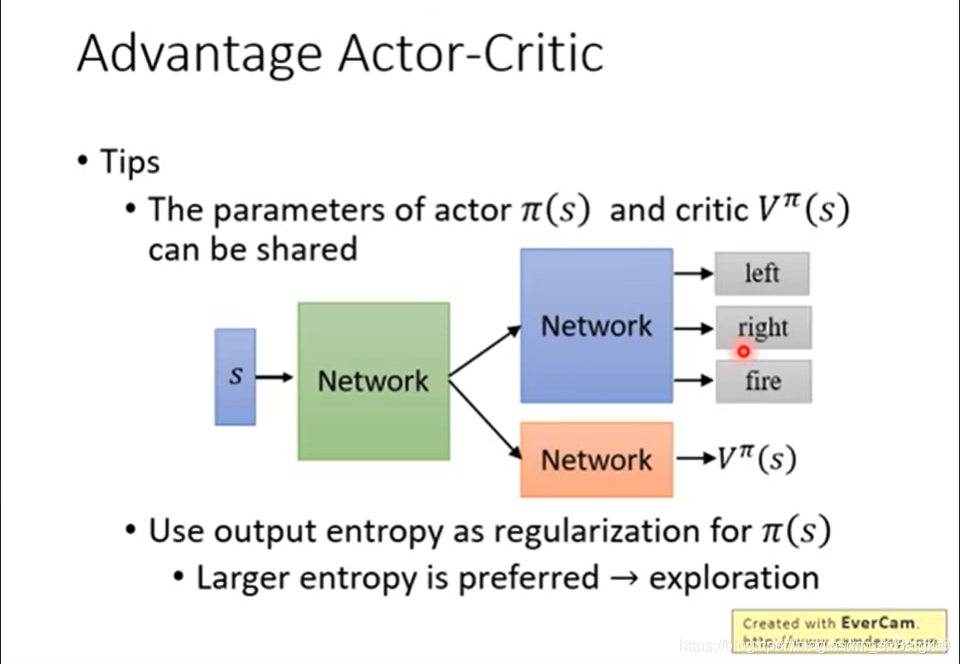
在训练时，可以共享一些参数。此外，还可以对$\pi (s)$做熵值的正则。

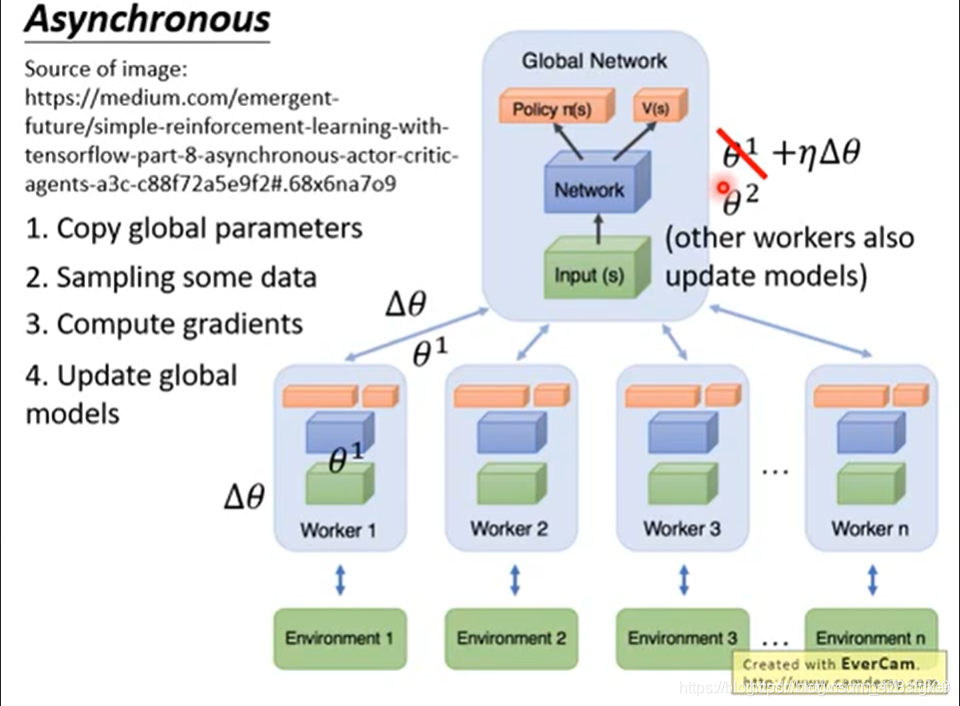
此外，为了提升速度，我们还可以同时开几个 worker （一个 worker 一个 CPU），并行地与环境互动，计算出梯度，传回去。

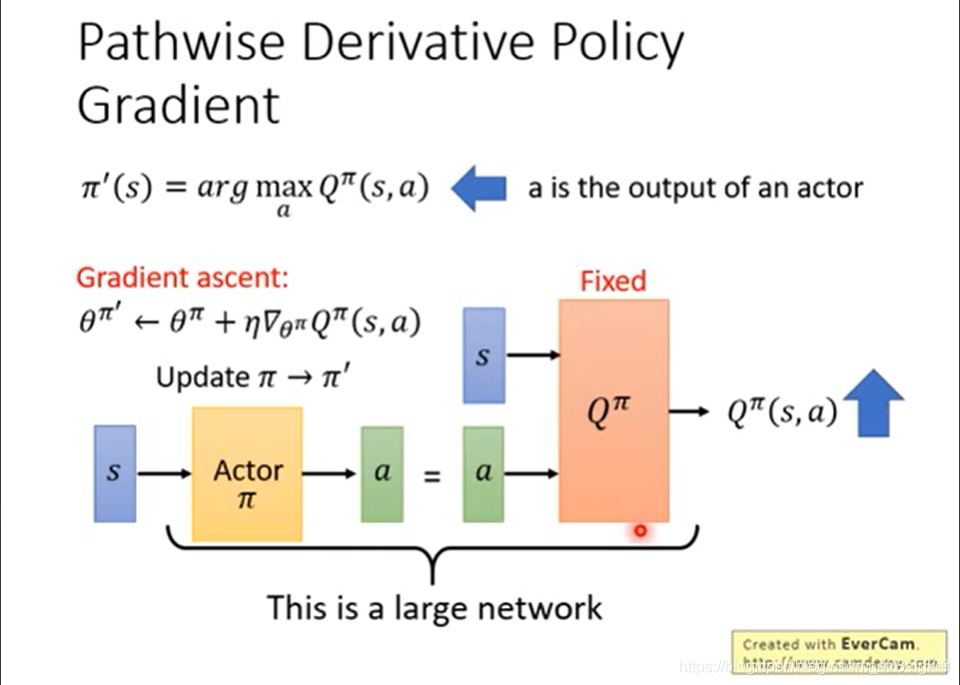
Pathwise derivative policy gradient

传统的Actor-critic只会对State和Action做出评价。
而在 Pathwise derivative policy gradient 中，不但告诉 actor 好坏，还告诉其该怎么做。

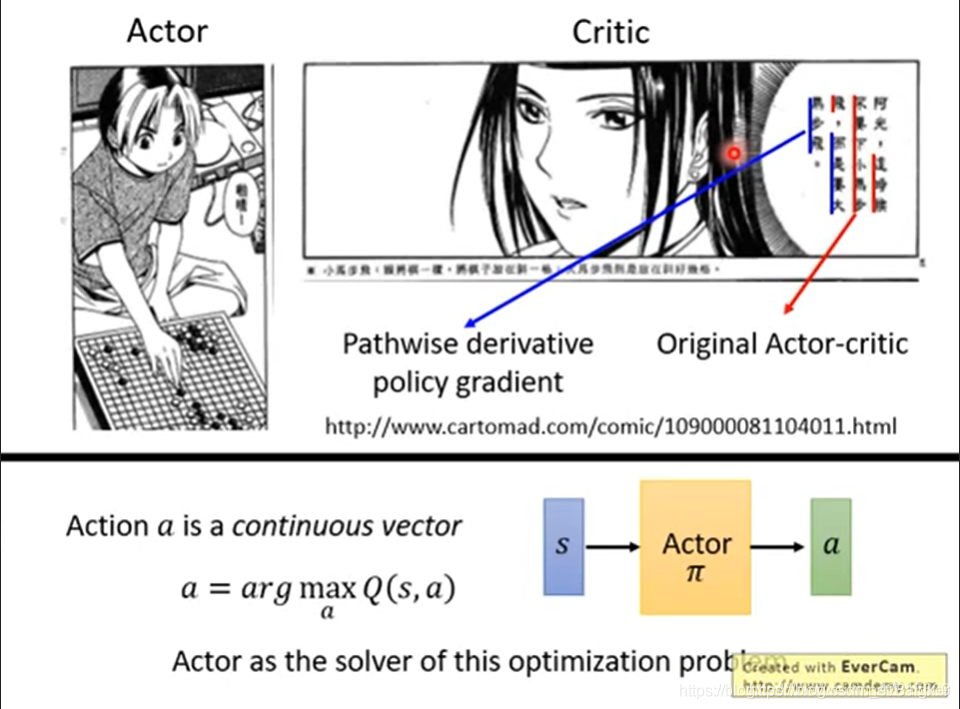
实现中，我们要使用 GAN 的架构。Q 与 Actor 分别训练。在训练 Actor 时，就将 Q 固定住。


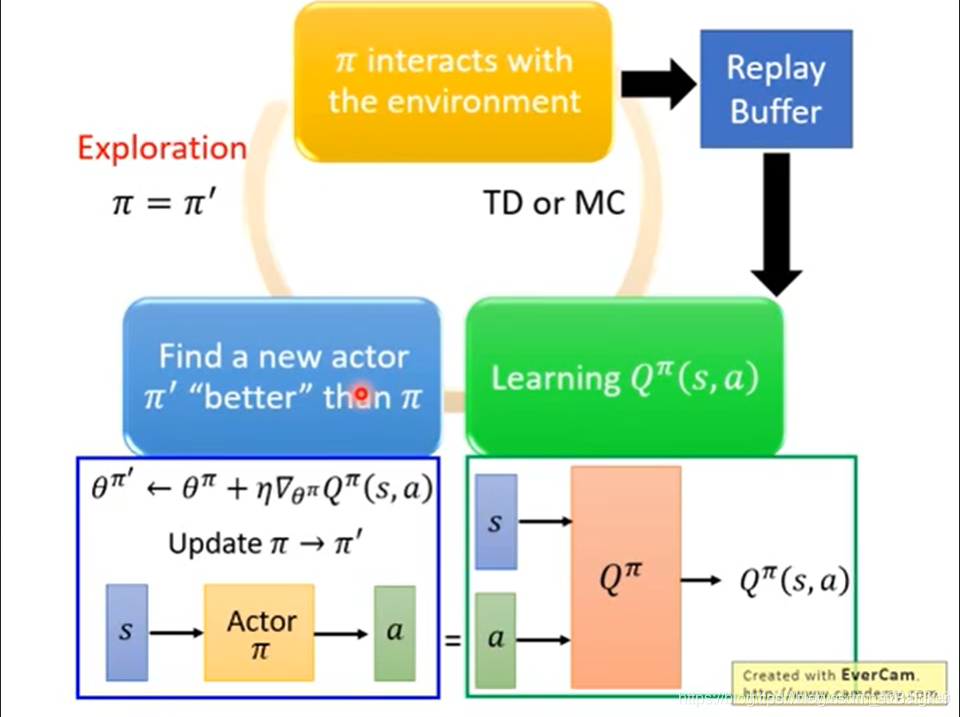
此外，在 Q-Learning 中好用的技巧，这里都可以用到。
如果需要求$a$，直接从$\pi (s)$输出就好。

但是，如上，其与GAN很相似，但是都是很难训练的。