[人工智能]pytorch学习13：实现LetNet和学习nn.Module相关基本操作

用pytorch实现经典的LeNet网络。

网络结构图：

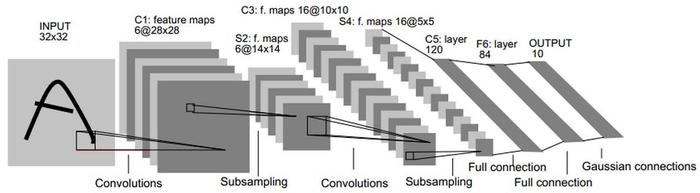
模型建立代码

LeNet包含如下层：

• 二维卷积层$([32,32]\to [6,28,28])$，激活函数$relu$
• 池化层$(\to [6,14,14])$
• 二维卷积层$(\to [16,10,10])$，激活函数$relu$
• 池化层$(\to [16,5,5])$
• 打平向量$(\to [16?5?5])$
• 全连接层$(\to [120])$，激活函数$relu$
• 全连接层$(\to [84])$，激活函数$relu$
• 全连接层$(\to [10])$

import torch
import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        # 1 维输入图像通道，6 维输出通道
        # 卷积核为 5x5 的卷积核
        self.conv1 = nn.Conv2d(1, 6, 5)
        # 6 维输入图像通道，16 维输出通道
        # 卷积核为 5x5 的卷积核
        self.conv2 = nn.Conv2d(6, 16, 5)

        # 最后的三层全连接
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # 用 2x2 的窗口对第一层卷积进行 Max pooling池化操作
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # 对第二层卷积进行同样操作
        # 如果池化窗口形状为正方形，可以只输入一个数
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)

        # 将 x 打平成一维向量
        x = x.view(-1, self.num_flot_features(x))

        # 全连接层的前向传播
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flot_features(self, x):
        """
        计算除批次外的所有维度
        用来确定打平后的维度
        如 x.shape = [100, 28, 28]
        返回值为 28 * 28

        :param x: 数据
        :return: 除第一维外的所有维度之积
        """
        size = x.size()[1:]
        num_features = 1
        for s in size:
            num_features *= s

        return num_features

输出网络结构

可以通过打印对象直接查看构成网络的各层属性。

示例代码：

# 创建LetNet对象
net = Net()
# 输出网络结构
print('网络结构：\n', net)

输出结果：

网络结构：
 Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

查看可训练参数

可以通过 .parameters() 获得各层参数，可用来更新权重。

示例代码：

# 创建LetNet对象
net = Net()

# 使用 net.parameters 可以获得被学习参数的列表和值
params = list(net.parameters())

print('需训练的参数矩阵个数：', len(params))

for p in params:
    print(p.size())

输出结果：

需训练的参数矩阵个数： 10
torch.Size([6, 1, 5, 5]) # 第一层卷积核的参数
torch.Size([6]) # 第一层卷积核的偏置
torch.Size([16, 6, 5, 5]) # 第二层卷积核的参数
torch.Size([16]) # 第二层卷积核的偏置
torch.Size([120, 400]) # 第一次全连接的权重
torch.Size([120]) # 第一层全连接的偏置
torch.Size([84, 120]) # 第二层全连接的权重
torch.Size([84]) # 第二层全连接的偏置
torch.Size([10, 84]) # 第三层全连接的权重
torch.Size([10]) # 第三层全连接的偏置

前向传播

使用 对象名(输入数据)来进行前向计算。

示例代码：

# 创建LetNet对象
net = Net()

# 表示为：有1批数量为1的32*32大小的图片
input_ = torch.randn(1, 1, 32, 32)
out = net(input_)
print('网络输出：', out)

输出结果：

网络输出： tensor([[-0.0573, -0.0214, -0.0619,  0.0998,  0.0441, -0.0282,  0.0089,  0.0991,
         -0.0603, -0.0076]], grad_fn=<AddmmBackward>)

反向传播和梯度下降

可以用过 loss.backward() 来更新梯度，然后用 net.parameters() 来获取并更新参数。

示例代码：

# 创建LetNet对象
net = Net()

# 创建 X
# 表示为：有1批数量为1的32*32大小的图片
x = torch.randn(1, 1, 32, 32)

# 创建 Y
y = torch.randn(1,10)

# 前向计算
y_pred = net(x)

# 设置损失函数为 MSE
loss_func = nn.MSELoss()

# 计算损失
loss = loss_func(y_pred, y)
print('梯度下降前loss:', loss)

# 输出第一层卷积在反向传播前的梯度
print('conv1.bias.gard 反向传播前:', net.conv1.bias.grad)

# 进行反向传播
loss.backward()

# 输出反向传播后的梯度
print('conv1.bias.gard 反向传播后:', net.conv1.bias.grad)

# 更新权重
learning_rate = 1 # 设置学习率为 1，是为了加快权重变化
for p in net.parameters():
	# 更新参数
    # w = w - lr * w_grad
    p.data.sub_(p.grad.data * learning_rate)

# 再次计算结果和损失
y_pred = net(x)
loss = loss_func(y_pred, y)
print('梯度下降后loss:', loss)

输出结果：

梯度下降前loss: tensor(0.7424, grad_fn=<MseLossBackward>)
conv1.bias.gard 反向传播前: None
conv1.bias.gard 反向传播后: tensor([ 0.0236, -0.0085,  0.0035, -0.0035, -0.0115, -0.0085])
梯度下降后loss: tensor(0.0246, grad_fn=<MseLossBackward>)

优化器

若想使用一些经典的优化器来进行权重更新，可在 torch.optim 中快速调用。

通过optimzer = optim.SGD(net.parameters(), lr=1) 的方式绑定参数。然后在反向传播后通过 optimzer.step() 来更新梯度。

示例代码：

import torch.optim as optim

net = Net()

# 设置优化器
optimzer = optim.SGD(net.parameters(), lr=1)

# 计算梯度
x = torch.randn(1, 1, 32, 32)
y = torch.randn(1,10)
y_pred = net(x)
loss_func = nn.MSELoss()
loss = loss_func(y_pred, y)
print('梯度下降前loss:', loss)
loss.backward()

# 更新梯度
optimzer.step()

# 再次预测
y_pred = net(x)
loss = loss_func(y_pred, y)
print('梯度下降后loss:', loss)

输出结果：

梯度下降前loss: tensor(1.0159, grad_fn=<MseLossBackward>)
梯度下降后loss: tensor(0.0834, grad_fn=<MseLossBackward>)

关于 zero_grad

.zero_gard() 用来清理累计的梯度，可以使用形如 net.zero_gard() 或 optimzer.zero_gard() 的代码来使用。但由于上面代码都只进行了一次梯度下降，且经过尝试发现删除有关 .zero_gard() 的代码并不会产生什么影响。为了让自己对 pytorch 的理解更透彻，删除了可能没有对结果产生影响的代码。当在后续学习中，出现此代码必不可少的情况时，再对其功能进行学习研究。