本文是学习《学习OpenCV3》这本书时做的相关总结,主要是记录学习笔记。
一、Point类
P
o
i
n
t
Point
Point类可以用于创建二维点和三维点(例如
c
v
:
:
P
o
i
n
t
2
i
、
c
v
:
:
P
o
i
n
t
3
i
cv::Point2i、cv::Point3i
cv::Point2i、cv::Point3i等)。创建对象时是通过别名来创建的。Point类的别名有:
c
v
:
:
P
o
i
n
t
2
i
、
c
v
:
:
P
o
i
n
t
2
f
、
c
v
:
:
P
o
i
n
t
2
d
、
c
v
:
:
P
o
i
n
t
2
l
、
c
v
:
:
P
o
i
n
t
3
i
、
c
v
:
:
P
o
i
n
t
3
d
、
c
v
:
:
P
o
i
n
t
3
f
cv::Point2i、cv::Point2f、cv::Point2d、cv::Point2l、cv::Point3i、cv::Point3d、cv::Point3f
cv::Point2i、cv::Point2f、cv::Point2d、cv::Point2l、cv::Point3i、cv::Point3d、cv::Point3f。Point类的声明可以是下列形式的任何一种:
c
v
:
:
P
o
i
n
t
{
2
,
3
}
{
i
,
f
,
d
}
cv::Point\{2, 3\}\{i, f, d\}
cv::Point{2,3}{i,f,d}
注释:上面最后的字幕分别表示——
i
=
i
n
t
,
f
=
f
l
o
a
t
,
d
=
d
o
u
b
l
e
i=int, f=float, d=double
i=int,f=float,d=double。
1.1 Point对象的创建方式
方式一:通过默认构造函数创建
cv::Point3f p; //创建float型三维点p并将其初始化为(0,0,0)
方式二:通过复制构造函数创建
cv::Point2i p1; //创建整数二维点并将其初始化为(0,0)
cv::Point2i p2(p1);
方式三:通过值构造
cv::Point2d p3;
p3 = cv::Point2d(2, 3);
cout << p3.x << "; " << p3.y << endl;
cv::Point3f p4(1, 2, 3);
cout << p4.x << "; " << p4.y << "; " << p4.z << endl;
1.2 将Point对象转化为固定向量类
cv::Point3f p5(2,3,5);
cv::Vec3f vec3f = (cv::Vec3f)p5;
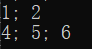
cout << vec3f[0] << "; " << vec3f[1] << "; " << vec3f[2] << endl;
程序运行结果为:

1.3 Point对象中的成员访问方式
cv::Point2i p6(1, 2);
cout << p6.x << "; " << p6.y << endl;
cv::Point3i p7(4, 5, 6);
cout << p7.x << "; " << p7.y << "; " << p7.z << endl;
程序的运行结果:
1.4 Point对象点乘
两个Point对象: P 1 = P o i n t 2 i ( x 0 , x 1 ) P_1=Point2i(x_0, x_1) P1?=Point2i(x0?,x1?), P 2 = P o i n t ( x 2 , x 3 ) P_2=Point(x_2,x_3) P2?=Point(x2?,x3?)
点乘的结果: P 1 ? P 2 = x 0 ? x 2 + x 1 ? x 3 P_1 \cdot P_2 = x_0*x_2+x_1*x_3 P1??P2?=x0??x2?+x1??x3?
cv::Point2f p8(1, 2);
cv::Point2f p9(3, 4);
float val = p8.dot(p9);
cout << val << endl;
cv::Point3f p10(1, 2, 3);
cv::Point3f p11(4, 5, 6);
float val1 = p10.dot(p11);
cout << val1 << endl;
程序运行的结果为:
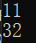
1.5 Point对象叉乘
对叉乘要分两种情况:二维点和三维点。
对于二维点:
两个Point对象:
P
1
=
P
o
i
n
t
2
i
(
x
1
,
y
1
)
P_1=Point2i(x_1, y_1)
P1?=Point2i(x1?,y1?),
P
2
=
P
o
i
n
t
(
x
2
,
y
2
)
P_2=Point(x_2,y_2)
P2?=Point(x2?,y2?)
叉乘的结果:
P
1
×
P
2
=
x
1
?
y
2
?
y
1
?
x
2
P_1 \times P_2=x_1*y_2-y_1*x_2
P1?×P2?=x1??y2??y1??x2?
对于三维点:
两个点对象:
P
1
=
P
o
i
n
t
3
i
(
x
1
,
y
1
,
z
1
)
P_1 = Point3i(x_1,y_1,z_1)
P1?=Point3i(x1?,y1?,z1?),
P
2
=
P
o
i
n
t
3
i
(
x
2
,
y
2
,
z
2
)
P_2 = Point3i(x_2,y_2,z_2)
P2?=Point3i(x2?,y2?,z2?)
叉乘的结果:
P
1
×
P
2
=
(
y
1
?
z
2
?
z
1
?
y
2
,
z
1
?
x
2
?
x
1
?
z
2
,
x
1
?
y
2
?
y
1
?
x
2
)
P_1 \times P_2 = (y_1*z_2-z_1*y_2, z_1*x_2-x_1*z_2, x_1*y_2-y_1*x_2)
P1?×P2?=(y1??z2??z1??y2?,z1??x2??x1??z2?,x1??y2??y1??x2?)
cv::Point2f p8(1, 2);
cv::Point2f p9(3, 4);
cout << p8.cross(p9) << endl;
cv::Point3f p10(1, 2, 3);
cv::Point3f p11(4, 5, 6);
cout << p10.cross(p11) << endl;
程序的输出结果为:

1.6判断点是否在矩形内
注意:该方法只能用于二维点类。
cv::Point2i p12(2, 3);
cv::Rect2i rect(1, 1, 5, 4);
if (p12.inside(rect))
{
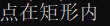
cout << "点在矩形内" << endl;
}
else
{
cout << "点不在矩形内" << endl;
}
程序的输出结果为:
二、Scalar类
Scalar其实是一个四维向量类。Scalar对象中的每一个元素都是双精度浮点数。
2.1 Scalar对象的创建方式
方式一:通过默认构造函数创建
cv::Scalar s; //创建Scalar对象并将对象中的值初始化为0
cout << s[0] << "; " << s[1] << "; " << s[2] << "; " << s[3] << endl;
方式二:通过复制构造函数创建
cv::Scalar s;
cout << s[0] << "; " << s[1] << "; " << s[2] << "; " << s[3] << endl;
cv::Scalar s1(s); //复制构造
cout << s1[0] << "; " << s1[1] << "; " << s1[2] << "; " << s1[3] << endl;
方式三:通过值构造函数创建对象
cv::Scalar s2(5);
cout << s2[0] << "; " << s2[1] << "; " << s2[2] << "; " << s2[3] << endl;
cv::Scalar s3(2, 5, 6, 9);
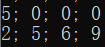
cout << s3[0] << "; " << s3[1] << "; " << s3[2] << "; " << s3[3] << endl;
程序输出结果为:
2.2真值测试
真值测试是测试Scalar对象的后三个值是否等于0,如果等于零就返回真,否则返回假。
cv::Scalar s4(2, 5, 6, 9); //如果 s4[1]==s4[2]==s4[3]==0,则返回真
cv::Scalar s5(2, 0, 0, 0);
cout << s4.isReal() << endl;
cout << s5.isReal() << endl;
程序输出结果为:
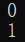
2.3两个Scalar对象相乘
两个Scalar对象相乘,是元素对应位置相称。返回的任然是Scalar对象。
cv::Scalar s6(1, 2, 3, 4);
cv::Scalar s7(5, 6, 7, 8);
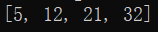
cout << " " << s6.mul(s7) << endl;
程序运行结果:
三、Size类
Size类包含两个数据成员,分别是width和height。opencv中Size类的别名分别有:cv::Size、cv::Size2d、cv::Size2f、cv::Size2i、cv::Size2l。
3.1Size对象的创建方式
方式一:通过默认构造函数创建
cv::Size2d s2; //构造Size对象并将其成员初始化为0
cout << s2.width << "; " << s2.height << endl;
方式二:通过复制构造函数创建
cv::Size2d s2;
cout << s2.width << "; " << s2.height << endl;
cv::Size2d s3(s2); //复制构造
方式三:通过值构造函数创建对象
cv::Size2i s4(2, 3); //值构造
cout << s4.width << "; " << s4.height << endl;
程序的输出结果为:

3.2求size对象的面积
cv::Size2i s4(2, 3);
cout << s4.width << "; " << s4.height << endl;
cout << s4.area() << endl;
程序的输出结果为:

四、Rect类
Rect对象是一个平行于坐标轴的矩形,Rect对象包含四个成员分别是:x、y、width、height。x、y代表矩阵左上角的点,width、height代表矩形的宽高。opencv中Rect类的别名有:cv::Rect、cv::Rect2d、cv::Rect2f、cv::Rect2i。
4.1Rect对象的构造方式
方式一:默认构造函数构造
cv::Rect r1; //使用默认构造函数构造并将x、y、width、height初始化为0
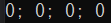
cout << r1.x << "; " << r1.y << "; " << r1.width << "; " << r1.height << endl;
程序输出结果为:
方式二:复制构造函数构造
cv::Rect r1;
cout << r1.x << "; " << r1.y << "; " << r1.width << "; " << r1.height << endl;
cv::Rect r2(r1); //调用复制构造函数
方式三:值构造
cv::Rect r3(1, 2, 3, 4);
cv::Rect r4 = cv::Rect(1, 2, 3, 4);
方式四:由左上点Point和宽高Size构造
cv::Point p1(4, 5);
cv::Size size1(7, 8);
cv::Rect r4(p1, size1);
cv::Rect(p1, size1);
方式五:由左上点和右下点构造
cv::Point p2(5, 6);
cv::Point p3(8, 9);
cv::Rect r5 = cv::Rect(p2, p3);
cv::Rect r6(p2, p3);
4.2Rect对象支持的相关操作
| 操作方法 | 描述 |
|---|---|
| rect.x、rect.y、rect.width、rect.height | 访问rect对象中的成员 |
| rect.area() | 计算矩形rect的面积 |
| rect.contains(point) | 判断点point是否在矩形内 |
| rect.tl() | 获取矩形的左上点 |
| rect.br() | 获取矩形的右下点 |
4.3矩形的计算
4.3.1两个矩形的交集
cv::Rect r1(1, 2, 20, 30);
cv::Rect r2(8, 9, 20, 30);
cv::Rect r3 = r1 & r2; //
4.3.2同时包含两个矩形的最小外接矩形
cv::Rect r1(1, 2, 20, 30);
cv::Rect r2(8, 9, 20, 30);
cv::Rect r3 = r1 | r2;
4.3.3平移矩形
cv::Rect r3(1, 2, 3, 4);
cv::Point2i p(2, 3);
cv::Rect r7 = r3 + p; //行方向平移2,列方向平移3
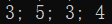
cout << r7.x << "; " << r7.y << "; " << r7.width << "; " << r7.height << endl;
程序运行结果为:
4.3.4改变矩形的宽高
cv::Rect r3(1, 2, 3, 4);
cv::Size2i sz(4, 5);
cv::Rect r8 = r3 + sz; //将矩形的宽增加3、矩形的高增加4
cout << " " << r8.x << "; " << r8.y << "; " << r8.width << "; " << r8.height << endl;
程序运行结果为:

4.3.5判断两个矩形是否相等
cv::Rect r1 = cv::Rect(1,2,3,4)
cv::Rect r2(1,2,5,6)
bool eq = (r1 == r2)
bool eq1 = (r1 != r2)
五、RotatedRect类
RotateRect类是旋转矩形类,该类包含三个成员变量分别是:中心cv::Point2f、矩形大小cv::Size2f、以及角度float。
5.1RotateRect对象的构造方式
方式一:默认构造函数构造
cv::RotatedRect rr; //使用默认构造函数构造对象,并将其成员变量初始化为0
cout << " " << rr.size << "; " << rr.center << "; " << rr.angle << endl;
方式二:采用复制构造函数构造
cv::RotatedRect rr;
cout << " " << rr.size << "; " << rr.center << "; " << rr.angle << endl;
cv::RotatedRect rr1(rr); //复制构造
cout << " " << rr1.size << "; " << rr1.center << "; " << rr1.angle << endl;
方式三:值构造
cv::Point2f p1(2, 3);
cv::Size2f sz1(4, 5);
float angle = (60 * 3.14159 / 180);
cv::RotatedRect rr2(p1, sz1, angle); //值构造
cout << " " << rr2.size << "; " << rr2.center << "; " << rr2.angle << endl;
5.2RotatedRect对象的相关操作
5.2.1访问对象的成员
cv::RotatedRect rr;
cout << " " << rr.size << "; " << rr.center << "; " << rr.angle << endl;
5.2.2获取矩形的四个顶点
cv::Point2f p1(2, 3);
cv::Size2f sz1(4, 5);
float angle = (60 * 3.14159 / 180);
cv::RotatedRect rr2(p1, sz1, angle);
cout << " " << rr2.size << "; " << rr2.center << "; " << rr2.angle << endl;
cv::Point2f points[4];
rr2.points(points); //获取矩阵rr2的四个顶点
for (int i = 0; i < sizeof(points) / sizeof(cv::Point2f); i++)
{
cout << points[i] << endl;
}
六、固定矩阵
固定矩阵是在创建时就已经知道其维度的矩阵。固定矩阵别名的基本构建格式为:Matx{1,2,3,4,5,6}{1,2,3,4,5,6}{d,f}。也可以通过模板自己构建(如cv::Matx<7,7,float>)。
6.1固定矩阵的构造方式
方式一:默认构造函数构造
cv::Matx23f m23f; //创建2行3列的矩阵。默认构造函数构造对象,并初始化为0
cout << " " << m23f << endl;
方式二:复制构造函数构造
cv::Matx33d m33d;
cv::Matx33d m33d_1(m33d); //复制构造函数创建
方式三:值构造
cv::Matx21f m21f(2, 3); //值构造,创建2X1的矩阵
6.2Matx类支持的操作
| 操作示例 | 说明 |
|---|---|
| mat1.dot(mat2) | 两个矩阵的对应元素相乘并相加,返回值与矩阵中元素类型相同 |
| mat1.ddot(mat2) | 两个矩阵的对应元素相乘并相加,返回值为double型 |
| mat1.reshape<m,n> | 改变矩阵的形状,mat1.cols ? * ? mat1.rows 等于m ? * ? n |
| a ? m a t 1 a * mat1 a?mat1 | 数乘矩阵,数乘以矩阵中的每个元素 |
| m a t 1 ( i , j ) mat1(i,j) mat1(i,j) | 访问矩阵中的 i , j i,j i,j元 |
| m a t 1 = = m a t 2 mat1 == mat2 mat1==mat2 | 判断两个矩阵是否相等 |
| m a t 1. g e t _ m i n o r < m , n > ( i , j ) mat1.get\_minor<m,n>(i,j) mat1.get_minor<m,n>(i,j) | 从矩阵 m a t 1 mat1 mat1中提取 ( i , j ) (i,j) (i,j)处的 m ? n m * n m?n的子矩阵 |
| m a t 1. r o w ( i ) mat1.row(i) mat1.row(i) | 提取矩阵 m a t 1 mat1 mat1的第 i i i行 |
| m a t 1. c o l ( j ) mat1.col(j) mat1.col(j) | 提取矩阵 m a t 1 mat1 mat1的第 j j j列 |
| m a t 1. t ( ) mat1.t() mat1.t() | 计算 m a t 1 mat1 mat1的转置 |
七、固定向量类
固定向量类是在定义时就确定了向量长度的向量。固定向量类的别名构成方式为: c v : : V e c { 2 , 3 , 4 , 5 , 6 } { b , s , w , i , f , d } cv::Vec\{2,3,4,5,6\}\{b,s,w,i,f,d\} cv::Vec{2,3,4,5,6}{b,s,w,i,f,d}。
7.1固定向量的构造方式
方式1:默认构造方式构造
Vec3d vec3d;
方式2:复制构造函数构造
Vec3d vec3d;
Vec3d vec3d1(vec3d); //复制构造函数
方式3:值构造
Vec4f vec4f(1, 2, 3, 4); //值构造