本文为参考教程 DEEP LEARNING WITH PYTORCH: A 60 MINUTE BLITZ的学习笔记,只做简单记录方便学习,完整版请参照原文。
上半部分传送门:[pytorch入门]——1小时学习笔记(上)
3.3 神经网络搭建
(1) 待搭建的卷积网络介绍
介绍一下待搭建的卷积神经网络
- 输入单通道的32x32图片。
先经过6个5x5x3维的 filter(过滤器)/kernel(卷积核),步长step=1,填充padding=0,得到28x28x10的输出,(n+2p-f)/s+1 = 32-5+1=28 。经过ReLu激活函数,传递到下一层。 - 再通过最大池化层,池化层边长f = 2,步长 = 2,可以把输入的长和宽缩小一半,通道数保持不变。结构变为14x14x6。
- 经过16个10x10的卷积核,f = 5 , s = 1, 维度变为10x10x16*(14-5)/1+1=10* 同理使用ReLu激活,传递到下一层。
- 第二个池化层,维度变为5x5x16。
- 将5x5x16一维展开为一个向量。
- 第一个全连接层FC1,维度变为120
- 第二个全连接层FC2,维度变为84
- 第三个全连接层FC3,维度变为10
结构如下图所示,为
**CONV1 - POOL1 - CONV2 - POOL2 - FC1 - FC2 - FC3 **
具体为
input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
-> flatten -> linear -> relu -> linear -> relu -> linear
-> MSELoss
-> loss
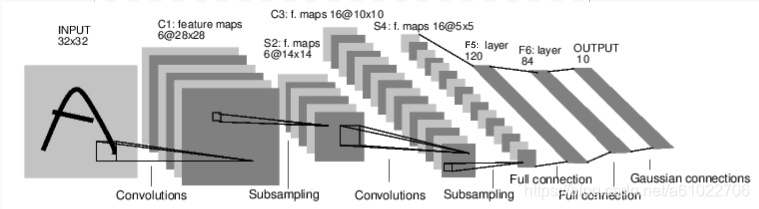
下面这张图来自吴恩达课程中的卷积神经网络的举例,几乎和上图一致,只不过最开始的图片输入是三通道的,最后的softmax也依然是一个全连接层。

神经网络训练过程可以概括为:
①定义网络结构和待学习的参数
② 遍历数据集,将其输入到网络当中
③计算loss损失(输出与真实值之间的差距)
④计算梯度,将梯度传播回网络的参数中
⑤使用梯度下降法来更新参数,更新公式通常为 weight = weight - learning_rate*gradient
(2)开始网络搭建
1.基于torch.nn包来定义网络结构
import torch
import torch.nn as nn
import torch.nn.functional as F
#搭建的网络继承了nn.Moudule,这是一个神经网络的组件,封装了一些参数和功能
class Net(nn.Module):
def __init__(self):
super(Net,self).__init__()
#kernel 定义两个卷积层, nn.Conv2d是二维卷积,是对具备长x宽的输入进行卷积。参数分别是输入的channel,输出的channel,卷积核的边长
self.conv1 = nn.Conv2d(1,6,5)
self.conv2 = nn.Conv2d(6,16,5)
#全连接层 进行y=Wx+b的操作,nn.Linear对应输入的维度和输出的维度
self.fc1 = nn.Linear(16*5*5,120)
self.fc2 = nn.Linear(120,84)
self.fc3 = nn.Linear(84,10)
#定义前向传播
def forward(self,x):
#x先经过conv1,再relu激活,再最大池化
x = F.max_pool2d(F.relu(self.conv1(x),(2,2))
#传递到下一层继续。pooling的size若是一个平方数的话,最后的参数可以只写单独的一个数字
x = F.max_pool2d(F.relu(self.conv1(x),2))
x = torch.flatten(x,1)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
#初始化
net = Net()
print(net)
output
Net(
(conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
(conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(fc1): Linear(in_features=400, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=84, bias=True)
(fc3): Linear(in_features=84, out_features=10, bias=True)
)
我们定义了前向传播的函数,而反向传播的函数会自动自动生产,而不需要写。
可以通过net.parameters()来查看模型的参数。
下面随机初始化一个输入,并查看通过前向传播后的输出
input = torch.randn(1,1,32,32)
out = net(input)
print(out)
out:
tensor([[-0.0794, 0.0241, 0.0712, -0.0940, 0.0481, -0.0220, 0.0628, 0.0115,
-0.0880, -0.0059]], grad_fn=<AddmmBackward>)
用随机梯度将所有参数的梯度缓冲置零
net.zero_grad()
out.backward(torch.randn(1, 10))
(3)定义Loss Function
Loss Function用来计算输出与真实值之间的差距,有很多种函数来衡量,我们这里选用最简单的均方误差,调用函数为nn.MSELoss
output = net(input) #为列向量
target = torch.randn(10) #随机初始化10个值,为行向量
#view函数不改变tensor的值,只是对其长宽进行重构
#第一个-1表示不确定有几行,而第二个1表示1列。这样就把行向量转变为列向量了。
target = target.view(-1,1)
criterion = nn.MSELoss()
loss = criterion(output,target)
有了具体的输出和Loss function后,我们来计算LOSS关于各参数的梯度。进行反向传播,使用.backward()函数即可完成。此前要先把所有参数的梯度清零,然后查看conv1中 relu(W*a+b)里参数 W 或 偏置b 的梯度变化.
net.zero_grad() # zeroes the gradient buffers of all parameters
print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)
#print(net.conv1.weight.grad)
loss.backward()
print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)
#print(net.conv1.weight.grad)
out
conv1.bias.grad before backward
tensor([0., 0., 0., 0., 0., 0.])
conv1.bias.grad after backward
tensor([ 0.0029, -0.0122, 0.0044, 0.0115, 0.0076, 0.0122])
(4)更新权重
使用梯度下降法更新权重,可以自己定义公式,或者使用optim库
①自定义公式法
公式为:weight = weight - learning_rate * gradient
learning_rate = 0.01
for f in net.parameters():
f.data.sub_(f.grad.data * learning_rate)
②通用optim库法
import torch.optim as optim
#creat optimizer
optimizer = optim.SGD(net.parameters(),lr = 0.01)
#in your training loop:
optimizer.zero_grad() # zero the gradient buffers
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step() # Does the update