[人工智能]深度学习之目标检测——RCNN

Selective Search

• 背景:事先不知道需要检测哪个类别,且候选目标存在层级关系与尺度关系

• 常规解决方法：穷举法·，在原始图片上进行不同尺度不同大小的滑窗，获取每个可能的位置

  • 弊端：计算量大，且尺度不能兼顾

• Selective Search:通过视觉特征减少分类可能性

  

  • 算法步骤

    1. 基于图的图像分割方法初始化区域（图像分割为很多很多小块）
    2. 循环
       1. 使用贪心策略计算相邻区域相似度，每次合并相似的两块
       2. 直到剩下一块
    3. 结束

  • 如何保证特征多样性

    1. 颜色空间变换，RGB,i,Lab,HSV,

    2. 距离计算方式

       1. 颜色距离

          

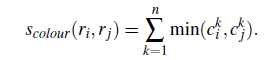
          1. 计算每个通道直方图
          2. 取每个对应bins的直方图最小值
          3. 直方图大小加权区域/总区域

       2. 纹理距离

          

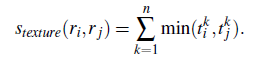
          1. 计算每个区域的快速sift特征(方向个数为8)
          2. 每个通道bins为2
          3. 其他用颜色距离

       3. 优先合并小区域

          1. 单纯通过颜色和纹理合并
             1. 合并区域会不断吞并，造成多尺度应用在局部问题上，无法全局多尺度
             2. 解决方法：给小区域更多权重

       4. .区域的合适度度距离

          1. 除了考虑每个区域特征的吻合程度，还要考虑区域吻合度(合并后的区域尽量规范，不能出现断崖式的区域)
          2. 直接需求就是区域的外接矩形的重合面积要大

          

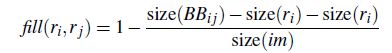
       5. 加权综合衡量距离

          1. 给予各种距离整合一些区域建议，加权综合考虑

             

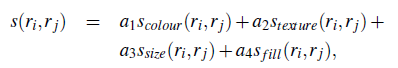
       6. 参数初始化多样性

          1. 通过多种参数初始化图像分割

       7. 区域打分

• 代码实现

# -*- coding: utf-8 -*-
from __future__ import division

import cv2 as cv
import skimage.io
import skimage.feature
import skimage.color
import skimage.transform
import skimage.util
import skimage.segmentation
import numpy


# "Selective Search for Object Recognition" by J.R.R. Uijlings et al.
#
#  - Modified version with LBP extractor for texture vectorization


def _generate_segments(im_orig, scale, sigma, min_size):
    """
        segment smallest regions by the algorithm of Felzenswalb and
        Huttenlocher
    """

    # open the Image
    im_mask = skimage.segmentation.felzenszwalb(
        skimage.util.img_as_float(im_orig), scale=scale, sigma=sigma,
        min_size=min_size)

    # merge mask channel to the image as a 4th channel
    im_orig = numpy.append(
        im_orig, numpy.zeros(im_orig.shape[:2])[:, :, numpy.newaxis], axis=2)
    im_orig[:, :, 3] = im_mask

    return im_orig


def _sim_colour(r1, r2):
    """
        calculate the sum of histogram intersection of colour
    """
    return sum([min(a, b) for a, b in zip(r1["hist_c"], r2["hist_c"])])


def _sim_texture(r1, r2):
    """
        calculate the sum of histogram intersection of texture
    """
    return sum([min(a, b) for a, b in zip(r1["hist_t"], r2["hist_t"])])


def _sim_size(r1, r2, imsize):
    """
        calculate the size similarity over the image
    """
    return 1.0 - (r1["size"] + r2["size"]) / imsize


def _sim_fill(r1, r2, imsize):
    """
        calculate the fill similarity over the image
    """
    bbsize = (
        (max(r1["max_x"], r2["max_x"]) - min(r1["min_x"], r2["min_x"]))
        * (max(r1["max_y"], r2["max_y"]) - min(r1["min_y"], r2["min_y"]))
    )
    return 1.0 - (bbsize - r1["size"] - r2["size"]) / imsize


def _calc_sim(r1, r2, imsize):
    return (_sim_colour(r1, r2) + _sim_texture(r1, r2)
            + _sim_size(r1, r2, imsize) + _sim_fill(r1, r2, imsize))


def _calc_colour_hist(img):
    """
        calculate colour histogram for each region

        the size of output histogram will be BINS * COLOUR_CHANNELS(3)

        number of bins is 25 as same as [uijlings_ijcv2013_draft.pdf]

        extract HSV
    """

    BINS = 25
    hist = numpy.array([])

    for colour_channel in (0, 1, 2):

        # extracting one colour channel
        c = img[:, colour_channel]

        # calculate histogram for each colour and join to the result
        hist = numpy.concatenate(
            [hist] + [numpy.histogram(c, BINS, (0.0, 255.0))[0]])

    # L1 normalize
    hist = hist / len(img)

    return hist


def _calc_texture_gradient(img):
    """
        calculate texture gradient for entire image

        The original SelectiveSearch algorithm proposed Gaussian derivative
        for 8 orientations, but we use LBP instead.

        output will be [height(*)][width(*)]
    """
    ret = numpy.zeros((img.shape[0], img.shape[1], img.shape[2]))

    for colour_channel in (0, 1, 2):
        ret[:, :, colour_channel] = skimage.feature.local_binary_pattern(
            img[:, :, colour_channel], 8, 1.0)
    # LBP特征
    return ret


def _calc_texture_hist(img):
    """
        calculate texture histogram for each region

        calculate the histogram of gradient for each colours
        the size of output histogram will be
            BINS * ORIENTATIONS * COLOUR_CHANNELS(3)
    """
    BINS = 10

    hist = numpy.array([])

    for colour_channel in (0, 1, 2):

        # mask by the colour channel
        fd = img[:, colour_channel]

        # calculate histogram for each orientation and concatenate them all
        # and join to the result
        hist = numpy.concatenate(
            [hist] + [numpy.histogram(fd, BINS, (0.0, 1.0))[0]])

    # L1 Normalize
    hist = hist / len(img)

    return hist


def _extract_regions(img):

    R = {}

    # get hsv image
    hsv = skimage.color.rgb2hsv(img[:, :, :3])

    # pass 1: count pixel positions
    for y, i in enumerate(img):

        for x, (r, g, b, l) in enumerate(i):

            # initialize a new region
            if l not in R:
                R[l] = {
                    "min_x": 0xffff, "min_y": 0xffff,
                    "max_x": 0, "max_y": 0, "labels": [l]}

            # bounding box
            if R[l]["min_x"] > x:
                R[l]["min_x"] = x
            if R[l]["min_y"] > y:
                R[l]["min_y"] = y
            if R[l]["max_x"] < x:
                R[l]["max_x"] = x
            if R[l]["max_y"] < y:
                R[l]["max_y"] = y

    # pass 2: calculate texture gradient
    tex_grad = _calc_texture_gradient(img)

    # pass 3: calculate colour histogram of each region
    for k, v in list(R.items()):

        # colour histogram
        masked_pixels = hsv[:, :, :][img[:, :, 3] == k]
        R[k]["size"] = len(masked_pixels / 4)
        R[k]["hist_c"] = _calc_colour_hist(masked_pixels)

        # texture histogram
        R[k]["hist_t"] = _calc_texture_hist(tex_grad[:, :][img[:, :, 3] == k])

    return R


def _extract_neighbours(regions):

    def intersect(a, b):
        if (a["min_x"] < b["min_x"] < a["max_x"]
                and a["min_y"] < b["min_y"] < a["max_y"]) or (
            a["min_x"] < b["max_x"] < a["max_x"]
                and a["min_y"] < b["max_y"] < a["max_y"]) or (
            a["min_x"] < b["min_x"] < a["max_x"]
                and a["min_y"] < b["max_y"] < a["max_y"]) or (
            a["min_x"] < b["max_x"] < a["max_x"]
                and a["min_y"] < b["min_y"] < a["max_y"]):
            return True
        return False

    R = list(regions.items())
    neighbours = []
    for cur, a in enumerate(R[:-1]):
        for b in R[cur + 1:]:
            if intersect(a[1], b[1]):
                neighbours.append((a, b))

    return neighbours


def _merge_regions(r1, r2):
    new_size = r1["size"] + r2["size"]
    rt = {
        "min_x": min(r1["min_x"], r2["min_x"]),
        "min_y": min(r1["min_y"], r2["min_y"]),
        "max_x": max(r1["max_x"], r2["max_x"]),
        "max_y": max(r1["max_y"], r2["max_y"]),
        "size": new_size,
        "hist_c": (
            r1["hist_c"] * r1["size"] + r2["hist_c"] * r2["size"]) / new_size,
        "hist_t": (
            r1["hist_t"] * r1["size"] + r2["hist_t"] * r2["size"]) / new_size,
        "labels": r1["labels"] + r2["labels"]
    }
    return rt


def selective_search(im_orig, scale=1.0, sigma=0.8, min_size=50):
    '''Selective Search

    Parameters
    ----------
        im_orig : ndarray
            Input image
        scale : int
            Free parameter. Higher means larger clusters in felzenszwalb segmentation.
        sigma : float
            Width of Gaussian kernel for felzenszwalb segmentation.
        min_size : int
            Minimum component size for felzenszwalb segmentation.
    Returns
    -------
        img : ndarray
            image with region label
            region label is stored in the 4th value of each pixel [r,g,b,(region)]
        regions : array of dict
            [
                {
                    'rect': (left, top, width, height),
                    'labels': [...],
                    'size': component_size
                },
                ...
            ]
    '''
    # 期待输入3通道图片
    assert im_orig.shape[2] == 3, "3ch image is expected"

    # load image and get smallest regions
    # region label is stored in the 4th value of each pixel [r,g,b,(region)]
    # 基于图方法生成图的最小区域，
    img = _generate_segments(im_orig, scale, sigma, min_size)
    # (512, 512, 4)
    # print(img.shape)
    # cv2.imshow("res1", im_orig)
    # print(type(img))
    # # img = cv2.cvtColor(img,cv2.COLOR_RGB2BGR)
    # cv2.imshow("res",img)
    # cv2.waitKey(0)
    # # print(img)
    # exit()

    if img is None:
        return None, {}

    imsize = img.shape[0] * img.shape[1]
    # 拓展区域
    R = _extract_regions(img)

    # extract neighbouring information
    neighbours = _extract_neighbours(R)

    # calculate initial similarities
    S = {}
    for (ai, ar), (bi, br) in neighbours:
        S[(ai, bi)] = _calc_sim(ar, br, imsize)

    # hierarchal search
    while S != {}:

        # get highest similarity
        i, j = sorted(S.items(), key=lambda i: i[1])[-1][0]

        # merge corresponding regions
        t = max(R.keys()) + 1.0
        R[t] = _merge_regions(R[i], R[j])

        # mark similarities for regions to be removed
        key_to_delete = []
        for k, v in list(S.items()):
            if (i in k) or (j in k):
                key_to_delete.append(k)

        # remove old similarities of related regions
        for k in key_to_delete:
            del S[k]

        # calculate similarity set with the new region
        for k in [a for a in key_to_delete if a != (i, j)]:
            n = k[1] if k[0] in (i, j) else k[0]
            S[(t, n)] = _calc_sim(R[t], R[n], imsize)

    regions = []
    for k, r in list(R.items()):
        regions.append({
            'rect': (
                r['min_x'], r['min_y'],
                r['max_x'] - r['min_x'], r['max_y'] - r['min_y']),
            'size': r['size'],
            'labels': r['labels']
        })

    return img, regions

• 测试

# -*- coding: utf-8 -*-
from __future__ import (
    division,
    print_function,
)
import cv2 as cv

import skimage.data
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import selectivesearch


def main():

    # loading astronaut image
    img = skimage.data.astronaut()
    # print(type(img))
    # img = cv.cvtColor(img,cv.COLOR_RGB2BGR)
    # cv.imshow("res",img)
    # cv.waitKey(0)
    # # print(img)
    # exit()
    # perform selective search
    img_lbl, regions = selectivesearch.selective_search(
        img, scale=500, sigma=0.9, min_size=10)

    candidates = set()
    for r in regions:
        # excluding same rectangle (with different segments)
        if r['rect'] in candidates:
            continue
        # excluding regions smaller than 2000 pixels
        if r['size'] < 2000:
            continue
        # distorted rects
        x, y, w, h = r['rect']
        if w / h > 1.2 or h / w > 1.2:
            continue
        candidates.add(r['rect'])

    # draw rectangles on the original image
    fig, ax = plt.subplots(ncols=1, nrows=1, figsize=(6, 6))
    ax.imshow(img)
    for x, y, w, h in candidates:
        print(x, y, w, h)
        rect = mpatches.Rectangle(
            (x, y), w, h, fill=False, edgecolor='red', linewidth=1)
        ax.add_patch(rect)

    plt.show()

if __name__ == "__main__":
    main()

• 测试结果

  

RCNN

算法步骤

1. 产生目标区域候选

2. CNN目标特征提取

   1. 使用的AlexNet
   2. imageNet预训练迁移学习，只训练全连接层
   3. 采用的全连接层输出(导致输入大小必须固定)

3. 目标种类分类器

4. SVM困难样本挖掘方法，正样本—>正样本 ，iou>0.3 == 负样本

5. 贪婪非极大值抑制 NMS

   1. 根据分类器的类别分类概率做排序，假设从小到大属于正样本的概率 分别为A、B、C、D、E、F。

   2. 从最大概率矩形框F开始，分别判断A~E与F的重叠度IOU是否大于某个设定的阈值

   3. 假设B、D与F的重叠度超过阈值，那么就扔掉B、D；并标记第一个矩形框F，是我们保留下来的。

   4. 从剩下的矩形框A、C、E中，选择概率最大的E，然后判断E与A、C的重叠度，重叠度大于一定的阈值，那么就扔掉；并标记E是我们保留下来的第二个矩形框。

      就这样一直重复，找到所有被保留下来的矩形框。

6. BoundingBox回归

   1. 微调回归框

   2. 一个区域位置

      1. 

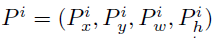
      2. 位置映射真实位置

         

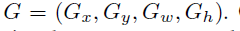
      3. 转换偏移量参数

         

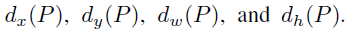
      4. 映射关系式

         

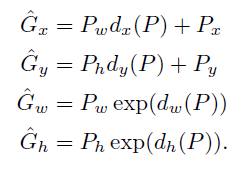
      5. 选用pool5层

         

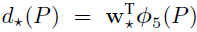
      6. 最小化w

         ?

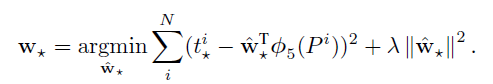
• 不使用全连接的输出作为非极大抑制的输入，而是训练很多的SVM。

• 因为CNN需要大量的样本，当正样本设置为真实BoundingBox时效果很差，而IOU>0.5相当于30倍的扩充了样本数量。而我们近将CNN结果作为一个初选，然后用困难负样本挖掘的SVM作为第二次筛选就好多了

• 缺点:时间代价太高了