[人工智能]机器学习入门

特征降维

降维的两种方式

特征选择

1 定义
数据中包含冗余或无关变量（或称特征、属性、指标等），旨在从原有特征中找出主要特征。
2 方法
Filter(过滤式)：主要探究特征本身特点、特征与特征和目标值之间关联
???? ① 方差选择法：低方差特征过滤
?? ? ②相关系数
Embedded (嵌入式)：算法自动选择特征（特征与目标值之间的关联）
????? ①决策树:信息熵、信息增益
? ? ? ②正则化：L1、L2
? ? ? ③?深度学习：卷积等
???2.1过滤式
??????2.1.1 低方差特征过滤
???????????????删除低方差的一些特征，前面讲过方差的意义。再结合方差的大小来考虑这个方式的角度。
???????? ? ? ?特征方差小：某个特征大多样本的值比较相近
?????? ? ? ? ?特征方差大：某个特征很多样本的值都有差别
????2.1.1.1API

sklearn.feature_selection.VarianceThreshold(threshold = 0.0)
删除所有低方差特征
Variance.fit_transform(X)
X:numpy array格式的数据[n_samples,n_features]
返回值：训练集差异低于threshold的特征将被删除。默认值是保留所有非零方差特征，即删除所有样本中具有相同值的特征。

例子：

from sklearn.feature_selection import VarianceThreshold
import pandas as pd
# 数据中包含冗余或无关变量（或称特征、属性、指标等），
# 旨在从原有特征中找出主要特征。

# sklearn.feature_selection.VarianceThreshold(threshold = 0.0)
# 删除所有低方差特征
# Variance.fit_transform(X)
# X:numpy array格式的数据[n_samples,n_features]
# 返回值：训练集差异低于threshold的特征将被删除。默认
# 值是保留所有非零方差特征，即删除所有样本中具有相同值
# 的特征。

#过滤低特征方差

#1获取数据
data=pd.read_csv("factor_returns.csv")
data=data.iloc[:,1:-2]
# print(data.info())

#2实例化一个转换器类
transfer=VarianceThreshold(threshold=3)

#3调用
data_new=transfer.fit_transform(data)

#4展示,二维数据.shape 看形状
print("data_new:\n",data_new,data_new.shape)
# (2318, 8) 2318行8列

2.1.2相关系数
皮尔逊相关系数(Pearson Correlation Coefficient)
反映变量之间相关关系密切程度的统计指标

from scipy.stats import pearsonr
import pandas as pd
# 相关系数的值介于–1与+1之间，即–1≤ r ≤+1。其性质如下：
# 当r>0时，表示两变量正相关，r<0时，两变量为负相关
# 当|r|=1时，表示两变量为完全相关，当r=0时，表示两变
# 量间无相关关系
# 当0<|r|<1时，表示两变量存在一定程度的相关。且|r|越
# 接近1，两变量间线性关系越
# 密切；|r|越接近于0，表示两变量的线性相关越弱
# 一般可按三级划分：|r|<0.4为低度相关；0.4≤|r|<0.7为
# 显著性相关；0.7≤|r|<1为高度线性相关


# from scipy.stats import pearsonr
# x : (N,) array_like
# y : (N,) array_like Returns: (Pearson’s correlation coefficient, p-value)

#计算某两个变量之间的相关系数
data=pd.read_csv("factor_returns.csv")
data=data.iloc[:,1:-2]
r=pearsonr(data["pe_ratio"],data["pb_ratio"])
print("相关系数:\n",r)
r2=pearsonr(data["revenue"],data["total_expense"])
print("revenue和total_expense的相关性",r2)

# scipy.stats.pearsonr(x, y)
# x和y为相同长度的两组数据
# 返回值 r, p-value
# r是相关系数，取值-1~1. 表示线性相关程度
# p-value越小，表示相关程度越显著。按照文档的说法
# “The p-values are not entirely reliable but
# are probably reasonable for datasets larger
#     than 500 or so.”，
# p-value在500个样本值以上有较高的可靠性

主成分分析（可以理解一种特征提取的方式）

什么是主成分分析(PCA)？

定义：高维数据转化为低维数据的过程，在此过程中可能会舍弃原有数据、创造新的变量

作用：是数据维数压缩，尽可能降低原数据的维数（复杂度），损失少量信息。

应用：回归分析或者聚类分析当中

from sklearn.decomposition import PCA
# sklearn.decomposition.PCA(n_components=None)
# 将数据分解为较低维数空间
# n_components:
# 小数：表示保留百分之多少的信息
# 整数：减少到多少特征
# PCA.fit_transform(X) X:numpy array格式的数据[n_samples,n_features]
# 返回值：转换后指定维度的array

#PCA降维
#1.获取数据
data=[[2,8,4,5],
[6,3,0,8],
[5,4,9,1]]
#2.实例化一个转换器类
transfer=PCA(n_components=2)
#3.调用
data_new=transfer.fit_transform(data)
#4.展示
print("data_new:\n",data_new)

import pandas as pd
from sklearn.decomposition import PCA
import numpy as np
# order_products__prior.csv：订单与商品信息
# 字段：order_id, product_id, add_to_cart_order, reordered
# products.csv：商品信息
# 字段：product_id, product_name, aisle_id, department_id
# orders.csv：用户的订单信息
# 字段：order_id,user_id,eval_set,order_number,….
# aisles.csv：商品所属具体物品类别
# 字段： aisle_id, aisle

#1.获取数据
order_products=pd.read_csv("./order_products__prior.csv")
products=pd.read_csv("./products.csv")
orders=pd.read_csv("./orders.csv")
aisles=pd.read_csv("./aisles.csv")

#2.合并表
tabel1=pd.merge(aisles,products,on="aisle_id")
tabel2=pd.merge(tabel1,order_products,on="product_id")
tabel3=pd.merge(tabel2,orders,on="order_id")
# print(tabel3.info())

#将user_id和aisle_id利用交叉表放在一起
tabel=pd.crosstab(tabel3["user_id"],tabel3["aisle_id"],margins=False)
print(tabel)

#PCA降维
transfer=PCA(n_components=0.95)
data_new=transfer.fit_transform(tabel)
print(data_new.shape)

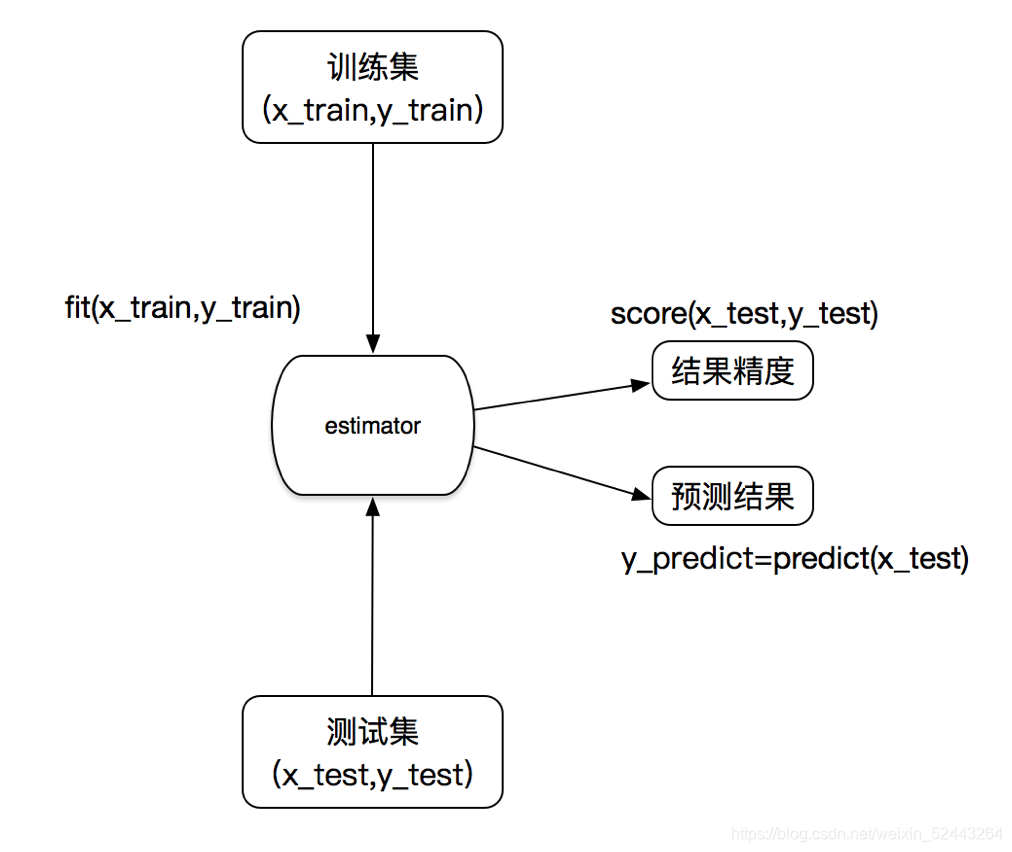
转换器和预估器

一、转换器
我们把特征工程的接口称之为转换器，其中转换器调用有这么几种形式

fit_transform
fit
transform

# 转换器 - 特征工程的父类
# 1.实例化(实例化的是一个转换器类)
# 2.调用fit_transform(对于文档建立分类词频矩阵，不能
# 同时调用)
# 标准化：
#     (x-mean) / std
#     fit_transform()
#         fit() 计算每一列的平均值、标准差
#         transform() (x-mean) / std进行最终的转换

估计器(sklearn机器学习算法的实现)
在sklearn中，估计器(estimator)是一个重要的角色，是一类实现了算法的API

1、用于分类的估计器：
sklearn.neighbors k-近邻算法
sklearn.naive_bayes 贝叶斯
sklearn.linear_model.LogisticRegression 逻辑回归
sklearn.tree 决策树与随机森林
2、用于回归的估计器：
sklearn.linear_model.LinearRegression 线性回归
sklearn.linear_model.Ridge 岭回归
3、用于无监督学习的估计器
sklearn.cluster.KMeans 聚类

K-近邻算法

1.1 定义
如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。

来源：KNN算法最早是由Cover和Hart提出的一种分类算法

1.2 距离公式
两个样本的距离可以通过如下公式计算，又叫欧式距离

K-近邻算法API

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm='auto')
n_neighbors：int,可选（默认= 5），k_neighbors查询默认使用的邻居数
algorithm：{‘auto’，‘ball_tree’，‘kd_tree’，‘brute’}，可选用于计算最近邻居的算法：‘ball_tree’将会使用 BallTree，‘kd_tree’将使用 KDTree。‘auto’将尝试根据传递给fit方法的值来决定最合适的算法。 (不同实现方式影响效率)

案例：预测签到位置

import pandas as pd
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV, train_test_split

# train.csv,test.csv
# row_id:登记事件的ID,无特别的含义，就是序号
# xy:坐标
# accuracy:定位准确性
# time:时间戳
# place_id:业务的ID，这是您预测的目标，签到点

#1.获取数据
from sklearn.preprocessing import StandardScaler

data=pd.read_csv("./train.csv")

#2.数据处理

#缩小数据范围 query("")
data=data.query("x<2.5 & x>2 & y<1.5 & y>1.0")

#处理时间戳，pd.to_datetime()转换为年月日时分秒  unit="s"用秒做单位
time_value=pd.to_datetime(data["time"],unit="s")
#DatetimeIndex()含有多个时间戳的数组
date=pd.DatetimeIndex(time_value)
print(date)
#添加列
data["day"]=date.day#日期
data["weekday"]=date.weekday#星期几
data["hour"]=date.hour#小时

#过滤签到次数少的地点
#根据"place_id"分组，把相同的place_id归到一类去，
# 然后计算有几次
place_count=data.groupby("place_id").count()["row_id"]#取"row_id"这一列
print(place_count)
place_count=place_count[place_count>3]#取placce_id大于三的place_id,即签到点大于三次的地方
#place_count 是Series类型的，它的index是"place_id"，所以isin后面接的是index
data_final=data[data["place_id"].isin(place_count.index)]
print(data_final)

#筛选特征值和目标值
x=data_final[["x","y","accuracy","day","weekday","hour"]]
y=data_final["place_id"]

#数据集划分
x_train,x_test,y_train,y_test=train_test_split(x,y)
#标准化
transfer=StandardScaler()
x_train=transfer.fit_transform(x_train)
x_test=transfer.transform(x_test)
#KNN估计器
estimator=KNeighborsClassifier()
param_dict={"n_neighbors":[1,3,5,7,9,11]}
estimator=GridSearchCV(estimator,param_grid=param_dict,cv=10)
estimator.fit(x_train,y_train)

#模型评估
#方法1：直接比对真实值和预测值
y_predict=estimator.predict(x_test)
print("y_predict\n",y_predict)
print("直接比对真实值和预测值:\n",y_test==y_predict)

#方法二
score=estimator.score(x_test,y_test)
print("准确率为:\n",score)







"""
DataFrame.isin(self, values)               

DataFrame中的每个元素是否包含在值中。

参数：values：iterable, Series, DataFrame或dict

如果所有标签都匹配，则结果仅在某个位置为true。

如果values是Series，那就是索引。

如果 values是一个dict，则键必须是必须匹配的列名。

如果值是DataFrame，则索引标签和列标签都必须匹配。

返回值：DataFrame
"""

#print(place_count[place_count>3].values)
# print(date.index)

模型选择与调优

API

sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)
对估计器的指定参数值进行详尽搜索
estimator：估计器对象
param_grid：估计器参数(dict){“n_neighbors”:[1,3,5]}
cv：指定几折交叉验证
fit：输入训练数据
score：准确率
结果分析：
bestscore:在交叉验证中验证的最好结果_
bestestimator：最好的参数模型
cvresults:每次交叉验证后的验证集准确率结果和训练集准确率结果

案例：鸢尾花模型调优

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV


# iris里有两个属性iris.data，iris.target。
# data是一个矩阵，每一列代表了萼片或花瓣的长宽，
# 一共4列，每一列代表某个被测量的鸢尾植物，一共
# 采样了150条记录。

# target是一个数组，存储了data中每条记录属于哪一类鸢
# 尾植物，所以数组的长度是150，数组元素的值因为共有3
# 类鸢尾植物，所以不同值只有3个。种类为山鸢尾、杂色鸢
# 尾、维吉尼亚鸢尾。

#1.获取数据集
iris=load_iris()

#2.数据集的划分
x_train,x_test,y_train,y_test=train_test_split(iris.data,iris.target,random_state=66)

#3.特征工程：标准化
transfer=StandardScaler()
x_train=transfer.fit_transform(x_train)
x_test=transfer.transform(x_test)#用x_train一样的平均值和方差进行转换

#4.KNN算法预估器
estimator=KNeighborsClassifier()

#加入网格搜索和交叉验证
#参数准备
param_dict={"n_neighbors":[1,3,5,7,9,11]}
estimator=GridSearchCV(estimator,param_grid=param_dict,cv=10)
estimator.fit(x_train,y_train)


#5.模型评估
#方法1：直接比对真实值和预测值
y_predict=estimator.predict(x_test)
print("y_predict\n",y_predict)
print("直接比对真实值和预测值:\n",y_test==y_predict)

#方法二
score=estimator.score(x_test,y_test)
print("准确率为:\n",score)

#最佳参数:best_params_
print("最佳参数\n" , estimator.best_params_)
#最佳结果:best_score_
print("最佳结果:\n",estimator.best_score_)
#最佳估计器
print("最佳估计器:\n",estimator.best_estimator_)
#交叉验证结果:cv_results_
print("交叉验证结果:\n", estimator.cv_results_)




# print(x_train.shape)
# print(x_test.shape)
# print(y_train.shape)
# print(y_test.shape)
# print(iris)

朴素贝叶斯算法

API

sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
朴素贝叶斯分类
alpha：拉普拉斯平滑系数

from sklearn.datasets import fetch_20newsgroups

# 联合概率：包含多个条件，且所有条件同时成立的概率
# 记作：P(A,B)
# 特性：P(A, B) = P(A)P(B)
# 条件概率：就是事件A在另外一个事件B已经发生条件下的
# 发生概率
# 记作：P(A|B)
# 特性：P(A1,A2|B) = P(A1|B)P(A2|B)
# 注意：此条件概率的成立，是由于A1,A2相互独立的结果
#  (记忆)
#相互独立：如果P(A,B)=P(A)P(B)，则称事件A和事件B
# 相互独立，这是相互独立的充要条件

#朴素：就是假设特征与特征之间相互独立
# 朴素贝叶斯算法：
#             朴素 + 贝叶斯
# 应用场景：
#             文本分类
#             单词作为特征
#         拉普拉斯平滑系数
# sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
# 朴素贝叶斯分类
# alpha：拉普拉斯平滑系数
#获取数据
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB

news=fetch_20newsgroups(subset="all")

#划分数据集
x_train,x_test,y_train,y_test=train_test_split(news.data,news.target)

#特征工程
transfer=TfidfVectorizer()
x_train=transfer.fit_transform(x_train)
x_test=transfer.transform(x_test)

#朴素贝叶斯算法预估器的流程
estimator=MultinomialNB(alpha = 1.0)
estimator.fit(x_train,y_train)#添加训练数据

#模型评估
#方法1：直接比对真实值和预测值
y_predict=estimator.predict(x_test)
print("y_predict\n",y_predict)
print("直接比对真实值和预测值:\n",y_test==y_predict)
#方法二
score=estimator.score(x_test,y_test)
print("准确率为:\n",score)




# 优点：
# 朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
# 对缺失数据不太敏感，算法也比较简单，常用于文本分类。
# 分类准确度高，速度快
# 缺点：
# 由于使用了样本属性独立性的假设，所以如果特征属性有关联时其效果不好


# data_home : str, default=None
#         Specify a download and cache folder for the datasets. If None,
#         all scikit-learn data is stored in '~/scikit_learn_data' subfolders.

#alpha的默认值是1
# sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
# 朴素贝叶斯分类
# alpha：拉普拉斯平滑系数

决策树算法

决策树API

class sklearn.tree.DecisionTreeClassifier(criterion=’gini’, max_depth=None,random_state=None)
决策树分类器
criterion:默认是’gini’系数，也可以选择信息增益的熵’entropy’
max_depth:树的深度大小
random_state:随机数种子
其中会有些超参数：max_depth:树的深度大小
其它超参数我们会结合随机森林讲解

用决策树对鸢尾花进行分类

from pandas.core.common import random_state
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.tree import DecisionTreeClassifier,export_graphviz
import graphviz

#因为是sklearn数据集，已经进行了很好的数据处理了，所以就不用人为的进行数据处理
#决策树算法不用计算距离，所以就不用对数据进行标准化


#1.获取数据集
iris=load_iris()

#2.划分数据集
x_train,x_test,y_train,y_test=train_test_split(iris.data,iris.target)

#3.决策树预估器 criterion:默认是’gini’系数，也可以选择信息增益的熵’entropy’
#max_depth:树的深度大小,这里因为书树的深度不会很深，所以没必要设置，默认就好
estimator=DecisionTreeClassifier(criterion="entropy")
estimator.fit(x_train,y_train)#填入数据，进行训练，得出模型

#4.决策树可视化 feature_names:特征名字，irir有这个属性
export_graphviz(estimator,out_file='iris_tree.dot',feature_names=iris.feature_names)
#读取决策树图片
with open("iris_tree.dot") as f:
    dot_graph=f.read()
graphviz.Source(dot_graph)

#5.模型评估
#方法1：直接比对真实值和预测值
y_predict=estimator.predict(x_test)
print("y_predict\n",y_predict)
print("直接比对真实值和预测值:\n",y_test==y_predict)

#方法二
score=estimator.score(x_test,y_test)
print("准确率为:\n",score)

案例：泰坦尼克号乘客生存预测

import pandas as pd
from sklearn.feature_extraction import DictVectorizer


#1.获取数据
from sklearn.tree import DecisionTreeClassifier, export_graphviz

train=pd.read_csv("train(1).csv")
test=pd.read_csv("test.csv")
y_test=pd.read_csv("gender_submission.csv")
y_test=list(y_test['Survived'])#测试集的目标值，要转换为列表
print(len(y_test))
#2.数据处理
#(1)处理缺失数据
#Age中的空值可用平均年龄来填充
train['Age'].fillna(train['Age'].mean(),inplace=True)
#Embarked中的空值可用登陆港口最多的填充
train["Embarked"].fillna("S",inplace=True)
#cabin中的数据缺失太严重，就不填充了
#Age中的空值可用平均年龄来填充
test['Age'].fillna(test['Age'].mean(),inplace=True)
#Embarked中的空值可用登陆港口最多的填充
test["Embarked"].fillna("S",inplace=True)

#3.特征选择，选择对分类结果有关键作用的特征
features=['Pclass','Sex','Age']
train_features=train[features]#训练集的特征值
train_target=train['Survived']#训练集的目标值
test_features=test[features]#测试集的特征值
#将特征值转换为字典
train_features=train_features.to_dict(orient ='records')
test_features=test_features.to_dict(orient ='records')
#字典特征抽取
# 实例化一个转换器类
transfer = DictVectorizer(sparse=False)
#调用
x_train=transfer.fit_transform(train_features)#字典特征抽取转换
x_test=transfer.transform(test_features)
#决策树
estimator=DecisionTreeClassifier(criterion="entropy")
estimator.fit(x_train,train_target)#填入数据，进行训练，得出模型
#5.模型评估
#方法1：直接比对真实值和预测值
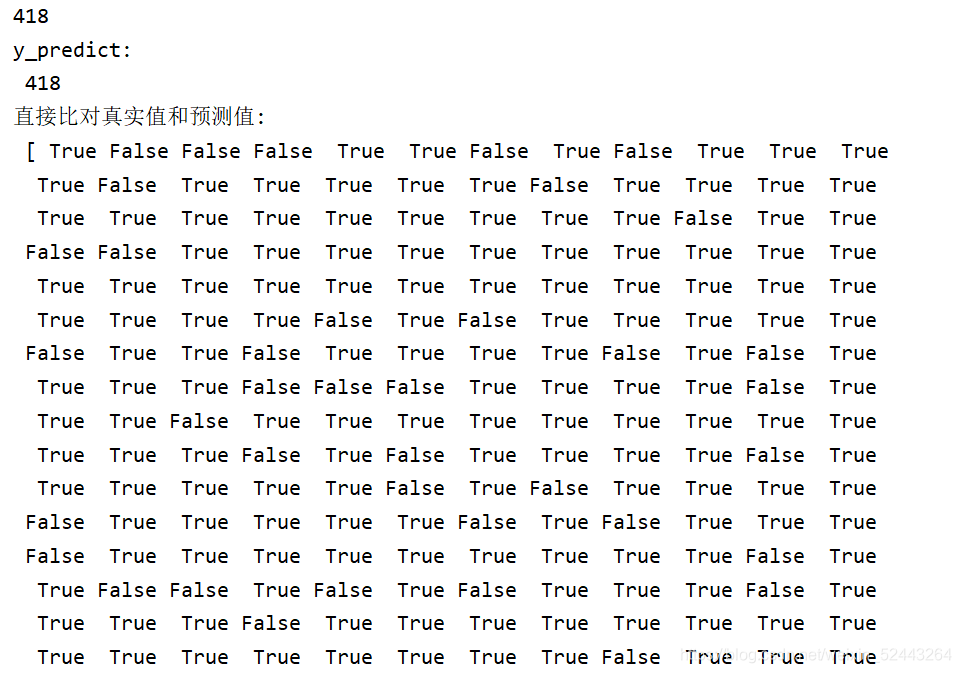
y_predict=estimator.predict(x_test)
print("y_predict:\n",len(y_predict))
print("直接比对真实值和预测值:\n",y_test==y_predict)

#4.决策树可视化 transfer.get_feature_names()获取特征名字
export_graphviz(estimator,out_file='titanic.dot',feature_names=transfer.get_feature_names())




#print(train.info())
# print(test.info())
#print(train['Embarked'].value_counts())
# S    644
# C    168
# Q     77
# Name: Embarked, dtype: int64




"""
pandas 的value_counts()函数可以对Series里面的
每个值进行计数并且排序。
value_counts(normalize=False, sort=True, ascending=False, bins=None, dropna=True)

参数:

1.normalize : boolean, default False　默认false，如为true，则以百分比的形式显示

2.sort : boolean, default True　默认为true,会对结果进行排序

3.ascending : boolean, default False　默认降序排序

4.bins : integer, 格式(bins=1),意义不是执行计算，而是把它们分成半开放的数据集合，只适用于数字数据

5.dropna : boolean, default True　默认删除na值
"""
"""
DataFrame.to_dict(*self*,orient='dict',into=)

都是转换为字典，但具体形式不同：
orient='dict',默认,字典套字典：{column:{index:value}}
orient ='list' ,字典里面为列表：{column：[values]}
orient ='series',字典里为series形式：{column: Series(values)}
orient ='split',字典里是数据对应列表：{'index':[index],'columns':[columns],'data': [values]}
orient ='records',转化后是 list形式：[{column: value},...,{column:value}]
orient ='index',字典里面同样有字典：{index:{column:value}}
"""

决策树总结
优点：
简单的理解和解释，树木可视化。
缺点：
决策树学习者可以创建不能很好地推广数据的过于复杂的树，这被称为过拟合。
改进：
减枝cart算法(决策树API当中已经实现，随机森林参数调优有相关介绍)
随机森林

集成学习方法之随机森林

什么是随机森林
在机器学习中，随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。
API

class sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None, min_samples_split=2)

随机森林分类器
n_estimators：integer，optional（default = 10）森林里的树木数量120,200,300,500,800,1200
criteria：string，可选（default =“gini”）分割特征的测量方法
max_depth：integer或None，可选（默认=无）树的最大深度 5,8,15,25,30
max_features="auto”,每个决策树的最大特征数量
If "auto", then max_features=sqrt(n_features).
If "sqrt", then max_features=sqrt(n_features) (same as "auto").
If "log2", then max_features=log2(n_features).
If None, then max_features=n_features.
bootstrap：boolean，optional（default = True）是否在构建树时使用放回抽样
min_samples_split:节点划分最少样本数
min_samples_leaf:叶子节点的最小样本数
超参数：n_estimator, max_depth, min_samples_split,min_samples_leaf

用随机森林对泰坦尼克号进行预测
1、 什么是集成学习方法
集成学习通过建立几个模型组合的来解决单一预测问题。
它的工作原理是生成多个分类器/模型，各自独立地学习
和作出预测。这些预测最后结合成组合预测，因此优于任
何一个单分类的做出预测。
2、 什么是随机森林
在机器学习中，随机森林是一个包含多个决策树的分类器，
#并且 其输出的类别是由个别树输出的类别的众数而定。

import pandas as pd
from sklearn.feature_extraction import DictVectorizer
from sklearn.ensemble import RandomForestClassifier

#1.获取数据
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeClassifier, export_graphviz


train=pd.read_csv("train(1).csv")
test=pd.read_csv("test.csv")
y_test=pd.read_csv("gender_submission.csv")
y_test=list(y_test['Survived'])#测试集的目标值，要转换为列表
print(len(y_test))
#2.数据处理
#(1)处理缺失数据
#Age中的空值可用平均年龄来填充
train['Age'].fillna(train['Age'].mean(),inplace=True)
#Embarked中的空值可用登陆港口最多的填充
train["Embarked"].fillna("S",inplace=True)
#cabin中的数据缺失太严重，就不填充了
#Age中的空值可用平均年龄来填充
test['Age'].fillna(test['Age'].mean(),inplace=True)
#Embarked中的空值可用登陆港口最多的填充
test["Embarked"].fillna("S",inplace=True)

#3.特征选择，选择对分类结果有关键作用的特征
features=['Pclass','Sex','Age']
train_features=train[features]#训练集的特征值
train_target=list(train['Survived'])#训练集的目标值
test_features=test[features]#测试集的特征值
#将特征值转换为字典
train_features=train_features.to_dict(orient ='records')
test_features=test_features.to_dict(orient ='records')
#字典特征抽取
# 实例化一个转换器类
transfer = DictVectorizer(sparse=False)
#调用
x_train=transfer.fit_transform(train_features)#字典特征抽取转换
x_test=transfer.transform(test_features)

#随机森林
ran=RandomForestClassifier()


#加入网格搜索和交叉验证
#参数准备
param_dict={"n_estimators":[120,200,300,500,800,1200],"max_depth":[5,8,15,25,30]}
estimator=GridSearchCV(ran,param_grid=param_dict,cv=3)
estimator.fit(x_train,train_target)

#5.模型评估
#方法1：直接比对真实值和预测值
y_predict=estimator.predict(x_test)
print("y_predict:\n",len(y_predict))
print("直接比对真实值和预测值:\n",y_test==y_predict)

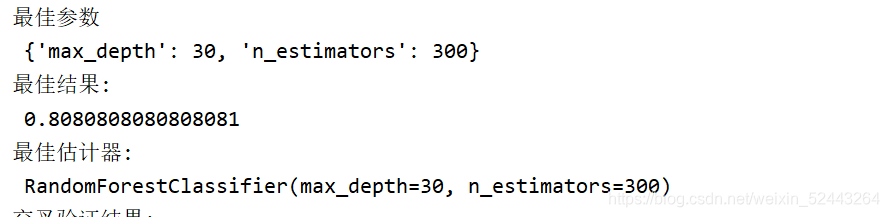
#最佳参数:best_params_
print("最佳参数\n" , estimator.best_params_)
#最佳结果:best_score_
print("最佳结果:\n",estimator.best_score_)
#最佳估计器
print("最佳估计器:\n",estimator.best_estimator_)
#交叉验证结果:cv_results_
print("交叉验证结果:\n", estimator.cv_results_)

线性回归

定义与公式
线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。

特点：只有一个自变量的情况称为单变量回归，大于一个自变量情况的叫做多元回归

线性回归API

sklearn.linear_model.LinearRegression(fit_intercept=True)
通过正规方程优化
fit_intercept：是否计算偏置
LinearRegression.coef_：回归系数
LinearRegression.intercept_：偏置
sklearn.linear_model.SGDRegressor(loss="squared_loss", fit_intercept=True, learning_rate ='invscaling', eta0=0.01)
SGDRegressor类实现了随机梯度下降学习，它支持不同的loss函数和正则化惩罚项来拟合线性回归模型。
loss:损失类型
loss=”squared_loss”: 普通最小二乘法
fit_intercept：是否计算偏置
learning_rate : string, optional
学习率填充
'constant': eta = eta0
'optimal': eta = 1.0 / (alpha * (t + t0)) [default]
'invscaling': eta = eta0 / pow(t, power_t)
power_t=0.25:存在父类当中
对于一个常数值的学习率来说，可以使用learning_rate=’constant’ ，并使用eta0来指定学习率。
SGDRegressor.coef_：回归系数
SGDRegressor.intercept_：偏置

线性回归之波士顿房价预测

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression,SGDRegressor
from sklearn.metrics import mean_squared_error
def liner1():

    #获取数据
    boston=load_boston()

    #划分数据集
    x_train,x_test,y_train,y_test=train_test_split(boston.data,boston.target)

    #标准化,因为有的数据过大的话就会导致权重计算的不准确
    transfer=StandardScaler()
    x_train=transfer.fit_transform(x_train)
    x_test=transfer.transform(x_test)

    #预估器
    estimator=LinearRegression()
    estimator.fit(x_train,y_train)

    #得出模型
    print("正规方程权重系数为:\n",estimator.coef_)
    print("正规方程偏置为:\n",estimator.intercept_)

    #模型评估
    y_predict=estimator.predict(x_test)
    print("预测房价:\n",y_predict)
    error=mean_squared_error(y_test,y_predict)
    print("正规方程-均方误差为:\n",error)
    return None

def liner2():
    #获取数据
    boston=load_boston()

    #划分数据集
    x_train,x_test,y_train,y_test=train_test_split(boston.data,boston.target)

    #标准化,因为有的数据过大的话就会导致权重计算的不准确
    transfer=StandardScaler()
    x_train=transfer.fit_transform(x_train)
    x_test=transfer.transform(x_test)

    #预估器
    estimator=SGDRegressor()
    estimator.fit(x_train,y_train)

    #得出模型
    print("梯度下降权重系数为:\n",estimator.coef_)
    print("梯度下降偏置为:\n",estimator.intercept_)

    #模型评估
    y_predict = estimator.predict(x_test)
    print("预测房价:\n", y_predict)
    #线性回归性能评估
    error = mean_squared_error(y_test, y_predict)
    print("梯度下降-均方误差为:\n", error)
if __name__=="__main__":

    liner1()
    liner2()

欠拟合与过拟合

定义
过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合， 但是在测试数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。(模型过于复杂)
欠拟合：一个假设在训练数据上不能获得更好的拟合，并且在测试数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。(模型过于简单)

原因以及解决办法
欠拟合原因以及解决办法
原因：学习到数据的特征过少
解决办法：增加数据的特征数量
过拟合原因以及解决办法
原因：原始特征过多，存在一些嘈杂特征， 模型过于复杂是因为模型尝试去兼顾各个测试数据点
解决办法：
正则化
在这里针对回归，我们选择了正则化。但是对于其他机器学习算法如分类算法来说也会出现这样的问题，除了一些算法本身作用之外（决策树、神经网络），我们更多的也是去自己做特征选择，包括之前说的删除、合并一些特征
正则化类别
L2正则化
作用：可以使得其中一些W的都很小，都接近于0，削弱某个特征的影响
优点：越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象
Ridge回归
L1正则化
作用：可以使得其中一些W的值直接为0，删除这个特征的影响
LASSO回归

岭回归

岭回归，其实也是一种线性回归。只不过在算法建立回归方程时候，加上正则化的限制，从而达到解决过拟合的效果
API

sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver="auto", normalize=False)
具有l2正则化的线性回归
alpha:正则化力度，也叫 λ
λ取值：0~1 1~10
solver:会根据数据自动选择优化方法
sag:如果数据集、特征都比较大，选择该随机梯度下降优化
normalize:数据是否进行标准化
normalize=False:可以在fit之前调用preprocessing.StandardScaler标准化数据
Ridge.coef_:回归权重
Ridge.intercept_:回归偏置

岭回归之波士顿房价预测

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression,Ridge
from sklearn.metrics import mean_squared_error

# 获取数据
boston = load_boston()

# 划分数据集
x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target)

# 标准化,因为有的数据过大的话就会导致权重计算的不准确
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 预估器
estimator = Ridge()
estimator.fit(x_train, y_train)

# 得出模型
print("岭回归权重系数为:\n", estimator.coef_)
print("岭回归偏置为:\n", estimator.intercept_)

# 模型评估
y_predict = estimator.predict(x_test)
print("预测房价:\n", y_predict)
error = mean_squared_error(y_test, y_predict)
print("岭回归-均方误差为:\n", error)

逻辑回归

# 逻辑回归（Logistic Regression）是机器学习中的一
# 种分类模型，逻辑回归是一种分类算法，虽然名字中带
# 有回归，但是它与回归之间有一定的联系。由于算法的
# 简单和高效，在实际中应用非常广泛
# 4.4 分类算法-逻辑回归与二分类
#     4.4.1 逻辑回归的应用场景
#         广告点击率 是否会被点击
#         是否为垃圾邮件
#         是否患病
#         是否为金融诈骗
#         是否为虚假账号
#         正例 / 反例(二分类)
#     4.4.2 逻辑回归的原理
#         线型回归的输出 就是 逻辑回归 的 输入
#         激活函数（把输入结果带入激活函数进行分类）
#             sigmoid函数 [0, 1](可以设定大于阈值就属于这个类别，小于阈值就不属于这个类别)
#             [0,1]可以看成是概率值，算出结果后对比属于哪个概率范围
#             1/(1 + e^(-x))(x部分就代入h(w))
#         假设函数/线性模型
#             1/(1 + e^(-(w1x1 + w2x2 + w3x3 + …… + wnxn + b)))
#            需要解决的是就是得到合理的权重和偏置
#         损失函数
#             (y_predict - y_true)平方和/总数
#             逻辑回归的真实值/预测值--> 是否属于某个类别
#             对数似然损失
#             log 2 x
#         优化损失
#             梯度下降

逻辑回归之癌症预测

import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
#1.获取数据
from sklearn.model_selection import train_test_split

column_name = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape',
                   'Marginal Adhesion', 'Single Epithelial Cell Size', 'Bare Nuclei', 'Bland Chromatin',
                   'Normal Nucleoli', 'Mitoses', 'Class']

#添加列元素，原数据集没有列名pd.read_csv(names=)
data=pd.read_csv("breast-cancer-wisconsin.csv",names=column_name)

#2.缺失值处理
#(1)把'?'替换为nan
data=data.replace(to_replace='?',value=np.nan)
#(2)dropna()删除用NaN标记的数据
data.dropna(inplace=True)

#3.划分数据集
#print(data.head())
#(1)筛选特征值和目标值
x=data.iloc[:,1:-1]#选第一列(取到)到最后一列(取不到)
y=data["Class"]#是否为癌症
# print(x)
x_train,x_test,y_train,y_test=train_test_split(x,y)

#4.标准化,因为逻辑回归模型还是有必要标准化的
transfer=StandardScaler()
x_train=transfer.fit_transform(x_train)#训练集
x_test=transfer.transform(x_test)#测试集

#5.逻辑回归的预估器流程
estimator=LogisticRegression()
estimator.fit(x_train,y_train)#输入训练集数据得出模型

#6.查看逻辑回归的模型参数
print("回归系数:\n",estimator.coef_)
print("偏置:\n",estimator.intercept_)

#7.模型评估
#方法1：直接比对真实值和预测值
y_predict=estimator.predict(x_test)
print("y_predict\n",y_predict)
print("直接比对真实值和预测值:\n",y_test==y_predict)

#方法二
score=estimator.score(x_test,y_test)
print("准确率为:\n",score)

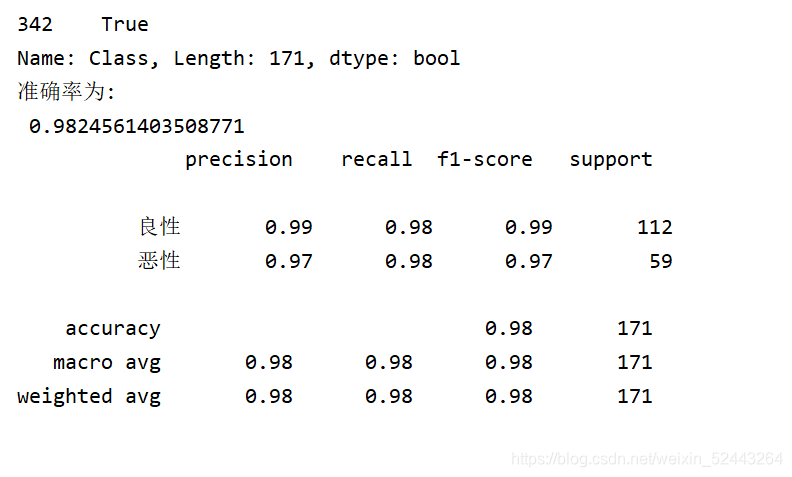
#查看精确率和召回率，2代表的类别是良性，4代表的类别是恶性
#y_test是真实值 y_predict是预估值 labels是每个类别用什么数字表示的
report=classification_report(y_test,y_predict,labels=[2,4],target_names=["良性","恶性"])
print(report)
#F1-score，反映了模型的稳健型
#support 样本数量

"""
data是DataFrame类型的数据，如果要替换里面的个别数据可以用
replace()函数
replace(self, to_replace=None, value=None, 
inplace=False, limit=None, regex=False, 
method='pad', axis=None)
data.isnull().any()查看每一列的是否含有缺失值

 3 F1-score 模型的稳健型
   总共有100个人，如果99个样本癌症，1个样本非癌症 - 样本不均衡(正例即得癌症的样本过多，但反例即没得癌症的样本数量过少)
   不管怎样我全都预测正例(默认癌症为正例) - 不负责任的模型            准确率：99%
    召回率：99/99 = 100%(真实为癌症的样本中预测结果为癌症比例)
    精确率：99%
    F1-score: 2*99%/ 199% = 99.497%
    
    
"""