[人工智能]PyTorch 简介

神经网络（Neural Network）

? 所有神经元间的连接都是不可更换的，不能凭空产生新连接。

比如：伸手吃糖动作。

? 准备非常多吃糖的学习数据，放入神经网络，糖的信号通过数据传递到手，对比手的动作是不是讨糖来修改神经元强度。（修改过程为误差反向传递 相当于将传过来的信号传回去），检查负责传递的神经元对于讨糖的动作有无贡献，让它反思修正。

? 也就是说人工神经网络通过正向和反向传播更新神经元形成更好的神经系统。 本质上, 是能让计算机处理和优化的数学模型

梯度下降（Gradient Descent）

? 神经网络原理：梯度下降机制

1. optimization(优化问题)

   牛顿法, 最小二乘法, 梯度下降法 等等

   梯度下降（Gradient Descent）是优化问题（optimization）分支的一种，梯度(gradient)=求导求微分

2. 误差方程 (Cost Function)：

   计算预测出来的和实际中的值有多大差别。在预测数值的问题中, 常用平方差 (Mean Squared Error) 来代替。

? 简化方程, W：神经网络中的参数, x, y ：数据, 因为 xy 都是实在的数据点, 在这个假设情况中, 是多少无所谓, 继续简化, (不正确, 只是为了看效果), 所以得到现在误差值曲线.

? 假设初始化的 W 在这个位置. 这的斜率是这条线, 也就是梯度下降中的梯度. 从图中可以看出, Cost 误差最小的时候正是这条 cost 曲线最低的地方, 不过在蓝点的 W不知道, 他目前知道的就是梯度线为自己在这个位置指出的一个下降方向, 就朝着这个蓝色梯度的方向下降一点点. 再做一条切线, 发现还能下降,就朝着梯度的方向继续下降, 这时, 再展示出现在的梯度, 因为梯度线已经躺平,已经指不出哪边是下降的方向了, 所以这时就找到了 W 参数的最理想值. 简而言之, 就是找到梯度线躺平的点. 可是神经网络的梯度下降可没这么简单.

3. 全局、最优局部

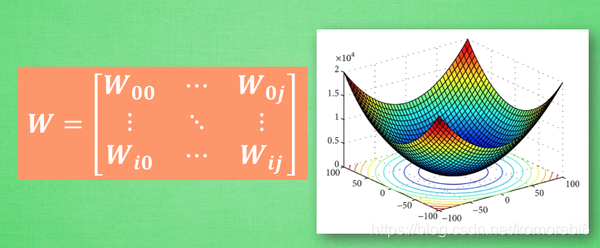
w不止一个，在通常神经网络中, 误差曲线可没这么优雅.

神经网络黑盒

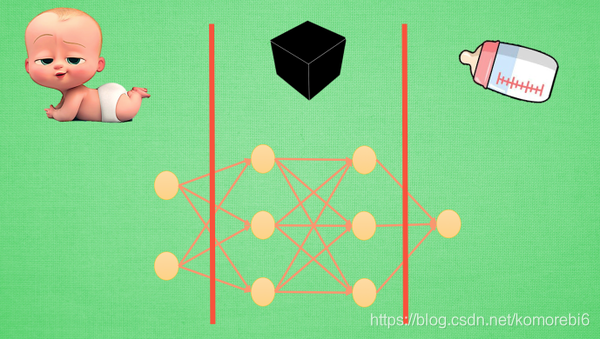
1. 神经网络分区

   输入端, 黑盒, 输出端.

   ? 输入端是一个宝宝（特征(features)）, 输出端是一个奶瓶. 对于神经网络, 传统的理解是, 中间的这两层神经层在对输入信息进行加工, 好让自己的输出信息和奶瓶吻合.

   ? 将左边的红线移动一下，现在的输入端增加了一层, 原本认定为黑盒的一部分被照亮,变成已知部分. 我们将最左边两层的神经层共同看成输入端.这时的输入端通过了一层神经网络加工, 变成了另外一种宝宝的形象,计算机能理解，

   将神经网络第一层加工后的宝宝叫做代表特征(feature representation).

   ? 如果再次移动红线, 黑盒就消失了, 这时原本在黑盒里的所有神经层都被照亮. 原本的代表特征再次被加工, 变成了另一种代表特征, 同样, 再次加工形成的代表特征通常只有计算机自己 能够理解

   ? 黑盒加工处理：将一种代表特征转换成另一种代表特征, 一次次特征之间的转换, 也就是一次次的更有深度的理解.

2. 迁移学习

   ? 对于一个有分类能力的神经网络, 有时候只需要这套神经网络的理解能力, 并拿这种能力去处理其他问题. 所以保留它的代表特征转换能力. 因为有了这种能力, 就能将复杂的图片像素信息转换成更少量, 但更精辟的信息。

   ? 比如将手写数字变成的3个点信息. 然后将这个神经网络的输出层给拆掉. 套上另外一个神经网络, 用这种移植的方式再进行训练, 让它处理不同的问题。

图源及笔记： https://mofanpy.com/