第一章 引言
因为第一章是引言部分,没有什么特别需要做笔记的,所以就没有单独开一章写,和第二章放在了一起。
引言部分翻译了花书各个章节之间的关系。
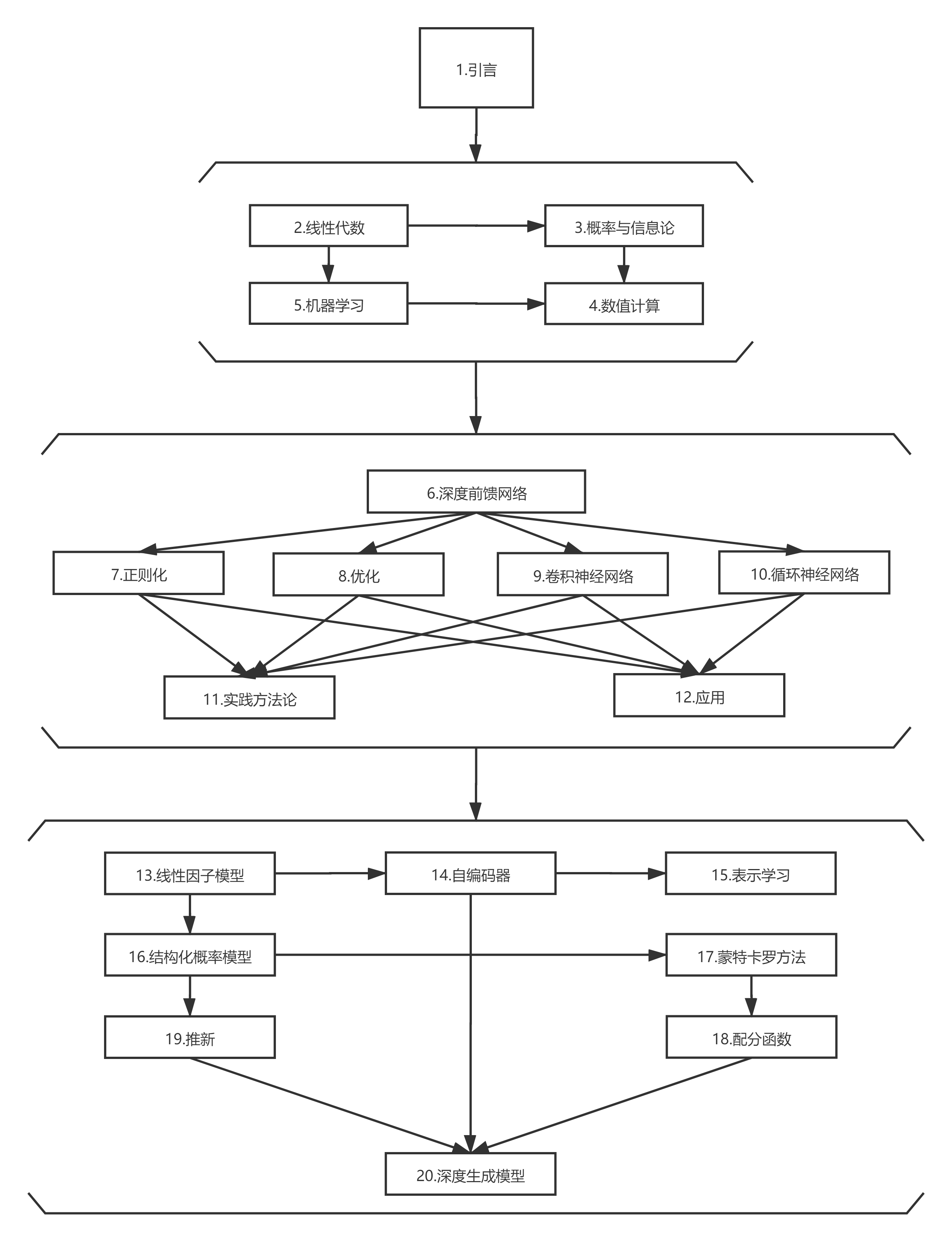
第二章 线性代数
一、思维导图

二、线性代数基本概念
1.线性代数基本概念
? 基本概念:
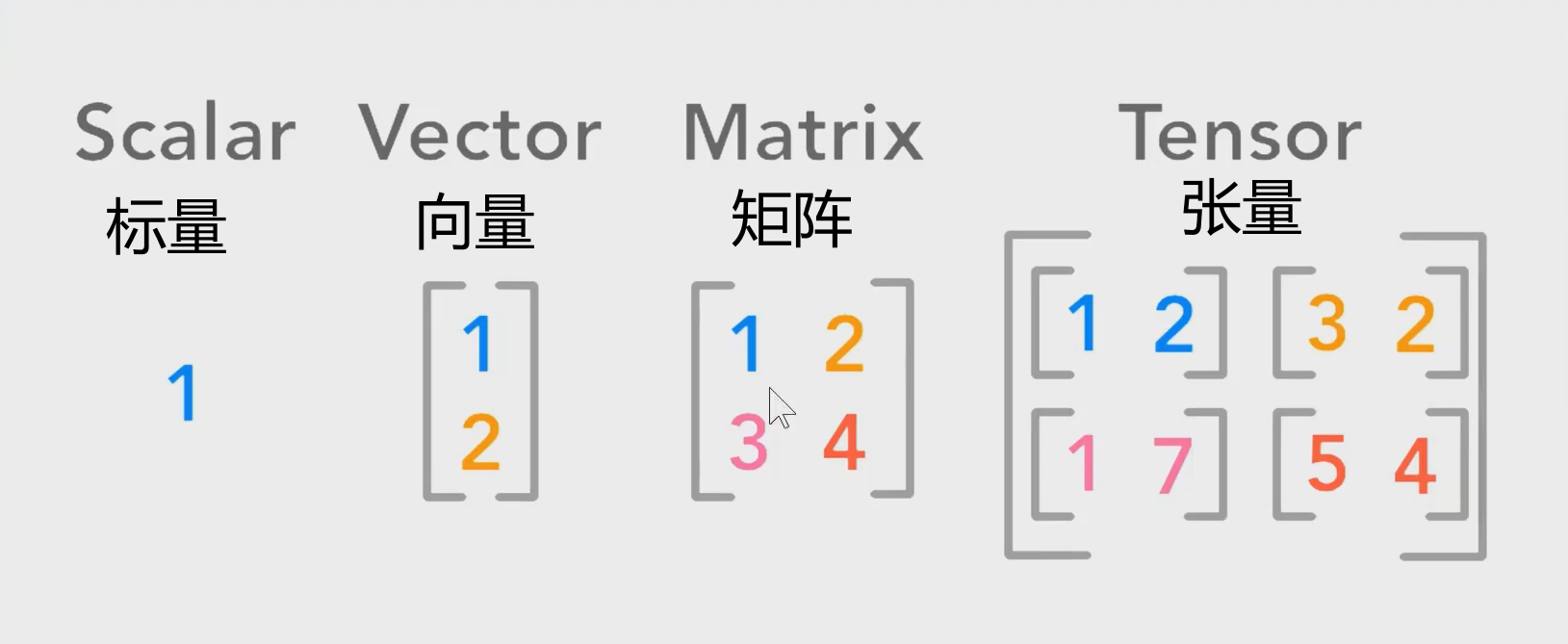
? 标量就是一个数,向量是一维的,矩阵是二维的,张量是三维或者更高维。
? 在Python中使用NumPy库进行矩阵的操作。
? 矩阵的转置:
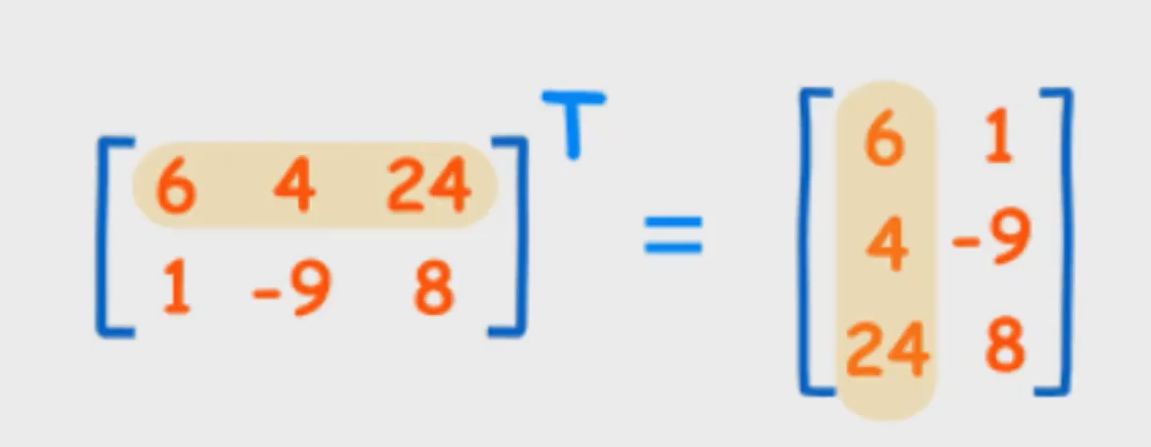
2.线性代数常用运算
-
矩阵乘法(点积):
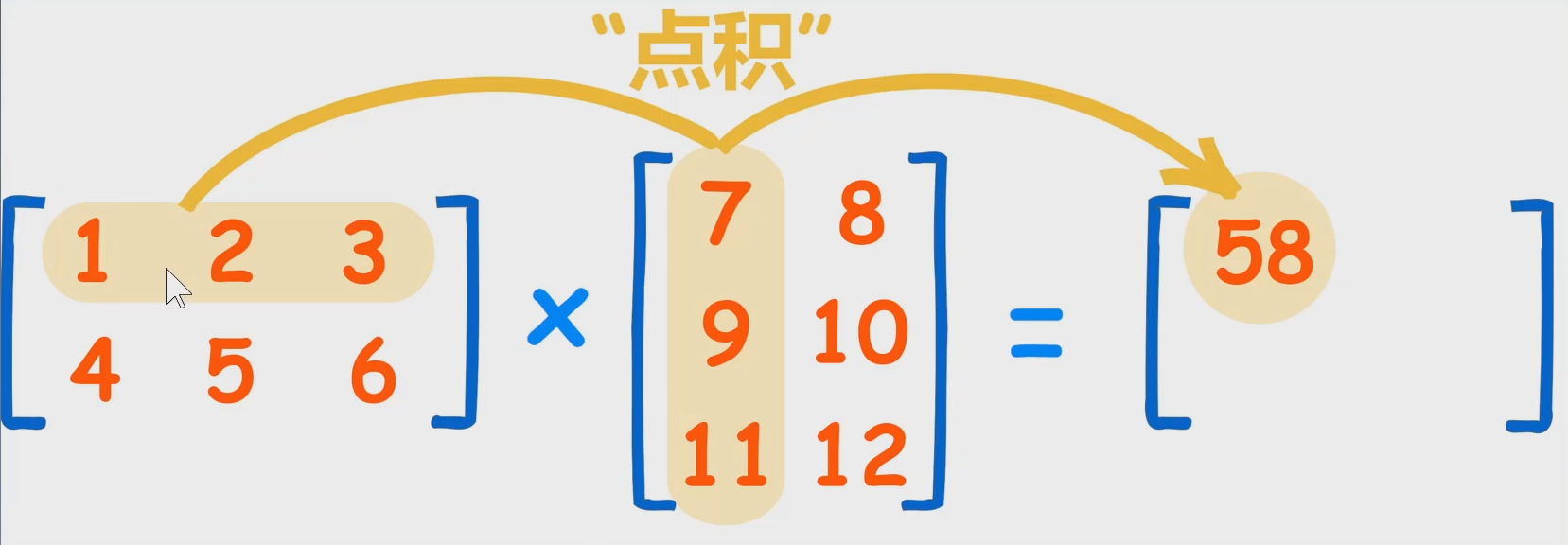
-
单位矩阵
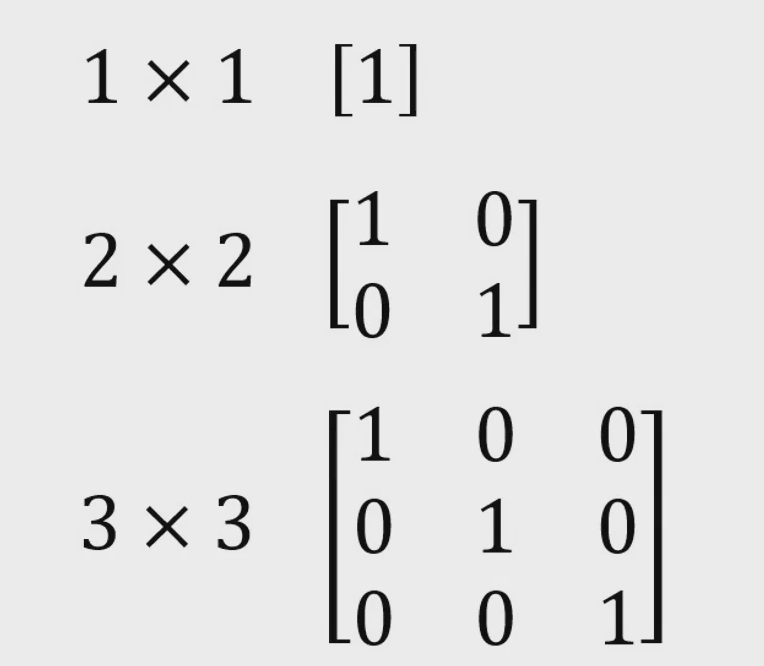
主对角线上的元素为1,其他元素为0。
-
范数:

当p取1时,为L1范数,又称曼哈顿距离、街区距离,本质上是绝对值的和。
当p取2时,为L2范数,本质是欧氏距离,多维空间中两点的距离便是平方和再开根号。
当p无穷大时,就是切比雪夫距离。
-
矩阵的奇异值分解:
矩阵的分解是指把一个矩阵分解成多个矩阵的乘积。
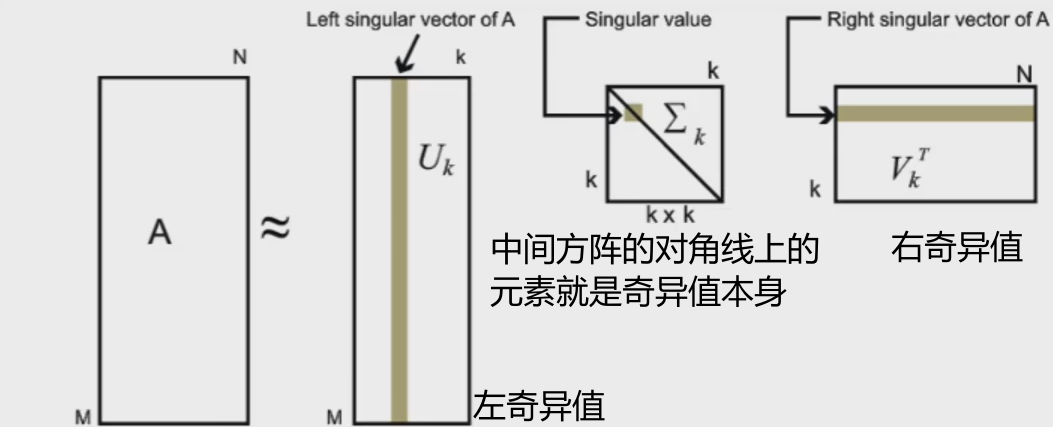
-
矩阵的迹运算:
矩阵的迹就是主对角线元素的求和。
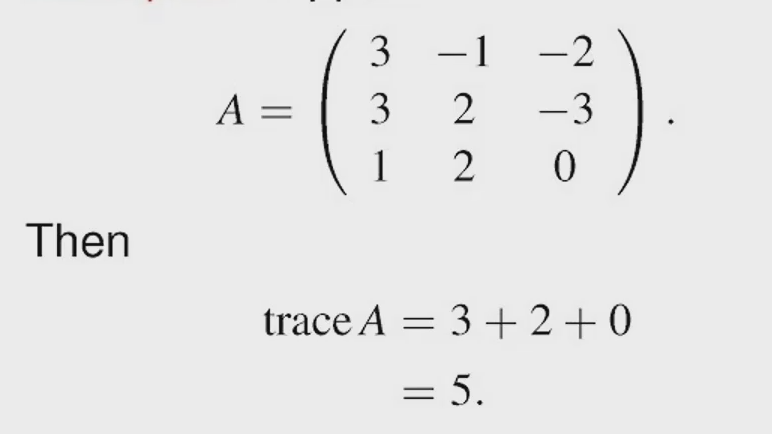
三、实例:主成分分析
? 主成分分析(PCA)是一种线性降维的算法,即把高维数据映射到低维。比如说一个二维空间xy平面直角坐标系,把这个二维空间的数据映射到这个直线上,直线是一个一维空间,就可以只看他们在一维上的分布了。
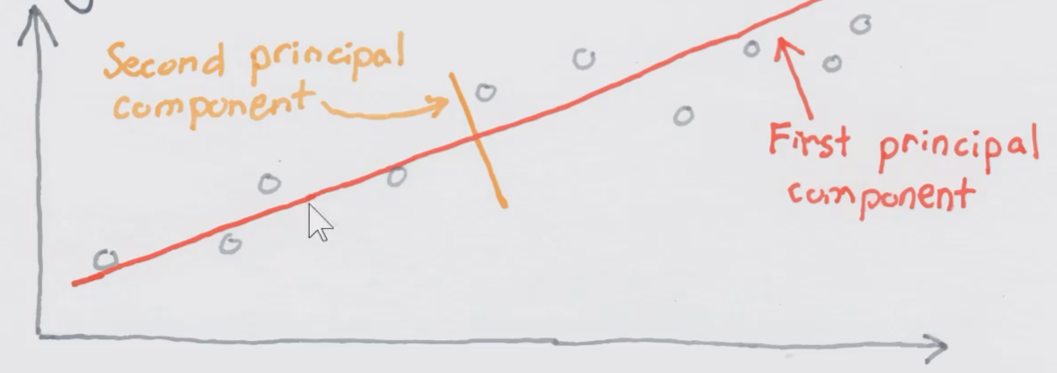
? 那如何降维能够尽可能大的保留在高维的信息呢?比如说对于一个人而言,如果把一个人从三维拍扁拍成二维纸片人,那从哪个方向拍是能保留最大的信息呢?是从左往右侧面的拍,从上往下,从头顶往下拍,还是从前往后把人的这个大字拍下来呢?那肯定是从前往后把这个大字拍下来,能够保留最多的信息。主成分分析其实就是想找到这个拍的这个方向,能够保留更可能大的保留高维空间的信息。
? 上图红线就是第一主成分,跟这条红线正交的方向,称之为第二组成分。把这个数据拍到这个红线上,就能够最大程度的保留在他在二维空间中的信息。
? 主成分分析关键的就是要找到第一主成分和第二主成分,第一主成分和第二主成分其实对应的就是协方差矩阵的特征值和特征向量。
四、规划学习路径
? 本科数学知识:微积分、线性代数、概率论、数值分析、工程数学
? 研究生数学知识:矩阵论、最优化理论
? 深度学习基础:神经网络的权重、反向传播
本科需要学习的只是基本在大一大二期间都学过了,只是我当时都没有认真听,此时我留下了悔恨的泪水,出来混迟早是要还的。up“同济子豪兄”推荐了山东大学的线性代数课,所以我打算先从线代开始补起,希望能尽快还清学习债务。
本笔记是根据B站up“深度之眼官方账号”的话术导读写的,仅用于自我总结学习。