绪论
卷积神经网络应用
1.分类
2.检索
3.检测
4.分割
传统神经网络VS卷积神经网络
深度学习步骤
1.搭建神经网络结构
2.找到一个合适的损失函数(交叉熵损失,均方误差,…)
3.找到一个合适的优化函数,更新参数(反向传播(BP),随机梯度下降(SGD)…)
损失函数
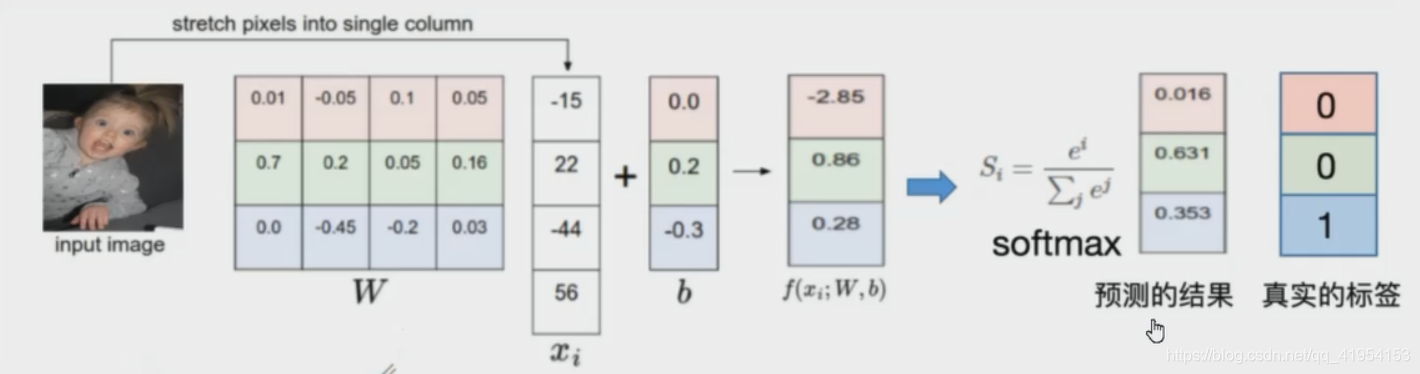
1.给定W,可以由像素映射到类目得分
2.损失函数是用来衡量吻合度的
3.可以调整参数/权重W,使得映射的结果和实际类别吻合
4.常用分类损失:
交
叉
熵
损
失
:
L
o
s
s
=
?
∑
i
y
i
l
n
y
i
p
h
i
n
g
e
l
o
s
s
:
L
(
y
,
f
(
x
)
)
=
m
a
x
(
0
,
1
?
y
f
(
x
)
)
.
.
.
交叉熵损失:Loss=-\sum_iy_ilny_i^p {\quad \quad} hinge loss:L(y,f(x))=max(0,1-yf(x)) \quad \quad ...
交叉熵损失:Loss=?i∑?yi?lnyip?hingeloss:L(y,f(x))=max(0,1?yf(x))...
5.常用回归损失:
均
方
误
差
:
M
S
E
=
∑
i
=
1
n
(
y
i
?
y
i
p
)
2
平
均
绝
对
值
误
差
(
L
1
损
失
)
:
M
A
E
=
∑
i
=
1
n
∣
y
i
?
y
i
p
∣
.
.
.
均方误差:MSE =\sum_{i=1}^n(y_i-y_i^p)^2 \quad \quad 平均绝对值误差(L1损失):MAE =\sum_{i=1}^n|y_i-y_i^p| \quad \quad ...
均方误差:MSE=i=1∑n?(yi??yip?)2平均绝对值误差(L1损失):MAE=i=1∑n?∣yi??yip?∣...
传统神经网络:
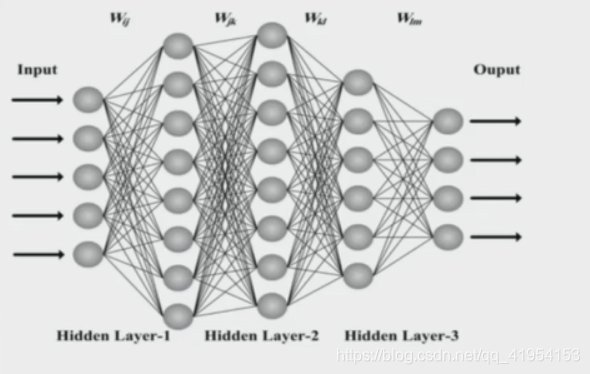
全连接网络处理图像的问题:
??参数过多:权重矩阵的参数太多 -> 过拟合
卷积神经网络的解决方式:
??局部关联,参数共享
基本组成结构
卷积
一维卷积
一维卷积经常用在信号处理中,用于计算信号的延迟积累
假设一个信号发生器在时刻t发出一个信号
x
t
x_t
xt?,其信息的衰减率为
f
k
f_k
fk?,即在k-1个时间步长后,信息衰减为原来的
f
k
f_k
fk?倍
设
f
1
=
1
,
f
2
=
1
2
,
f
3
=
1
4
f_1=1,f_2={1\over2},f_3={1\over4}
f1?=1,f2?=21?,f3?=41?在时刻t收到的信号
y
t
y_t
yt?为当前时刻产生的信息和以前时刻延迟信息的叠加
y
t
=
1
×
x
t
+
1
/
2
×
x
t
?
1
+
1
/
4
×
x
t
?
2
=
f
1
×
x
t
+
f
2
×
x
t
?
1
+
f
a
×
x
t
?
2
=
∑
k
=
1
3
f
k
?
x
t
?
k
+
1
y_t=1\times x_t+1/2 \times x_{t-1}+1/4 \times x_{t-2} \\ \quad =f_1 \times x_t+f_2 \times x_{t-1}+f_a \times x_{t-2} \\ \quad =\sum_{k=1}^3f_k \cdot x_{t-k+1}
yt?=1×xt?+1/2×xt?1?+1/4×xt?2?=f1?×xt?+f2?×xt?1?+fa?×xt?2?=k=1∑3?fk??xt?k+1?
此处的
f
=
f
[
f
1
,
f
2
,
f
3
]
f=f[f_1,f_2,f_3]
f=f[f1?,f2?,f3?]被称为滤波器(filter)或卷积核(convolutional kernel)
设滤波器f长度为m,它和一个信号序列x=[
x
1
,
x
2
,
x
3
,
.
.
.
x_1,x_2,x_3,...
x1?,x2?,x3?,...]的卷积记为:
y
t
=
∑
k
=
1
m
f
k
?
x
t
?
k
+
1
y_t=\sum_{k=1}^mf_k \cdot x_{t-k+1}
yt?=k=1∑m?fk??xt?k+1?
卷积是什么?
卷积是对两个实变函数的一种数学操作。
在图像处理中,图像是以二维矩阵的形式输入到神经网络的,因此我们需要二维卷积。
涉及到的基本概念?
input:输入
kernel/filter:卷积核/滤波器
weights:权重
receptive field:感受野
activation map或feature map:特征图
padding
depth/channel:深度
output:输出
更具体
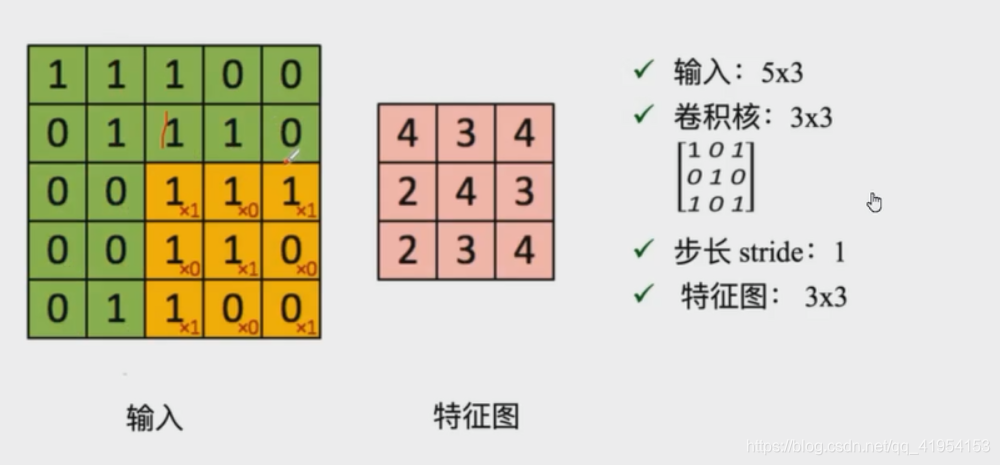
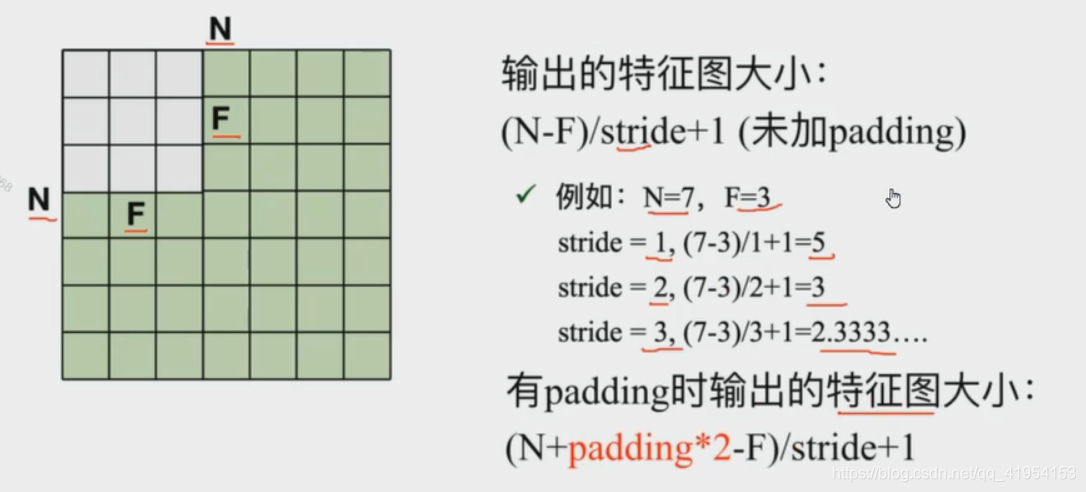
卷积核与输入对应卷积核大小窗口对应相乘后相加
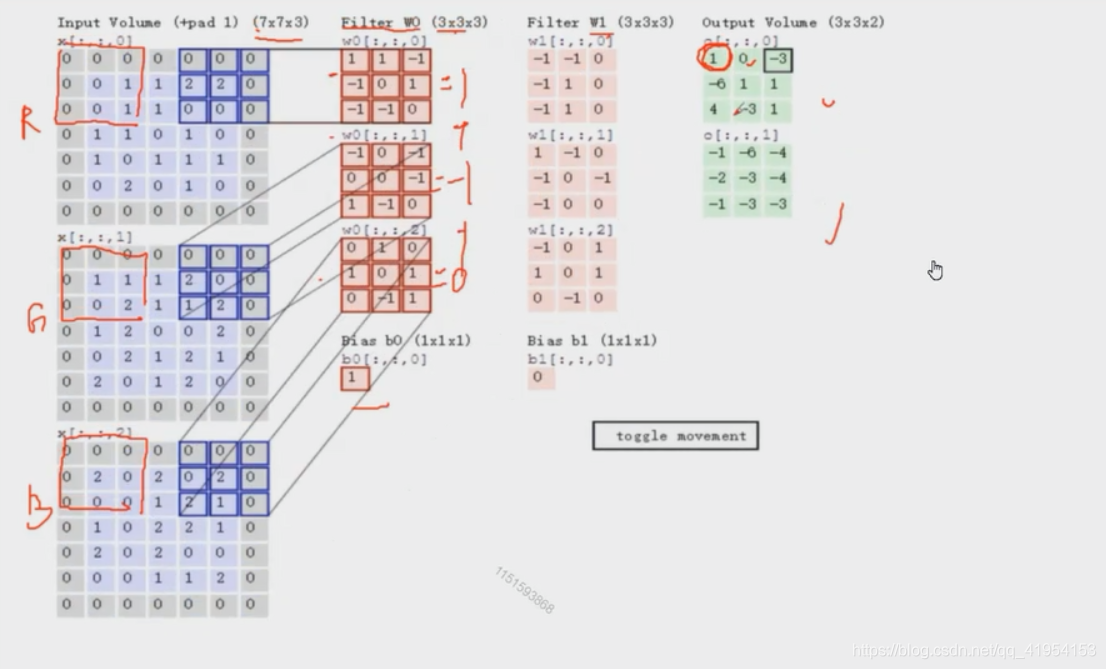
channel为3卷积核channel也为3,一个卷积核产生一个feature map
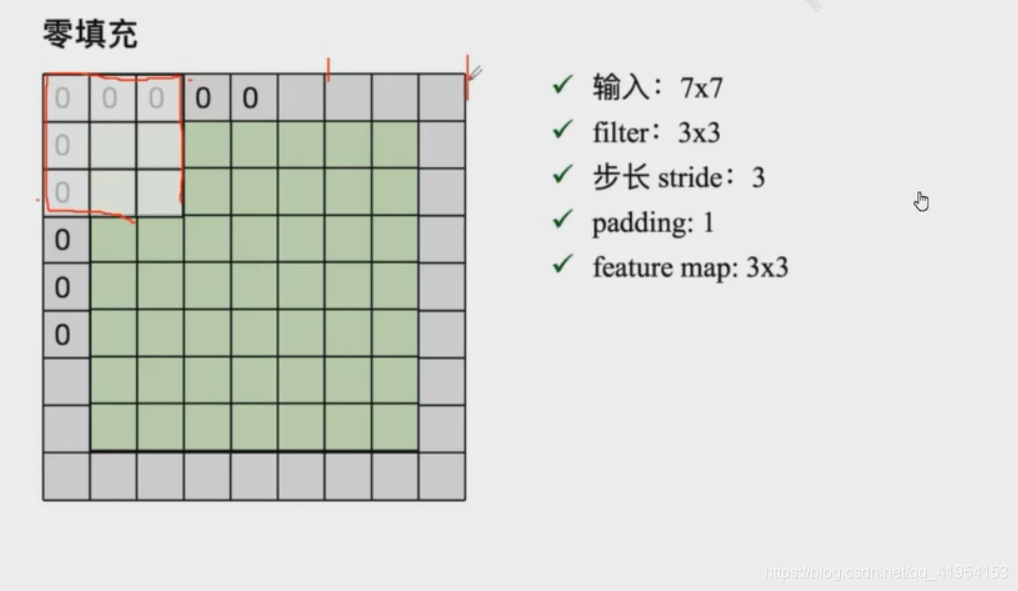
步长无法匹配输入需要进行填充
池化

Polling:
?? 保留了主要特征的同时减少参数和计算量,防止过拟合,提高模型泛化能力
??它一般处于卷积层与卷积层之间,全连接层与全连接层之间
Pooling的类型:
??Max pooling:最大值池化
??Average pooling:平均池化

全连接
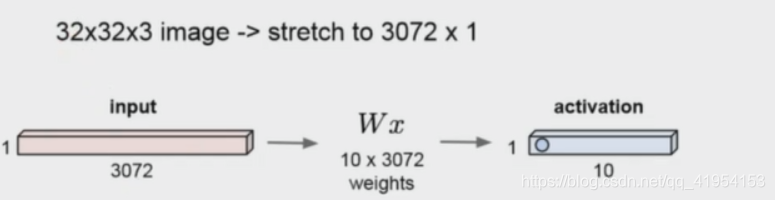
全连接层/FC layer:
两层之间所有神经元都有权重链接
通常全连接层在卷积神经网络尾部
全连接层参数量通常最大
一个典型的卷积网络是由卷积层、池化层、全连接层交叉堆叠而成