[人工智能]2021机器学习李宏毅-1

Regression

Machine Learning

? 机器具备有学习的能力，事实上，机器学习概括来说可以用一句话来描述机器学习这件事，机器学习就是让机器具备找一个函式的能力。

那机器具备找函式的能力以后,他确实可以做很多事 举例来说

• 语音辨识,函式的输入是声音讯号,输出是这段声音讯号的内容。我们期待凭藉著机器的力量,把这个函式自动找出来，这件事情,就是机器学习。
• 影像辨识，这个函式的输入是一张图片,他的输出是什麼呢？他是这个,图片裡面 有什麼样的内容。
• 甚至是大家都知道的AlphaGo,其实也可以看作是一个函式,函式的输入,是棋盘上黑子跟白子的位置, 输出是机器下一步,应该落子的位置。让机器可以学习自动下围棋,就可以做一个AlphaGo。

Different types of Functions

• Regression,Regression的意思是说,假设我们今天要找的函式,他的输出是一个数值,他的输出是一个 scalar,那这样子的机器学习的任务,我们称之為Regression(回归)。

? 预测未来某一个时间的PM2.5的数值，机器找一个函式,这个我们用f来表示,这个函式的输出,是明天中午的PM2.5的数值,他的输入可能是种种跟预测PM2.5,有关的指数,包括今天的PM2.5的数值,今天的平均温度,今天平均的臭氧浓度等等,这一个函式可以拿这些数值当作输入,输出明天中午的PM2.5的数值,那这一个找这个函式的任务,叫作Regression。
?

• Classification(分类),要机器做的是选择题 我们人类,先準备好一些选项 那这些选项,又叫作类别 又叫作classes,我们现在要找的函式它的输出,就是从我们设定好的选项裡面,选择一个当作输出 那这个问题,这个任务就叫作Classification。

? 垃圾邮件的侦测,这个函式的输入是一封电子邮件,那他的输出的可能的选项就是两个,是垃圾邮件 或不是垃圾邮件,Yes或者是No,那机器要从Yes跟No裡面,选一个选项出来,这个问题叫作Classification,那Classification不一定只有两个选项,也可以有多个选项 。

? alpha go本身也是一个Classification,的问题 那只是这个Classification,他的选项是比较多的,那如果要叫机器下围棋,你想做一个 alpha go的话,我们要给机器多少的选项呢,你就想想看 棋盘上有多少个位置,那我们知道棋盘上有19乘19个位置,那叫机器下围棋这个问题 其实,就是一个有19乘19个选项的选择题,你要叫机器做的就是找一个函式,这个函式的输入是棋盘上,黑子跟白子的位置,输出就是从19乘19个选项裡面,选出一个正确的选项,从19乘19个可以落子的位置裡面,选出下一步应该要落子的位置,那这个问题也是一个分类的问题。

? 除了Regression跟Classification以外,还有一个Structured Learning,也就是机器今天不只是要做选择题,不只是输出一个数字 还要产生一个有结构的物件。举例来说,机器画一张图 写一篇文章,这种叫机器產生有结构的东西的问题,就叫作Structured Learning,那如果要讲得比较拟人化,比较潮一点 Structured Learning,你可以用拟人化的讲法说,我就是要叫机器学会创造这件事情,好那到目前為止,我们就是讲了三个机器学习的任务,Regression Classification跟Structured Learning,

Case Study

预测youtube频道的观看人数，根据一个频道过往所有的资讯去预测,它明天有可能的观看的次数是多少呢,我们能不能够找一个函式,这个函式的输入是youtube上面的后台资讯,输出就是某一天,隔天这个频道会有的总观看的次数.

机器学习找这个函式的过程,分成三个步骤,那我们就用Youtube频道,点阅人数预测这件事情,来跟大家说明这三个步骤,是怎麼运作的

1. Function with Unknown Parameters

写出一个,带有未知参数的函式,简单来说就是 我们先猜测一下,我们打算找的这个函式$F$,它的数学式到底长什麼样子。举例来说,我们这边先做一个最初步的猜测,我们写成这个样子
$$y=b+w?x?$$

• $y$是我们准备要预测的东西，今天这个频道总共观看的人
• $x?$是这个频道,前一天总共观看的人数,$y$跟$x?$都是数值,
• b跟w是未知的参数,它是准备要通过资料去找出来的,我们还不知道w跟b应该是多少,我们只是隐约的猜测

这个猜测往往就来自於,你对这个问题本质上的了解,也就是Domain knowledge,所以才会听到有人说,这个做机器学习啊,就需要一些Domain knowledge,.

? 所以我们这个能够预测未来点阅次数的函式$F$,猜测今天的点阅次数会跟昨天的点阅次数有点关联,所以我们把昨天的点阅次数,乘上一个数值,再加上一个b做修正,当作是对今天点阅次数的预测,这是一个猜测,它不一定是对的,我们等一下回头会再来修正这个猜测。

? 那现在总之,我们就随便猜说,$y=b+w?x?$,而b跟w是未知的,这个带有未知的==参数,这个Parameter中文通常翻成参数,这个带有Unknown的Parameter的Function 我们就叫做Model,所以我们常常听到有人说Model,这个东西在机器学习里面,就是一个带有未知的Parameter的Function,
?
? 这个$x?$是这个Function里面我们已知的,来自Youtube后台的资讯,我们已经知道昨天的点阅的总人数是多少,这个东西叫做Feature==,而$w$跟$b$是我们不知道的,它是Unknown的Parameter,那这边我们也给$w$跟$b$,给他一个名字,这个跟Feature做相乘的未知的参数,这个w 我们叫它weight,这个没有跟Feature相乘的,是直接加下去的,这个我们叫它Bias,那这个只是一些名词的定义而已,等一下我们讲课的时候,我们在称呼,模型里面的每一个东西的时候,会更方便,好那这个是第一个步骤

2. Define Loss from Training Data

? 第二个步骤,是我们要定义一个东西叫做Loss,Loss它也是一个Function,那这个Function它的输入,是我们Model裡面的参数,我们的Model叫做,$y=b+w?x?$,而$b$跟$w$是未知的,Function的输入,就是$b$跟$w$,这个Function输出的值代表说,现在如果我们把这一组未知的参数,设定某一个数值的时候,这笔数值好还是不好。

? 假设现在我们给未知的参数的设定$w$是1,bias是0.5 k,用来预测未来的点阅次数，从训练资料来进行计算,在这个问题里面,我们的训练资料是一个频道过去的点阅次数,举例来说,从2017年到2020年的点阅次数,每天的这个频道的点阅次数都知道,所以那我们知道,2017年1月1号,到2020年12月31号的,点阅数字是多少,接下来我们就可以计算Loss。我们把2017年1月1号的点阅次数,代入这一个函式里面,我们已经说我们想要知道,b是0.5 k,$w$设定是1的时候,那我们就把这个$x_1$代4.8 k,看它的预测出来的结果是多少,那第二天应该是4.8 k乘1加0.5 k,就是5.3 k的点阅次数,我们比对一下,现在这个函式预估的结果,跟真正的结果,它的差距有多大,这个函式预估的结果是5.3 k,真正的结果是4.9 k,那这个真实的值叫做Label,它是高估了,高估了这个频道可能的点阅人数,那就可以计算一下估测的值,跟真实的值的差距,这边**估测的值用$y$来表示,真实的值用$\hat{y}$**来表示,你可以计算$y$跟$\hat{y}$之间的差距,得到一个$e_1$,二者相减算出来的值是0.4 k。

? 那这三年来每一天的误差,通通都可以算出来,每一天的误差都可以给我们一个小e,

? 接下来我们就把每一天的误差,通通加起来,加起来然后取得平均,这个N代表我们的训验资料的个数,就是三年来的训练资料,就365乘以3,每年365天 所以365乘以3,那我们算出一个L,这L是每一笔训练资料的误差,这个e相加以后的结果,这个L就是我们的Loss，==L越大,代表我们现在这一组参数越不好,这个大L越小,代表现在这一组参数越好。

$e=|y?\hat{y}|$，L is mean absolute error,缩写是MAE,

$e=(y?\hat{y}{)}^2$，L is mean square error,缩写是MSE,

有一些任务,都是机率分佈的话,选择Cross-entropy。

Error Surface，调整不同的b和w,组合起来以后,都去计算它的Loss,然后就可以画出以下这一个等高线图.

3. Optimization

? 找一个w跟b,把未知的参数,找一个数值出来,看代那一个数值进去,可以让我们的Loss的值最小,那个就是我们要找的w跟b,

Gradient Descent
当我们w代入不同的数值的时候,我们就会得到不同的Loss,这一条曲线就是error surface。

• 随机选取一个初始的点,那这个初始的点,我们叫做**$w?$**,假设我们随机决定的结果,是在$w_0$这个地方。

• 然后计算$\frac{?L}{?w}{|}_{w=w_0}$，如果为负，如上图的情况，那么$w$增加，Loss会变小。除了微分这一项,还有另外一个东西会影响步伐大小,这个东西我们这边用$\eta$来表示,这个$\eta$叫做learning rate,叫做学习速率,这个learning rate。它是怎麼来的呢,它是你自己设定的,你自己决定这个$\eta$的大小,如果$\eta$设大一点,那你每次参数update就会量大,你的学习可能就比较快,如果η设小一点,那你参数的update就很慢,每次只会改变一点点参数的数值,那这种你在做机器学习,需要自己设定的东西,叫做 hyperparameters

$$w^1\leftarrow w^0?\eta \frac{?L}{?w}|(w=w^0)$$
反复进行刚才的操作,你就计算一下$w^1$微分的结果,然后再决定现在要把$w^1$移动多少,然后再移动到$w^2$,然后你再继续做同样的操作,不断的把$w$移动位置,最后你会停下来.

训练完成

• 最开始设置的训练次数，我的上限就是设定100万次,就我参数更新100万次以后,我就不再更新了。

• 那还有另外一种理想上的,停下来的可能是,今天当我们不断调整参数,调整到一个地方,它的微分的值就是这一项,算出来正好是0的时候,如果这一项正好算出来是0,0乘上learning rate还是0,所以你的参数就不会再移动位置,那假设我们是这个理想的状况,我们把w?更新到w1,再更新到w2,最后更新到w?有点卡,w?卡住了,也就是算出来这个微分的值是0了,那参数的位置就不会再更新,

缺陷：可能没有找到真正最好的解,我们没有找到那个,可以让Loss最小的那个w,在这个例子裡面,把w设定在右侧红点附近这个地方,你可以让loss最小,但是如果 Gradient Descent,是从W⁰这个地方,当作随机初始的位置的话,也很有可能走到W^T这裡,你的训练就停住了,你就没有办法再移动w的位置。

那右侧红点这一个位置,这个真的可以让loss最小的地方,叫做global minima,而W^T这个地方叫做local minima,它的左右两边,都比这个地方的loss还要高一点,但是它不是整个error surface上面的最低点。如果自己做过Gradient Descent 经验的话,其实local minima是一个假问题,

? 刚才举的例子,是只有一个参数的例子而已,那实际上我们刚才的模型有两个参数,有w跟b,那有两个参数的情况下,如何用Gradient Descent呢？

• 我们现在有两个参数,都给它随机的初始的值,就是$w?$跟$b?$

• 你要计算w跟loss的微分
  $$\frac{?L}{?b}|(w=w^0,b=b^0)$$

  $$\frac{?L}{?w}|(w=w^0,b=b^0)$$

• 更新参数

  $$w^1\leftarrow w^0?\eta \frac{?L}{?w}|(w=w^0,b=b^0)$$

$$b^1\leftarrow b^0?\eta \frac{?L}{?b}|(w=w^0,b=b^0)$$

更新完得到$w^{?}$ 和 $b^{?}$.

更新参数的方向如图，把w跟b更新的方向结合起来,就是一个向量,就是这个红色的箭头,我们就从这个位置移到这个位置

Linear Model

• 横轴是代表的是时间,所以0这个点 最左边的点,代表的是2021年1月1号,最右边点,代表的是2021年2月14号

• 纵轴就是观看的人次,这边是用千人当作单位,

• 红色的线是真实的观看人次

• 蓝色的线是机器用这一个函式,预测出来的观看人次

  根据图中的数据，我们看出来每隔七天一个循环,每个礼拜五礼拜六,看的人就是特别少。所以既然我们已经知道每隔七天,就是一个循环,那这一个式子 这一个model,显然很烂,因为它只能够看前一天。每隔七天它一个循环,如果我们一个模型,它是参考前七天的资料,把七天前的资料,直接复制到拿来当作预测的结果,也许预测的会更准也说不定,所以我们就要修改一下我们的模型,通常一个模型的修改,往往来来自你对这个问题的理解,也就是Domain Knowledge。

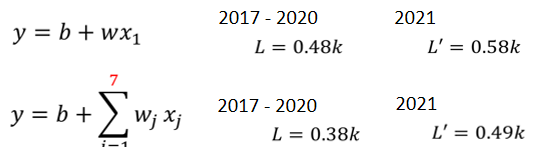
Regression P2

Piecewise Linear Curves

? 我们可以想像说 x1 跟 y,也许它中间有比较复杂的关係,对 Linear Model 来说,$x_1$跟$y$的关係就是一条直线, $x_1$越来越大,y就应该越来越大,设定不同的w和b,改变这一条蓝色的直线,跟 y 轴的交叉点,但是无论你怎么改w跟 b,它永远都是一条直线,永远都是$x_1$越大$y$越大，前一天观看的人数越多,隔天的观看人数就越多

? 但也许现实并不是这个样子

• 也许在$x_1$小于某一个数值的时候,前一天的观看人数跟隔天的观看人数是成正比,
• 也许当$x_1$大于一个数值的时候,这个物极必反。假设$x_1$很大,前天观看的人数太高,那隔天观看人数就会变少也说不定
• 也许$x_1$跟$y$中间,有一个比较复杂的,像这个红色线一样的关系

? 但你不管怎么设置w 跟 b,无法用 Linear Model制造出红色那一条线,显然 Linear Model 有很大的限制, 叫做**Model 的 Bias**,

? 所以我们需要写一个更复杂的,更有弹性的,有未知参数的 Function,

? 我们可以观察一下红色的这一条曲线,它可以看作是一个常数,再加上一群蓝色的这样子的 Function,.

这个蓝色的 Function,它的特性是

• 当输入的值,当 x 轴的值小于某一个这个 Flash Hold 的时候,它是某一个定值,
• 大于另外一个 Flash Hold 的时候,又是另外一个定值,
• 中间有一个斜坡

? 那怎麼加上这个蓝色的 Function 以后,变成红色的这一条线?

? 所以红色这个线,可以看作是一个常数,再加上一堆蓝色的 Function

? 你现在这个 Curves 啊,它是有很多线段所组成的,它是有很多锯齿状的线段所组成的,这个叫做 Piecewise Linear 的 Curves,那你会发现说这些 Piecewise Linear 的 Curves,你有办法用常数项,加一大堆的蓝色 Function 组合出来,只是他们用的蓝色 Function 不见得一样,你要有很多不一样的蓝色 Function,加上一个常数以后,你就可以组出这些 Piecewise Linear 的 Curves。那如果你今天 Piecewise Linear 的 Curves 越复杂,也就是这个转折的点越多啊,那你需要的这个蓝色的 Function 就越多

? 如果是这样的曲线，在这样的曲线上面,先取一些点,再把这些点点起来,变成一个 Piecewise Linear 的 Curves,而这个 Piecewise Linear 的 Curves 跟原来的曲线,它会非常接近,如果你今天点取的够多,或你点取的位置适当的话,这个 Piecewise Linear 的 Curves,就可以逼近这一个,连续的这一个曲线,就可以逼近这一个不是 Piecewise Linear,它是有角度的 有弧度的这一条曲线。

? 所以我们今天知道一件事情,你可以用 Piecewise Linear 的 Curves,去逼近任何的连续的曲线,而每一个 Piecewise Linear 的 Curves,又都可以用一大堆蓝色的 Function 组合起来,也就是说,我只要有足够的蓝色 Function 把它加起来,我也许就可以变成任何连续的曲线

? 所以今天,假设我们的 x 跟 y 的关係,它也许非常地复杂,那也没关係,我们就想办法写一个带有未知数的 Function,这个带有未知数的 Function 它表示的,就是一堆蓝色的 Function,加上一个 Constant,那我们接下来要问的问题就是,这一个蓝色 Function,它的式子应该要怎麼把它写出来呢？

曲线的表达形式，函数式子
$$y=c\frac{1}{1+e^{?(b+w{x}_1)}}$$

• $x_1$趋近于无穷大的,那 $e^{?(b+w{x}_1)}$趋近于0,$y$趋近于c
• $x_1$趋近于无穷小的,那 $e^{?(b+w{x}_1)}$趋近于无穷,$y$趋近于0

$$y=c?sigmoid(b+w{x}_1)$$

sigmoid的函数特性

• 如果你今天改 $w$ 你就会改变斜率你就会改变斜坡的坡度
• 如果你动了 $b $ 你就可以把这一个 Sigmoid Function 左右移动
• 如果你改 $c$ 你就可以改变它的高度

? 所以你只要有不同的 w 不同的 b 不同的 c,你就可以制造出不同的 Sigmoid Function,把不同的 Sigmoid Function 叠起来以后,你就可以去逼近各种不同的,Piecewise Linear 的 Function,然后 Piecewise Linear 的 Function,可以拿来近似各种不同的 Continuous 的 Function

? 所以假设我们要把红色的这条线，函数式子。

$$y=b+\sum _i{c}_{i}sigmoid(b_i+w_i{x}_1)$$

? 减少 Model 的 Bias ，我们可以写一个更有弹性的,有未知参数的 Function,它叫做 $y=b+{\sum }_i{c}_{i}sigmoid(b_i+w_i{x}_1)$ 本来这边是 $b+w{x}_1$,这边变成$b_i+w_i{x}_1$,我们只要带入不同的 c 不同的 b 不同的 w,我们就可以变出各式各样,就可以组合出各式各样不同的 Function

? 我们先考虑一下j是1、2、3

? 这个得到的式子就是这个样子,所以这边我们用 $w_{ij}$ ,来代表在第 i 个 Sigmoid 里面,乘给第 j 个 Feature 的 Weight,第一个 Feature 它就是 w11,第二个 Features 就是乘 w12,第三个 Feature 都是乘 w13,所以三个 Features1 2 3,这个 w 的第二个下标就是 123,w 的第一个下标代表是,现在在考虑的是第一个 Sigmoid Function,那我们有三个 Sigmoid Function,

矩阵相乘的方法来表示：

矩阵相乘的简化表示:

? 那把它改成线性代数比较常用的表示方式,x 乘上矩阵 w 再加上向量 b,会得到一个向量叫做 r,表示向量式。

?

整个过程的表达式：

? 重新定义一下我们的未知参数,

统称我们所有的未知的参数,我们就一律统称 $\theta$

loss from training data

? 我们现在的 Loss Function 就变成 $L(\theta )$

? 这个 Loss Function 要问的就是,这个 θ 如果它是某一组数值的话,会有多不好或有多好,那计算的方法和之前的相同。所有的误差通通加起来,你就得到你的 Loss

Optimization

? $\theta$表示成${\theta }_1$、${\theta }_2、$${\theta }_3$等等,找一组$\theta$使Loss 越小越好。可以让 Loss 最小的那一组 $\theta$, ${\theta }^{?}=argminL$

参数更新的过程。

数据训练的过程：

数据训练过程的中的概念定义：

?

• Epoch：所有训练样本都已输入到模型中，称为一个Epoch

• Batchsize： 批大小，决定一个Epoch有多少个batch

##激活函数

? 这个 Hard 的 Sigmoid,我刚才说它的函式有点难写出来,其实也没有那麼难写出来,它可以看作是两个 Rectified Linear Unit 的加总,所谓 Rectified Linear Unit 它就是长这个样

? 它有一个水平的线,走到某个地方有一个转折的点,然后变成一个斜坡,那这种 Function 它的式子,写成
$$c?max(0,b+w{x}_1)$$
? 每条不同的 w 不同的 b 不同的 c,你就可以挪动它的位置,你就可以改变这条线的斜率,那这种线呢在机器学习裡面,我们叫做 Rectified Linear Unit,它的缩写叫做 ReLU,名字念起来蛮有趣的,它真的就念ReLU

? 那你把两个 ReLU 叠起来,就可以变成 Hard 的 Sigmoid,你想要用 ReLU 的话,就把 Sigmoid 的地方,换成$ max(0, b_i + w_i{_j}x_j)$。

? 表示一个 Hard 的 Sigmoid,表示那个蓝色的 Function 不是只有一种做法,你完全可以用其他的做法,好 那这个 Sigmoid 或是 ReLU,他们在机器学习裡面,我们就叫它 Activation Function,他们是有名字的,他们统称为Activation Function.

? 当然还有其他常见的,还有其他的 Activation Function,但 Sigmoid 跟 ReLU,应该是今天最常见的 Activation Function,那哪一种比较好呢,这个我们下次再讲,哪一种比较好呢,我接下来的实验都选择用了 ReLU,显然 ReLU 比较好。

? 根据真实的数据进行试验：

?

? 继续改我们的模型，通过如下图的试验。

? 每次都加 100 个 ReLU,那我们就是 Imput Features,就是 56 天前的资料

• 如果是只做一次，就那个乘上 w 再加 b,再通过 ReLU 或 Sigmoid,这件事只做一次的话,这是我们刚才看到的结果
• 两次，这个 Loss 降低很多,0.28k 降到 0.18k,没看过的资料上也好了一些
• 三层，又有进步,从 0.18k 降到 0.14k,所以从一层到 从就是乘一次 w,到通过一次 ReLU,到通过三次 ReLU,我们可以从 0.28k 到 0.14k,在训练资料上,在没看过的资料上,从 0.43k 降到了 0.38k,看起来也是有一点进步的,

? 那这个是那个真实的实验结果啦,就我们来看一下,今天有做通过三次 ReLU 的时候,做出来的结果怎麼样

? 横轴就是时间,纵轴是观看的人次 是千人,红色的线代表的是真实的数据,蓝色的线是预测出来的数据

? 那你会发现说,在这种低点的地方啊,你看红色的数据是每隔一段时间,就会有两天的低点,在低点的地方,机器的预测还算是蛮準确的,那这边有一个神奇的事情,这个机器高估了真实的观看人次,尤其是在这一天,这一天有一个很明显的低谷,但是机器没有预测到这一天有明显的低谷,它是晚一天才预测出低谷。这天最低点就是除夕啊,谁除夕还学机器学习 对不对,好 所以当然对机器来说,你不能怪它,它根本不知道除夕是什麼,它只知道看前 56 天的值,来预测下一天会发生什麼事,所以它不知道那一天是除夕,所以你不能怪它预测地不准,这一天就是除夕。

Deep Learning

? Sigmoid 或 ReLU,它们叫做 Neuron,我们这边有很多的 Neuron,很多的 Neuron 就叫做 Neural Network。每一排 Neural 我们就叫它一个 Layer,它们叫 Hidden Layer,有很多的 Hidden Layer 就叫做 Deep,这整套技术就叫做 Deep Learning

? 就是这样来的,好 所以人们就开始,把类神经网路越叠越多 越叠越深,12 年的时候有一个 AlexNet,它有 8 层 它的错误率是 16.4%,两年之后 VGG 19层,错误率在影像辨识上进步到 7.3 %,这个都是在影像辨识上一个,这个基準的资料库上面的结果,后来 GoogleNet 有错误率降到 6.7%,有 22 层。

? Residual Net 有 152 层啊,它比 101 还要高啊。我们想要用 ReLU 或者是 Sigmoid,去逼近一个复杂的 Function,实际上只要够多的 ReLU 够多的 Sigmoid,就可以逼近任何的 连续的 Function ,我们只要有够多的 Sigmoid,就可以知道够复杂的线段,就可以逼近任何的 Continuous Function,所以我们只要一排 ReLU 一排 Sigmoid,够多就足够了。

? Network为4层的情况：

? 4 层在训练资料上的 Loss 是 0.1k,在没有看过 2021 年的资料上,是如何呢 是 0.44k。在训练资料上,3 层比 4 层差,但是在没看过的资料上,4 层比较差,3 层比较好。这种训练资料跟没看过的资料造成的结果不一致的状况,这个状况叫做 Overfitting,机器学习会发生 Overfitting 的问题,指的就是在训练资料上有变好,但是在没看过的资料上没有变好这件事情。