文章目录
一、为什么模型评估
(1)经验误差和泛化误差
经验误差:就是训练误差,在训练集上训练的误差。
泛化误差:测试集上的误差,训练后的模型在测试集上的误差。
(2)过拟合、欠拟合
过拟合:当学习器把训练样本学得太好的时候,很可能已经把训练样本自身的一些特点当做了所有潜在样本都会具有的一般性质,这样就会冬至泛化性能下降,这种状态叫过拟合。
欠拟合:与之相反则是欠拟合。
(3)多种因素导致过拟合、欠拟合以及相关解决方案
常见的就是 学习能力过于强大,以至于把训练样本所包含的不太一般的特性都学到了。而欠拟合通常由于学习能力低导致。
造成过拟合原因主要有以下几种:
- 训练数据集样本单一,样本不足。
- 训练数据中噪声干扰过大。
- 模型过于复杂。
解决过拟合的一些方法:
- 获取和使用更多的数据,增加数据的丰富性和多样性。
- 使用合适的网络模型。
- 提取的数据特征不易过多。
- 使用正则化项。
解决欠拟合的方法:
- 增加网络模型的复杂度和增加数据特征的提取。
- 增加训练代数。
- 决策树中扩展分支。
二、什么是模型评估
(1)评估方法
- 留出法
把数据集进行分割,大部分用以训练,少部分用于测试。 - 交叉验证法
把数据平均分成K份,K-1用以训练,单独的一份用以测试,分别做K次取平均值。 - 自助法
以上的方法都不能做到拿所有的训练集用以训练,而自助法是通过取出放回的方法,独立的取K次。用于训练,总有没取到的数据用以测试。
(2)性能度量
错误率、精度、查准率、查全率
True positives(TP,真正) : 预测为正,实际为正
True negatives(TN,真负):预测为负,实际为负
False positives(FP,假正): 预测为正,实际为负
False negatives(FN,假负):预测为负,实际为正
- 查询率 P = TP / TP + FP =预测结果为正的结果中,有多少是真正的预测对了
- 查全率 R = TP / TP + FN = 所有真值为正的数据中,有多少被真正预测对了
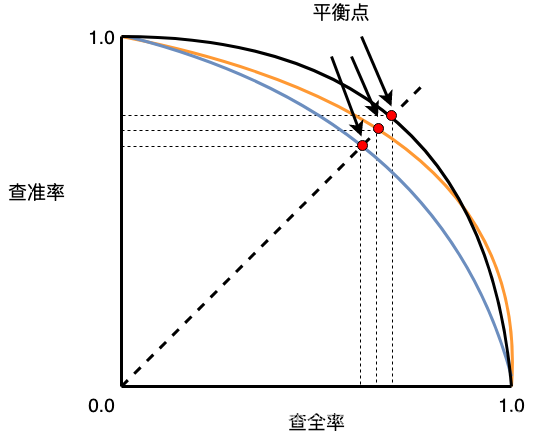
- Y轴为查准率 P,X 轴为查全率 R,呈现的就是 P-R 曲线。
- 平衡点大 ,模型性能好。
均方误差、ROC、AUC
-
均方误差:在预测任务中,我们通过训练得到对应的模型 f f f,然后通过模型去进行预测,得到的预测值 f ( x i ) f(x_{i}) f(xi?) 和真值 y i y_{i} yi? 进行比较,来评估模型的性能。
公式如下:
E ( f ; D ) ) = 1 m ∑ i = 1 m ( f ( x i ) ? y i ) 2 ) E(f;D))=\frac{1}{m}\sum_{i=1}^{m}(f(x_{i})-y_{i})^{2}) E(f;D))=m1?i=1∑m?(f(xi?)?yi?)2)
最小二乘法
均方误差具有很好的几何意义,它对应了常用的欧几里得距离,基于均方误差最小化来进行模型求解的方法称为 ‘最小二乘法’。
在线性回归中,最小二乘法就是试图找到一条直线,使所有样本到直线上的欧氏距离之和最小。
LDA(Linear Discriminant Analysis) 线性判别分析
LDA 的思想非常朴素:给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离;
在对新样本进行分类的时候,将其投影到同样的这条直线上,再根据投影点的位置来确定新样本的类别。
-
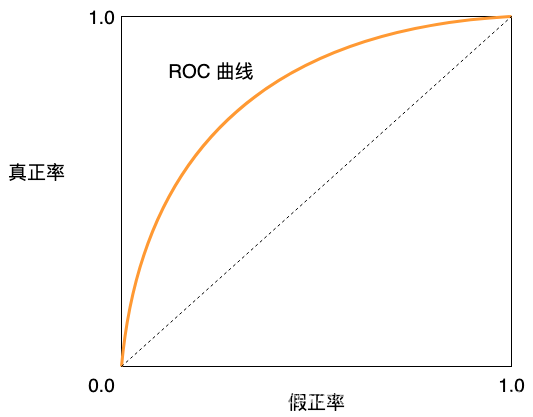
ROC
真正例率 TPR = TP / TP + FN = 所有正例中,有多少预测对了,也就是正样本预测精度
假正例率 FPR = FP / TN + FP = 所有负例中,有多少预测对是错的,也就是负样本预测精度
-
AUC (Area Under ROC Curve)
ROC 曲线下边的面积就是 AUC