[人工智能]时空图神经网络阅读笔记

STGCN

摘要

传统方法无法实现精确的中长期预测，忽视时空相关性。我们提出了一种新颖的时空图卷积网络，采用了全卷积结构。

方法

图卷积：GCN

时间卷积：卷积核在时间维度上滑动，对于长度为$M$的序列和宽度为$K_t$的卷积核，输出长度为$M?K_t+1$，最后使用了门控机制GLU
$$T{?}_{\tau }Y=P\odot \sigma (Q)$$
P和Q是使用不同参数的时间卷积的输出。

模型：

中间的是时空卷积块，两个时间卷积中间夹了图卷积，应用了瓶颈策略：图卷积的通道数很少，减少计算量

每一个时空卷积块后使用了layer normalization，对结点和特征做归一化。

第$l$个时空卷积块，对于输入$v^l\in R^{M\times n\times C^l}$，输出$v^{l+1}\in R^{(M?2(K_t?1))\times n\times C^{l+1}}$
$$v^{l+1}={\Gamma }_1^l{?}_{\tau }ReLU({\Theta }^l{?}_G({\Gamma }_0^l{?}_{\tau }{v}^l))$$
${\Gamma }_0^l$和${\Gamma }_1^l$分别是上面和下面的时间卷积核，${\Theta }^l$是图卷积核，在最后一个时空卷积块的后面附加了一个时间卷积层，将时间维度变为1，最后使用全连接层，实现单步预测

DCRNN

摘要

交通预测存在3个挑战：(1)路网上复杂的空间相关性，(2)非线性时间相关性，以及持续变化的路况，(3)实现长期预测的固有困难。我们将交通流建模成有向图上的扩散过程，提出了DCRNN。

方法

空间：扩散卷积，看作在图上的随机游走，经过多步后这个马尔可夫过程收敛到平稳分布，这里取K次迭代
$$X_{:,p}{?}_G{f}_{\theta }=\sum _{k=0}^{K?1}({\theta }_{k,1}(D_O^{?1}W{)}^k+{\theta }_{k,2}(D_I^{?1}{W}^T{)}^k)X_{:,p}$$
$D_O^{?1}W$和$D_I^{?1}{W}^T$分别表示前向和后向转移矩阵。扩展到多输出就是
$$H_{:,q}=a(\sum _{p=1}^P{X}_{:,p}{?}_G{f}_{{\Theta }_{q,p,:,:}})$$
$\Theta \in R^{Q\times P\times K\times 2}$，从P维映射到Q维。

时间：用扩散卷积替换GRU中的矩阵乘法

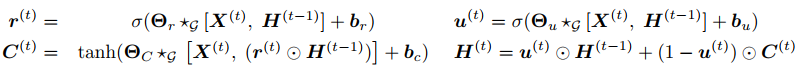
采用Endoder-Decoder结构进行多步预测，Decoder训练时输入真实值，预测时输入预测值，为了防止这种差异影响模型的性能，采用了Scheduled Sampling技术。

Graph WaveNet

摘要

现有的时空图建模方法都假设图结构是固定的，由于连接不完整，可能并没有反映真正的依赖关系，这些方法中使用的RNN和CNN不能捕获长期依赖。本文使用自适应邻接矩阵提取隐藏的空间依赖，使用堆叠的1维空洞卷积：感受野随层数指数增长，能够处理十分长的序列。

方法

图卷积：
$$Z=\sum _{k=0}^K{P}_f^{k}X{W}_{k1}+P_b^{k}X{W}_{k2}+{\tilde{A}}_{apt}^{k}X{W}_{K3}$$
$P_f$为归一化后的邻接矩阵 ，$P_b$是邻接矩阵的转置的归一化，分别代表前向转移矩阵和后向转移矩阵，${\tilde{A}}_{apt}$是自适应邻接矩阵
$${\tilde{A}}_{apt}=Softmax(ReLU(E_1{E}_2^T))$$
$E_1,E_2\in R^{N\times c}$为结点嵌入矩阵，$E_1$是源结点嵌入，$E_2$是目标结点嵌入。

时间卷积：带门控机制的一维因果卷积(GLU)，采用了空洞卷积。
$$h=g({\Theta }_1?X+b)\odot \sigma ({\Theta }_2?X+b)$$
模型：实验时共8层，空洞率为[1,2,1,2,1,2,1,2]：

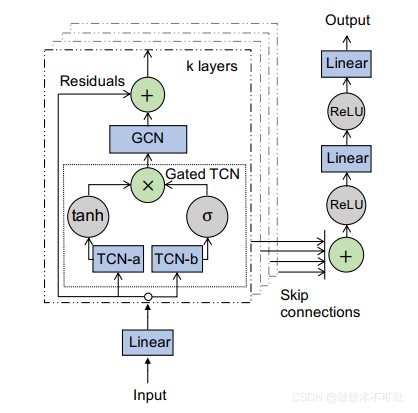
人工设计感受野大小，使最后一层时空卷积层输出的时间维度为1，经全连接层映射为输出维度

ASTGCN

待更新