[人工智能]深度学习算法-KNN聚类的原理和实现

K近邻算法：给定一个训练数据集，对新的的输入实例，在训练数据集中找到与该实例最邻近的的K个实例，这K个实例的多数属于某个类，就把该实例分为这个类。

K值选择、距离度量、以及分类决策(一般多数表决)为K近邻算法的三个基本要素。

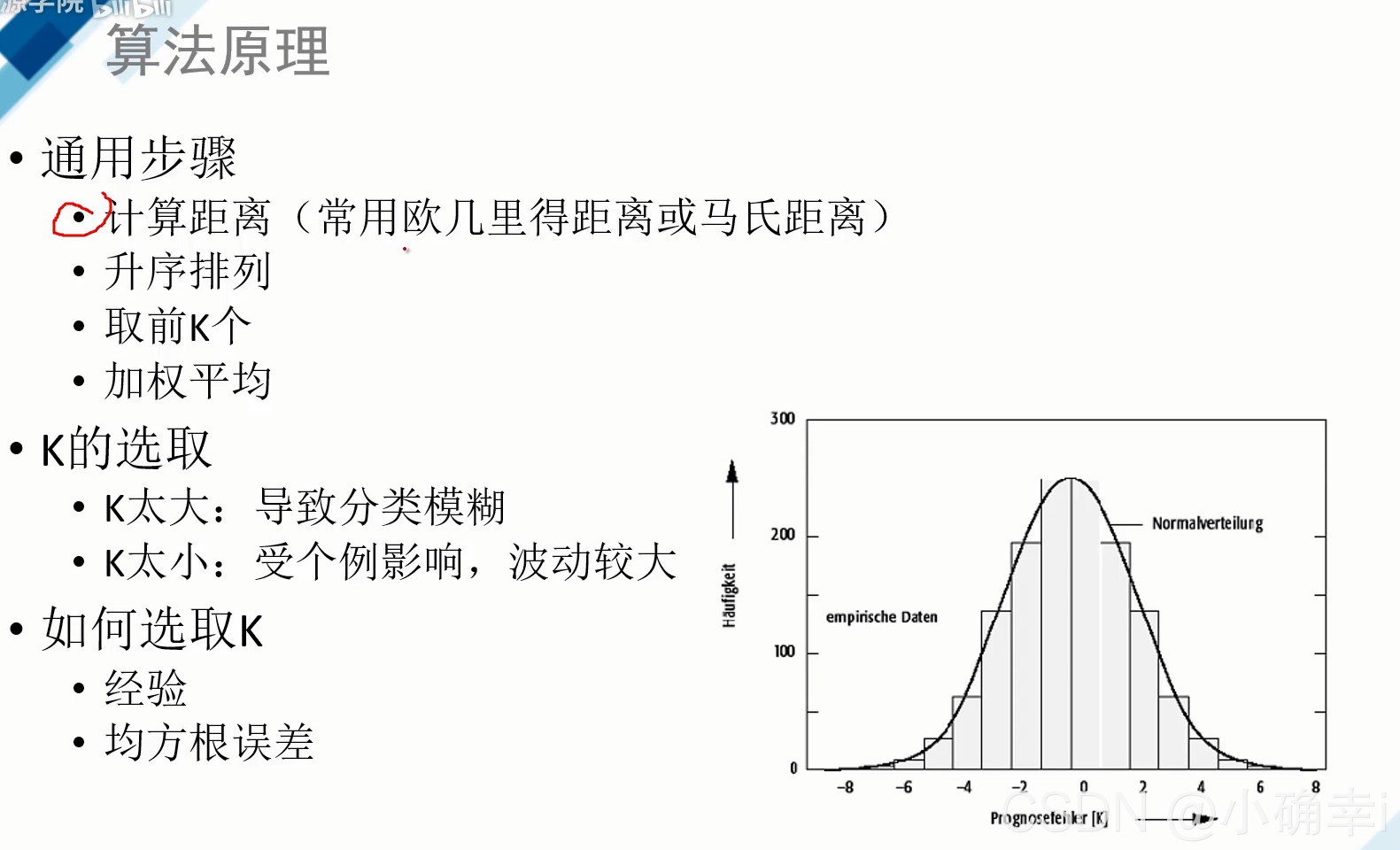
K值选择:

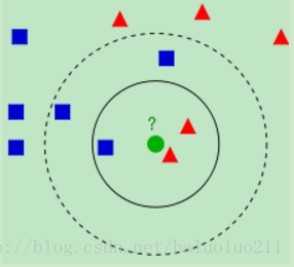
从上图中我们可以看到，图中的有两个类型的样本数据，一类是蓝色的正方形，另一类是红色的三角形。而那个绿色的圆形是我们待分类的数据。

如果K=3，那么离绿色点最近的有2个红色三角形和1个蓝色的正方形，这3个点投票，于是绿色的这个待分类点属于红色的三角形。
如果K=5，那么离绿色点最近的有2个红色三角形和3个蓝色的正方形，这5个点投票，于是绿色的这个待分类点属于蓝色的正方形。

可见K值的选择对分类的结果还是有很大的影响。

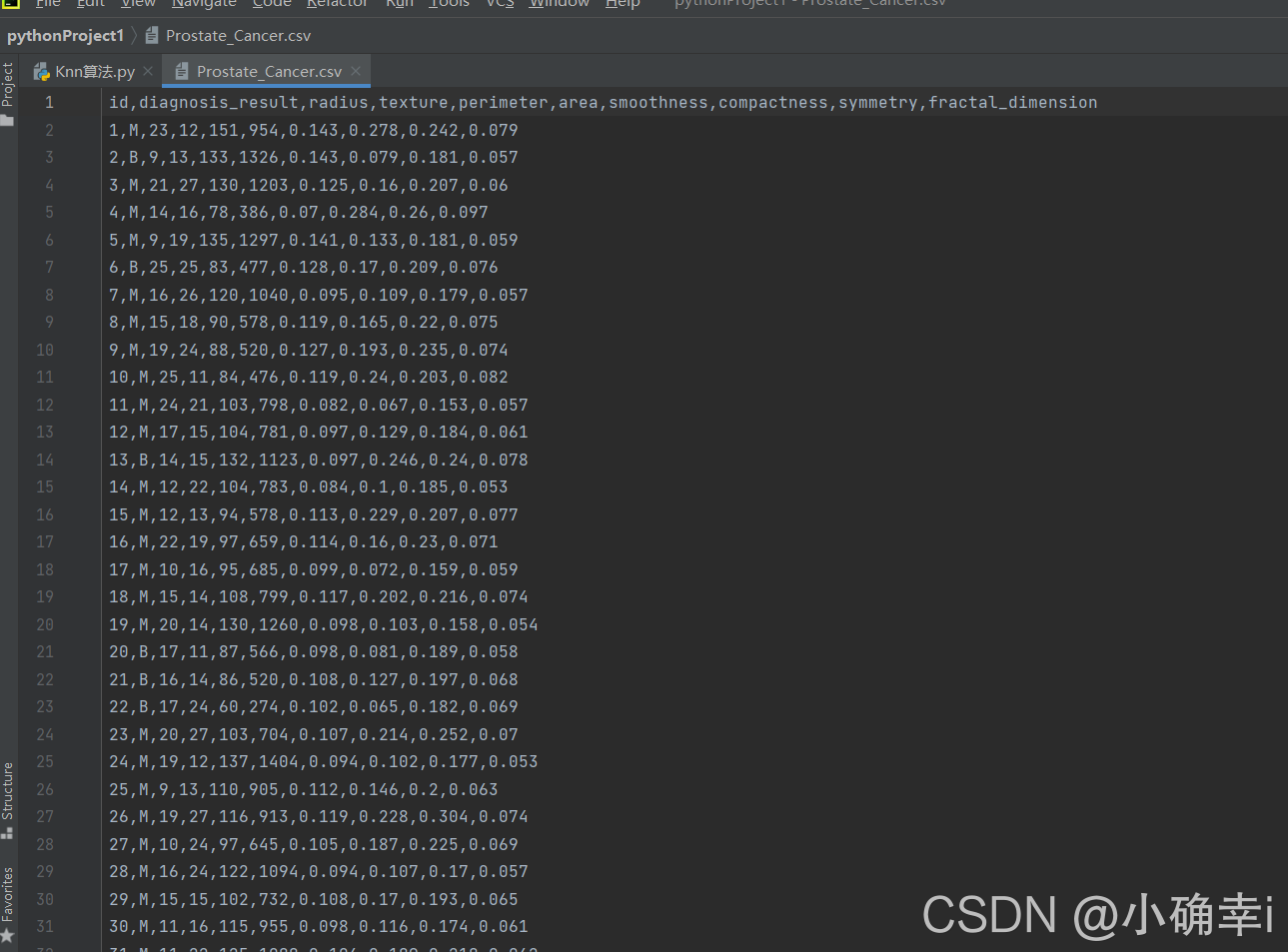
数据集

?

?测试代码

import random
import csv

# 读取
with open('Prostate_Cancer.csv', 'r') as file:
    reader = csv.DictReader(file)
    datas = [row for row in reader]

# 分组
random.shuffle(datas)
n = len(datas) // 3

test_set = datas[0:n]
train_set = datas[n:]


# KNN
# 距离
def distance(d1, d2):
    res = 0

    for key in ("radius", "texture", "perimeter", "area", "smoothness", "compactness", "symmetry", "fractal_dimension"):
        res += (float(d1[key]) - float(d2[key])) ** 2

    return res ** 0.5


K = 5


def knn(data):
    # 1.距离
    res = [
        {"result": train['diagnosis_result'], "distance": distance(data, train)}
        for train in train_set
    ]

    # 2.排序-升序
    res = sorted(res, key=lambda item: item['distance'])

    # 3.取前K个
    res2 = res[0:K]

    # 4.加权平均
    result = {'B': 0, 'M': 0}

    # 总距离
    sum = 0
    for r in res2:
        sum += r['distance']

    for r in res2:
        result[r['result']] += 1 - r['distance'] / sum

    if result['B'] > result['M']:
        return 'B'
    else:
        return 'M'


# 测试阶段
correct = 0
for test in test_set:
    result = test['diagnosis_result']
    result2 = knn(test)

    if result==result2:
        correct+=1

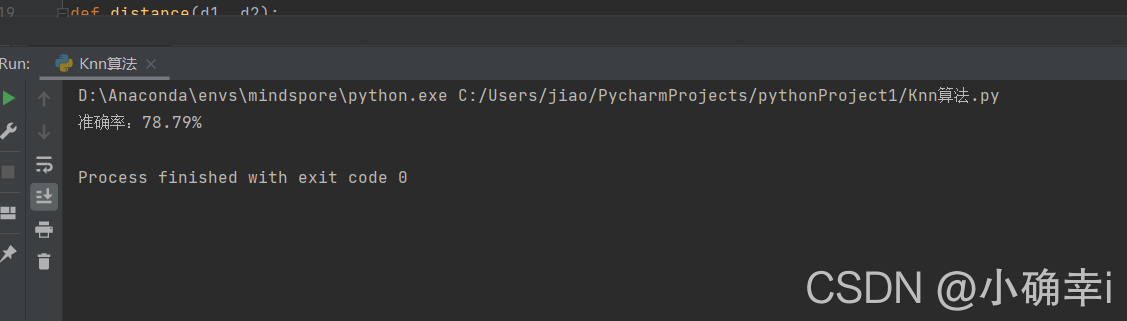
print("准确率：{:.2f}%".format(100*correct/len(test_set)))

测试结果

?