[人工智能]【深度学习浅尝】web自动化测试中识别图片算术验证码

本文参考实验楼课程：Python实现深度神经网络。

声明

我也是机器学习零基础，在本次实践中，仅仅是个人对机器学习的理解，由于水平有限，难免存在不对之处。因此对机器学习中涉及到的原理和概念还是建议参考原教程或者其他网络资源。当然，如果读者愿意就本文中涉及到的机器学习概念，算法等内容讨论，那也是非常欢迎的~

背景

项目自动化测试时，登录界面需要输入验证码。以前主要有两种做法：

1. 调用第三方接口识别
2. 请开发GG注释掉验证码

显然，方案1费钱且识别率无法控制，方案二费事，需要线上/测试来回切换。本文介绍第三种方法。利用深度学习识别图片验证码。效果如下：
截图1：验证码输入正确成功登陆及验证码输入错误登录失败

截图2：准确度测试。400个数据用于训练，200个数据用于预测精确度。在600轮迭代下，准确度高达90%（经实测，如果增大迭代轮数，准确度可高达98%）。准确度和训练/预测样本，迭代轮数，随机初始值有关。

深度学习概念

神经网络

神经网络结构如下：

这是一个两层的简单神经网络结构。一个圆圈称谓神经元。a1 ~ a3为网络层1，b1 ~ b2为网络层2。神经元之间通过直线相连，并有权重w。

网络层1和2之间是线性计算，公式如下：
$w11?al+w12?a2+w13?a3+bias1=b1$
$w21?al+w22?a2+w23?a3+bias2=b2$

网络层2和最终输出之间是非线性计算（该函数又称为sigmod函数，激活函数），公式如下：
$$h=\frac{1}{1+e^{?b}}$$

sigmoid函数图像如下，它的函数值总是介于0~1之间，表示预测结果Y等于1的概率。如：当Y=0.4时，那么Y=1的概率为0.4，也就是说Y更有可能等于0（此处的Y等于1还是0表示分类的概念）.

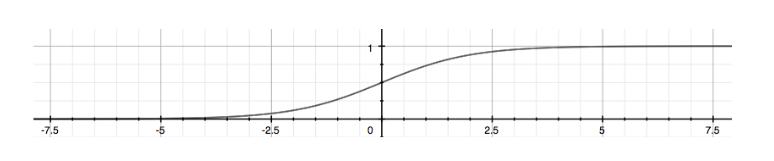
综上，该神经网络层最终的计算公式如下：
$$y=sigmoid(wx+b)$$

损失函数

二次损失函数

二次损失函数是最常见的一种，计算方式如下：
$$J({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x_i)?y_i{)}^2$$
我们已经有了训练数据，也就是已经有了$x_i$和$y_i$，现在的目的就是不断调整参数$\theta$，从而使损失函数值最小。图形上直观理解就是：尽可能使这个model拟合已有训练数据。
二次损失函数常用于回归问题

交叉熵损失函数

对于分类问题，交叉熵损失函数比二次损失函数更适用。公式如下：
$$J(\theta )=?\frac{1}{m}(ylog(h_{\theta }(x))+(1?y)log(1?h_{\theta }(x)))$$
至于原因，涉及较为复杂的数学知识。大概是因为交叉熵函数的导数 * 激活层sigmoid的导数可以刚好抵消掉sigmoid(x)*(1-sigmoid(x))这一部分计算。从而解决深度学习中梯度消失的问题。

梯度消失：也就是迭代多轮，我们算法的学习效果不明显，无法快速找到损失函数的最低值。这是因为在梯度下降算法中${\theta }_j:={\theta }_j?\alpha \frac{\delta }{\delta {\theta }_j}J(\theta )$，$\alpha \frac{\delta }{\delta {\theta }_j}J(\theta )$的值中的一个因子是sigmoid函数的导数$y^{\prime }$，$y^{\prime }=sigmoid(x)?(1?sigmoid(x))$,当x=0，$y^{\prime }$有最大值0.25，当x为其他值时，$y^{\prime }$的值急剧减小。当存在多层网络层时，该值多次相乘会使结果进一步变小，也就是每次参数变化的步长过小，从而产生梯度消失的问题。

详见文首实验楼教程中的最后一章的最后一节。部分截图如下：


交叉熵损失函数的导数为：（很久木有用数学了，不做推导，直接抄公式）：
$$y^{\prime }=\frac{h_{\theta }(x)?y}{h_{\theta }(x)?(1?h_{\theta }(x))}$$

梯度下降算法

假设$h_{\theta }(x)={\theta }_0+{\theta }_1?x_1$，那么损失函数的图像如下：

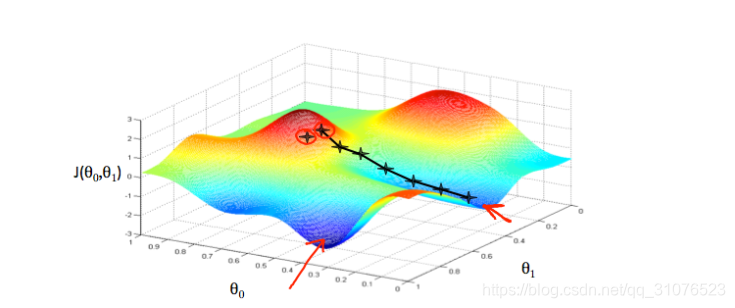
可以在三维空间想象，从任意一个初始点（${\theta }_0,{\theta }_1$），现在想要走到局部最低点，那么就根据该点的斜率，走到局部最低点即可。不同的初始点可能会得到不同的路径。每步走的大小称为学习速率α。公式如下：
$${\theta }_j:={\theta }_j?\alpha \frac{\delta }{\delta {\theta }_j}J({\theta }_0,{\theta }_1)$$

$\frac{\delta }{\delta {\theta }_j}J({\theta }_0,{\theta }_1)$称为偏导数，实际和导数、斜率没多大区别，单个变量叫导数，现在有多个变量（${\theta }_0,{\theta }_1$）就称为偏导数。
对于上述梯度算法的理解，针对单个变量，可看下图：

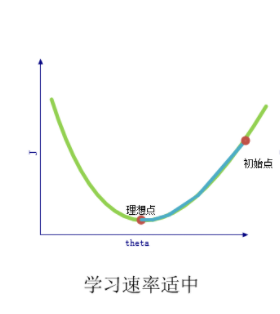
初始点的导数为正，即$d_{{\theta }_0}>0$，那么${\theta }_0={\theta }_0?\alpha ?d_{{\theta }_0}$得到一个比${\theta }_0$更小的数，下轮迭代将使即${\theta }_0$左移；同理可得，当导数为负，即$d_{{\theta }_0}<0$时，下轮迭代将使即${\theta }_0$右移。无论初始点在哪儿怎样，按照此梯度下降算法，经过一定轮次的迭代，我们终将找到局部最优解（即理想点）。

学习速率α的选择要适中，由上述内容很容易分析出下面的结论：

α太小，梯度下降算法需要迭代很多次才能达到最优解
α太大，某步可能超过最优解，从而越来越偏离最优解

学习速率过大的情况：

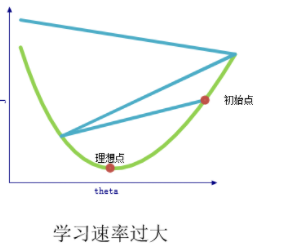
反向传播

在本次实践中，我们的函数模型为：
$$y=\frac{1}{1+e^{?(w?x+b)}}$$
网络结构图如下：

Input Layer => Layer1:
$$h=w?x+b$$

其中x为375 * 1 的矩阵，w为输入层到网络层1之间各直线的权重值，维度为9 * 375，b为偏移量，维度为9 * 1，h为网络层1的值，维度为9 * 1；

Layer1 => Output Layer9:
$$y=sigmoid(h)=\frac{1}{1+e^{?h}}$$

h为9 * 1的矩阵，那么y计算后的维度也为9 * 1。由前文sigmoid函数分析可知，y这个9 * 1的矩阵每个元素都在(0,1)之间，得到的值代表对应值的概率。可以让y1,y2,y3……y9分别代表1,2,3……9。假设max(y)=y3,那么最后该图片的预测值就为3。

计算图

计算图表示如下：

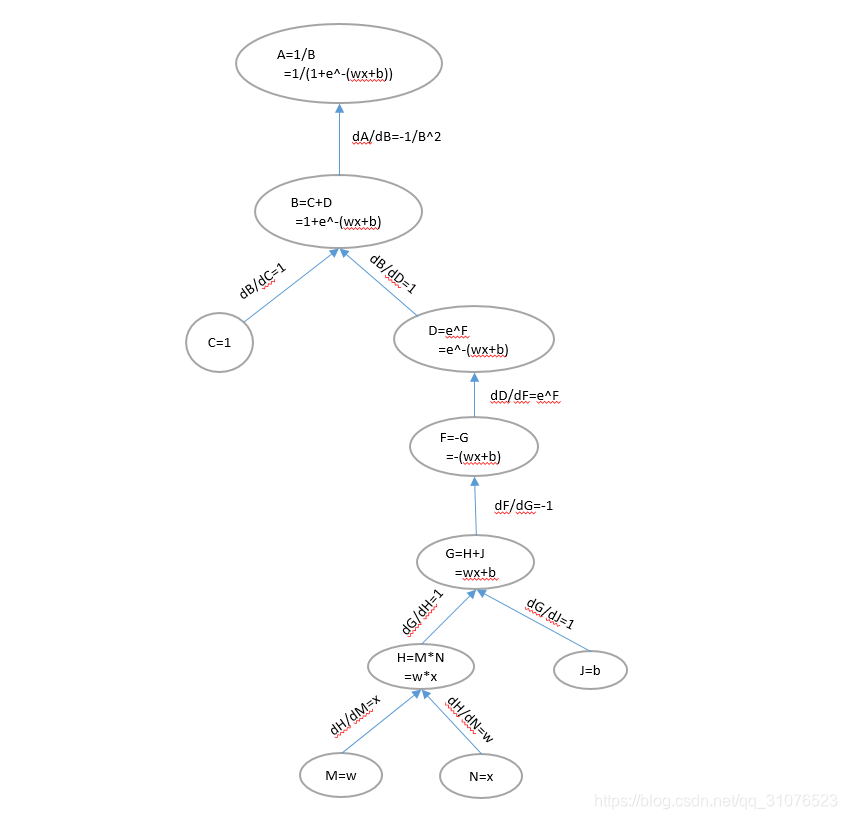
将 sigmoid 视为一个整体

求sigmoid函数的导数$y^{\prime }$：
$$y=\frac{1}{1+e^{?x}}$$
$y^{\prime }=\frac{?1}{(1+e^{?x}{)}^2}?(1+e^{?x}{)}^{\prime }$
$=\frac{?1}{(1+e^{?x}{)}^2}?e^{?x}?(?x{)}^{\prime }$
$=\frac{?1}{(1+e^{?x}{)}^2}?e^{?x}??1$
$=\frac{e^{?x}}{(1+e^{?x}{)}^2}=\frac{e^{?x}}{1+e^{?x}}?\frac{1}{1+e^{?x}}$
$=(1?\frac{1}{1+e^{?x}})?\frac{1}{(1+e^{?x})}$
$=(1?sigmod(x))?sigmoid(x)$
上述计算图中:
$$\frac{dA}{dG}=y^{\prime }$$
$dw=\frac{dA}{dM}=\frac{dA}{dG}?\frac{dG}{dH}?\frac{dH}{dM}=y^{\prime }?1?x=y^{\prime }?x$
$dx=\frac{dA}{dN}=\frac{dA}{dG}?\frac{dG}{dH}?\frac{dH}{dN}=y^{\prime }?1?w=y^{\prime }?w$
$db=\frac{dA}{dJ}=\frac{dA}{dG}?\frac{dG}{dJ}=y^{\prime }?1=y^{\prime }$

实践

数据收集

想要识别验证码，需先收集验证码图片数据。
如图，我们系统的验证码是base64格式的。

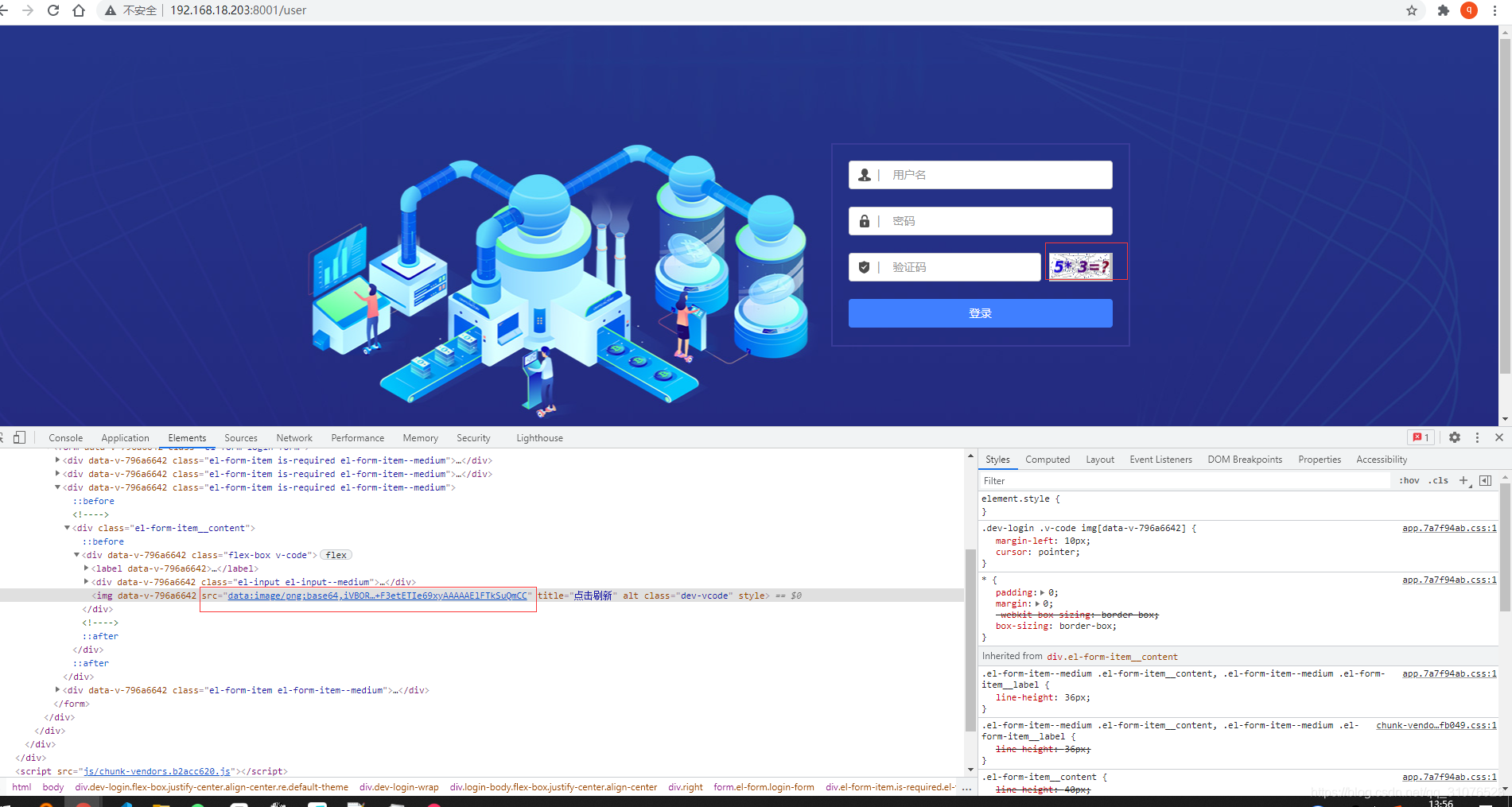
codeAutoCal\code.py

import requests,base64
import os
class Code:
    def __init__(self) -> None:
        pass

    def getCodes(self,n):
        for i in range(n):
            r=requests.get("http://192.168.18.203:8001/api/v1/common/getCapcha")
            base64Str=r.json()['data']['captcha'][22:]
            imgdata=base64.b64decode(base64Str)
            fileName=os.path.join(os.path.dirname(__file__),'sourceImg','code{}.png'.format(i+1))
            file=open(fileName,'wb')
            file.write(imgdata)
        file.close()

if __name__=='__main__':
    code=Code()
    code.getCodes(300)

上述代码，将base64字符串转为图片，保存到sourceImg目录下。共保存300张，如图：

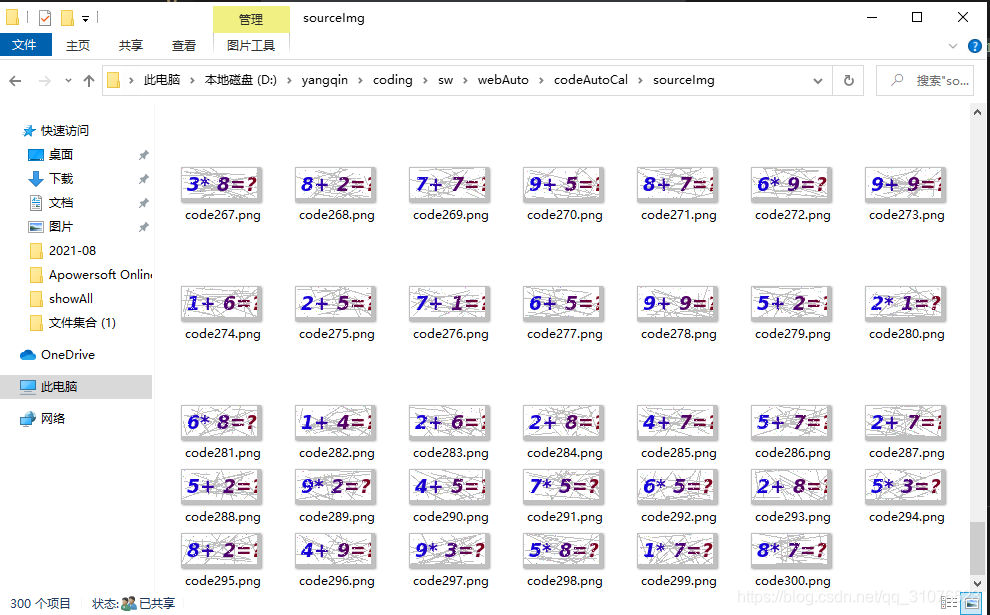
数据降噪&切割

我们的图片数据只有数字，以及加法乘法两种运算符。识别时需要将数字及运算符分开识别。并且图片含有一定噪点。所以需要降噪处理，并且将图片切割为数字以及运算符。
codeAutoCal\img_pre_deal.py

# coding:utf-8
import os
from os import path
from PIL import Image, ImageDraw

class ImagePre:
	
    def __init__(self,src,dst) -> None:
        self.src=src
        self.dst=dst
        self.t2val={}
    
    def twoValue(self,image,G):
        for y in range(0, image.size[1]):
            for x in range(0, image.size[0]):
                g = image.getpixel((x, y))
                if g > G:
                    self.t2val[(x, y)] = 1
                else:
                    self.t2val[(x, y)] = 0

    def findFirstPix(self,image):
        result=[]
        for y in range(0, image.size[1]):
            for x in range(0, image.size[0]):
                g = image.getpixel((x, y))
                if g < 255:
                    result.append(x)
                    break
        return min(result)

    def clearNoise(self,image,N,Z):
        # 根据一个点A的RGB值，与周围的8个点的RBG值比较，设定一个值N（0 <N <8），当A的RGB值与周围8个点的RGB相等数小于N时，此点为噪点
        # G: Integer 图像二值化阀值
        # N: Integer 降噪率 0 <N <8
        # Z: Integer 降噪次数
        # 输出
        #  0：降噪成功
        #  1：降噪失败

        for i in range(0, Z):
            self.t2val[(0, 0)] = 1
            self.t2val[(image.size[0] - 1, image.size[1] - 1)] = 1

            for x in range(1, image.size[0] - 1):
                for y in range(1, image.size[1] - 1):
                    nearDots = 0
                    L = self.t2val[(x, y)]
                    if L == self.t2val[(x - 1, y - 1)]:
                        nearDots += 1
                    if L == self.t2val[(x - 1, y)]:
                        nearDots += 1
                    if L == self.t2val[(x - 1, y + 1)]:
                        nearDots += 1
                    if L == self.t2val[(x, y - 1)]:
                        nearDots += 1
                    if L == self.t2val[(x, y + 1)]:
                        nearDots += 1
                    if L == self.t2val[(x + 1, y - 1)]:
                        nearDots += 1
                    if L == self.t2val[(x + 1, y)]:
                        nearDots += 1
                    if L == self.t2val[(x + 1, y + 1)]:
                        nearDots += 1

                    if nearDots < N:
                        self.t2val[(x, y)] = 1

    def split_img(self,image,index):
    	# 存储操作数图片的路径
        picDir=path.join(path.dirname(image),'..','pic')
		# 存储符号图片的路径
        symboldir=path.join(path.dirname(image),'..','picSymbol')

        
        image1 = Image.open(image).crop((5, 5, 20, 30))
        image1.save(path.join(picDir,str(index)+'.png'))
		
		# 得到操作数的图片，尺寸为10*25
        image2 = Image.open(image).crop((20, 5, 30, 30))
        image2.save(path.join(symboldir,str(index//2)+'.png'))
        
        # 因为加号和乘号视觉宽度不相等，所以第二个操作数切割位置不一样。根据图片中的第一个像素点位置确定切割起始位置。crop(35, 5, 50, 30)代表横坐标取35~50。纵坐标取5~30.最终切割后的图片大小为15*25
        image3 = Image.open(image).crop((35, 5, 50, 30))
        if(self.findFirstPix(image3)>2):
            image3=Image.open(image).crop((41, 5, 56, 30))        

        image3.save(path.join(picDir,str(index+1)+'.png'))

    def saveImage(self,filename,size):
        image = Image.new("1", size)
        draw = ImageDraw.Draw(image)

        for x in range(0, size[0]):
            for y in range(0, size[1]):
                draw.point((x, y), self.t2val[(x, y)])

        image.save(filename)
        

    def main(self):
        list=os.listdir(self.src)
        for i,f in enumerate(list):
            source=os.path.join(self.src,f)
            target=os.path.join(self.dst,f)
            # 彩色变黑白
            image=Image.open(source).convert('L')
            # 在色度中，255是白色，0是黑色，此方法将灰度大于100的变为白色，将灰度小于100的变为黑色
            self.twoValue(image,100)
            #降噪处理，判断噪点并将噪点变为白色
            self.clearNoise(image,2,1)
            self.saveImage(target,image.size)
            # 将图片切割为数字以及运算符
            self.split_img(target,2*i)


if __name__=='__main__':
    targetPath = r'D:\yangqin\coding\sw\webAuto\codeAutoCal\noiseImg'
    originPath=r'D:\yangqin\coding\sw\webAuto\codeAutoCal\sourceImg'
    imgpre=ImagePre(originPath,targetPath)
    imgpre.main()

上述代码将sourceImg中的原始图片，得到降噪处理后的图片。再把降噪处理后的图片（目录：noiseImg）切割为操作数图片（目录：pic，尺寸：15 * 25）、运算符图片（目录：picSymbol，尺寸：10 * 25）。如下：
降噪后图片：

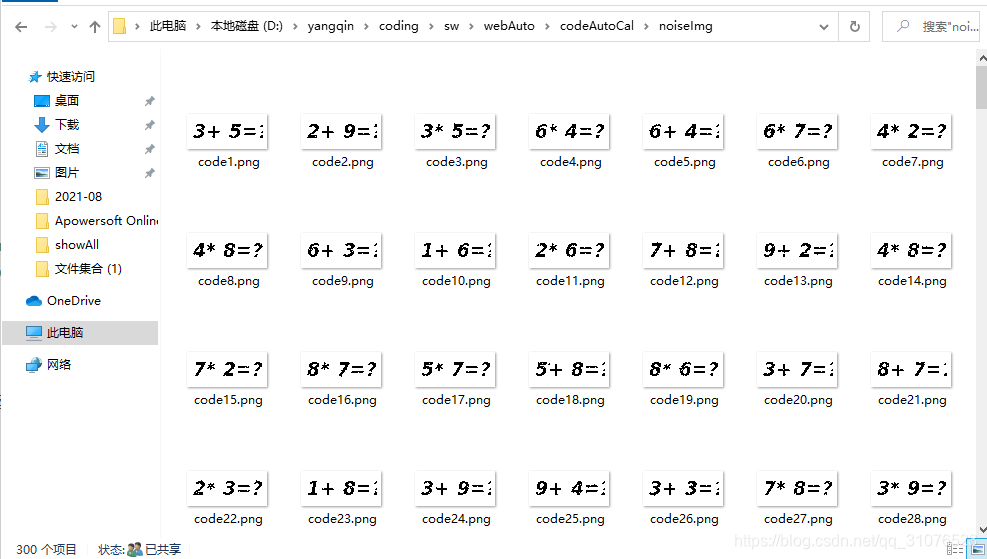
操作数图片：

运算符图片：

数据标记

上述图片共计300张，拆分后运算符300张，操作数600张。本文以识别操作数为例（运算符逻辑相同，并且更加简单，因为运算符只有加法乘法两种结果，而操作数有1~9共9种结果），是的，我们项目的验证码数字不会出现0。
通常需要将样本数据划分为三个部分：train.txt、validate.txt、test.txt

train.txt、validate.txt和test.txt将我们的数据划分成了三个部分。进行这样的划分是有原因的，在实际运用深度学习解决分类问题的过程中，我们总是将数据划分为训练集、验证集和测试集。
我们的学习算法learn利用训练集来对模型中的参数进行优化，为了检验这些参数是否足够 “好”，可以通过观察训练过程中的损失函数值来判断，但通过损失函数值来判断有一个问题，就是我们的模型可能只是“记住” 了所有的训练数据，而不是真正的学会了训练数据中所包含的问题本身的性质。就像是如果我们考试时总是出原题，那笨学生只要把所有题目都记住也一样可以取得高分。
所以为了检验我们的模型是在 “学习” 而不是在“死记硬背”，我们再使用与训练集不同的验证集对模型进行测试，当模型对验证集的分类准确率也比较高时，就可以认为我们的模型是真正的在 “学习”，此时我们称我们的模型拥有较好的泛化性能（generalization）-- 能够正确的对未曾见过的测试样例做出正确的预测。
然而这里还是有一个问题，别忘了除了模型里的参数，我们还手动设置了超参数，我们的超参数也有可能只能适应一部分数据，所以为了避免这种情况，需要再设置一个与训练集和验证集都不同的测试集，测试在当前超参数的设置下，我们的模型具有良好的泛化性能。

以上为教程原内容，本次实践简化处理，只用将前400条数据划分为train.txt，用于训练；后200条数据划分为validate.txt，用于验证准确度。
如下，train.txt用于训练数据，标记编号为0~399的图片，共400张。

同样的方法编写validate.txt用于预测数据，标记400~599的图片，共计200张。

数据预处理

前文中，我们已经得到了图片样本数据（15*25）。对于图片数据，需要将他们转为输入向量形式。图片预处理程序如下：
codeAutoCal\pretreatment.py

import imageio
import numpy as np

import os
class Img2Array:
    def __init__(self) -> None:
        pass
    def main(self,src,dst):        
        with open(src, 'r') as f:  # 读取图片列表
            list = f.readlines()
        data = []
        labels = []
        base=os.path.dirname(__file__)
        for i in list:
            name, label = i.strip('\n').split(' ')  # 将图片列表中的每一行拆分成图片名和图片标签
            print(name + ' processed')
            name=os.path.join(base,name)
            img = imageio.imread(name) # 将图片读取出来，存入一个矩阵
            img = img/255 # 将图片转换为只有0、1值的矩阵，前面降噪时，已经二值化过了，原始数据本来就只有0/1,此步骤非必须，但为了通用起见，还是写了这一步
            img.resize((img.size, 1))  # 为了之后的运算方便，我们将图片存储到一个img.size*1的列向量里面。次数img.size为15*25
            data.append(img)
            labels.append(int(label))

        print('write to npy')
        np.save(dst, [data, labels])  # 将训练数据以npy的形式保存到成本地文件
        print('completed')

if __name__=='__main__':
    img=Img2Array()
    base=os.path.join(os.path.dirname(__file__),'data')
    img.main(os.path.join(base,'train.txt'),os.path.join(base,'train.npy'))
    img.main(os.path.join(base,'validate.txt'),os.path.join(base,'validate.npy'))

编写数据层

数据层即读取预处理后train.npy，validate.npy的数据。batch_size指定一次性读取数据的数量。forward方法可以读取下一组数据。数据训练时，需要训练多个周期，通过不断减少代价函数的损失值，缩小误差。所以在每个周期（epoch）读取数据时，可以将训练数据打乱（np.random.shuffle），从而得到更好的训练效果。
codeAutoCal\data.py

import numpy as np

class Data:
    def __init__(self, name, batch_size):  # 数据所在的文件名name和batch中图片的数量batch_size
        with open(name, 'rb') as f:
            data = np.load(f, allow_pickle=True)
        self.x = data[0]  # 输入x
        self.y = data[1]  # 预期正确输出y
        self.l = len(self.x)
        self.batch_size = batch_size
        self.pos = 0  # pos用来记录数据读取的位置

    def forward(self):
        pos = self.pos  
        bat = self.batch_size
        l = self.l
        if pos + bat >= l:  # 已经是最后一个batch时，返回剩余的数据，并设置pos为开始位置0
            ret = (self.x[pos:l], self.y[pos:l])
            self.pos = 0
            index = np.array(range(l))
            np.random.shuffle(index)  # 将训练数据打乱
            self.x = self.x[index]
            self.y = self.y[index]
        else:  # 不是最后一个batch, pos直接加上batch_size
            ret = (self.x[pos:pos + bat], self.y[pos:pos + bat])
            self.pos += self.batch_size

        return ret, self.pos  # 返回的pos为0时代表一个epoch已经结束

    def backward(self, d):  # 数据层无backward操作
        pass

编写模型层

编写全连接层

注意在神经网络中，我们将层与层之间的每个点都有连接的层叫做全连接（fully connect）层，所以我们将这里的类命名为FullyConnect

codeAutoCal\fullyConnect.py

import numpy as np
# y=sigmoid(wx+b)
class FullyConnect:
    def __init__(self,l_x,l_y) -> None:
        self.weights=np.random.randn(l_y,l_x)/np.sqrt(l_x)
        self.bias=np.random.randn(l_y,1)
        self.l_r=0
        
    def forward(self,x):
        self.x=x
        self.y=np.array([self.weights.dot(xx)+self.bias for xx in x])
        return self.y

	# 参数d为sigmoid传回来的损失函数的导数,其维度为50*9*1，50代表data.batchSize
    def backward(self,d):
        ddw=[dd.dot(xx.T) for xx,dd in zip(self.x,d)]
        self.dw=np.sum(ddw,axis=0)/self.x.shape[0]
        self.db=np.sum(d,axis=0)/self.x.shape[0]
        self.dx=np.array([self.weights.T.dot(dd) for dd in d])
        
        self.weights-=self.l_r*self.dw
        self.bias-=self.l_r*self.db
        return self.dx

为了理解上面的代码，我们以一个包含 50个训练输入数据的 batch 为例，分析一下具体执行流程： 我们的 l_x 为输入单个数据向量的长度，在这里是 15 * 25=375，l_y 代表全连接层输出的节点数量，由于本案例中数字的可能只有1-9，共9个，所以这里的 l_y=9。 所以，我们的 self.weights 的尺寸为 9 * 375, self.bias 的尺寸为 9 * 1（self.bias 也是通过矩阵形式表示的向量）。forward() 函数的输入 x 在这里的尺寸就是 50 * 375 * 1(batch_size * 向量长度 * 1)。backward() 函数的输入 d 代表从前面的网络层反向传递回来的 “部分梯度值”，其尺寸为 50 * 9 * 1（batch_size * 输出层节点数 l_y * 1）。

1. forward() 函数里的代码比较好理解，由于这里的 x 包含了多组数据，所以要对每组数据分别进行计算。
2. backward() 函数的理解参考前文的反向传播，各数据维度如下：
   ddw维度为：50 *9 * 375
   dw维度为： 9 * 375
   db维度为： 9 * 1
   dx维度为： 375 * 1
3. self.lr 即为前面我们提到过的学习速率alpha，也被称为超参数。

编写sigmoid层代码

codeAutoCal\sigmoid.py

import numpy as np
class Sigmoid:
    def __init__(self):  # 无参数，不需初始化
        pass

    def sigmoid(self, x):
        return 1 / (1 + np.exp(-x))

    def forward(self, x):
        self.x = x
        self.y = self.sigmoid(x)
        return self.y

    def backward(self, d):
        sig = self.sigmoid(self.x)
        self.dx = d * sig * (1 - sig)
        return self.dx  # 反向传递梯度

backward即求sigmoid导数，参考前文的反向传播

编写损失层代码

codeAutoCal\crossEntropyLoss.py

import numpy as np
class CrossEntropyLoss:
    def __init__(self):
        pass

    def forward(self, x, label):
        self.x = x
        self.label = np.zeros_like(x)
        for a, b in zip(self.label, label):
            a[b-1] = 1.0
        # np.nan_to_num()避免log(0)得到负无穷的情况
        self.loss = np.nan_to_num(-self.label *
                                  np.log(x) - ((1 - self.label) * np.log(1 - x)))
        self.loss = np.sum(self.loss) / x.shape[0]
        return self.loss

    def backward(self):
        self.dx = (self.x - self.label) / self.x / \
            (1 - self.x)  # 分母会与Sigmoid层中的对应部分抵消
        return self.dx

本节理解参考前文的损失函数>交叉熵函数。x为预测值，维度为50 * 9 * 1。label为[1,9]中的某一个值，会转化为self.label，维度为50 * 9 * 1。不考虑batchSize的情况，对单个label来说，转换关系如下，当label为3时，self.label为[0,0,1,0,0,0,0,0,0]。即只有序号为2也就是第3个元素为1，其他元素全为0

准确度计算

codeAutoCal\accuracy.py

import numpy as np
class Accuracy:
    def __init__(self) -> None:
        pass

    def forward(self,x,label):
        self.accuracy= np.sum([np.argmax(xx)==ll-1 for xx,ll in zip(x,label)])
        self.accuracy=1.0*self.accuracy/x.shape[0]
        return self.accuracy

x为预测值，label为实际值，x和label维度为50 * 9 * 1，那么xx和LL维度为9 * 1，xx中最大值的序号如果等于LL-1，即代表预测正确。使用预测正确的个数/总个数即为该批数据的预测的准确度。

训练模型

codeAutoCal\test_main.py

from data import Data
from fullyConnect import FullyConnect
from quadraticLoss import QuadraticLoss
from crossEntropyLoss import CrossEntropyLoss
from sigmoid import Sigmoid
from accuracy import Accuracy
import numpy as np
from os import path

base=path.join(path.dirname(__file__),'data')
def main():
    datalayer1=Data(path.join(base,'train.npy'),50)
    datalayer2=Data(path.join(base,'validate.npy'),50)
   
    inner_layers=[]
    inner_layers.append(FullyConnect(15*25,4)) # 10*25
    inner_layers.append(Sigmoid())
    inner_layers.append(FullyConnect(4,9))
    inner_layers.append(Sigmoid())
    losslayer=CrossEntropyLoss()
    accuracy=Accuracy()

    EPOCHS=600
    for layer in inner_layers:
        layer.l_r=0.06
    
    for i in range(EPOCHS):
        print('epochs:',i)
        lossum=0
        iter=0
        while True:
            data,pos=datalayer1.forward()
            x,label=data
            for layer in inner_layers:
                x=layer.forward(x)

            loss=losslayer.forward(x,label)
            lossum+=loss
            iter+=1            
            d=losslayer.backward()
            for layer in inner_layers[::-1]:
                d=layer.backward(d)
            if pos==0:
                data,_=datalayer2.forward()
                x,label=data
                for layer in inner_layers:
                    x=layer.forward(x)
                accu=accuracy.forward(x,label)
                print('loss:',lossum/iter)
                print('accuracy:',accu)
                break
    return inner_layers


if __name__ == '__main__':
    # 训练，保存模型
    models=main()
    # np.savetxt(r'D:\yangqin\coding\sw\webAuto\codeAutoCal\args\args1_w.txt',models[0].weights, fmt="%f", delimiter=" ")
    # np.savetxt(r'D:\yangqin\coding\sw\webAuto\codeAutoCal\args\args1_b.txt',models[0].bias, fmt="%f", delimiter=" ")
    # np.savetxt(r'D:\yangqin\coding\sw\webAuto\codeAutoCal\args\args2_w.txt',models[2].weights, fmt="%f", delimiter=" ")
    # np.savetxt(r'D:\yangqin\coding\sw\webAuto\codeAutoCal\args\args2_b.txt',models[2].bias, fmt="%f", delimiter=" ")

上述代码增加了一层网络层，从浅层变成了深层。从而使精确度更高，至于原因，比较抽象，请参考教程，如下图所述。

深度神经网络可以利用 “层次化” 的信息表达减少网络中的参数数量，而且能够提高模型的表达能力，即靠后的网络层可以利用靠前的网络层中提取的较低层次的信息组合成更高层次或者更加抽象的信息。

在训练模型的main方法中，我们通过调整周期EPOCHS和学习速率l_r，可以得到一个准确率较高的model，如果得到了一个满意的模型，可以通过main方法中注释的save方法，将模型参数w和b持久化存储，从而在预测值的时候可以直接使用模型参数，而不是每次预测都去训练模型。

预测值

codeAutoCal\predict .py

from pretreatment import Img2Array
import numpy as np
from fullyConnect import FullyConnect
from sigmoid import Sigmoid
from data import Data
from img_pre_deal import ImagePre
import sys,os
sys.path.append(os.path.dirname(__file__))
class Predict:
	# imgPath为输入待预测的验证码图片路径
    def __init__(self,imgPath) -> None:
        self.inner_layers=[]
        self.inner_layers_symbol=[]
        self.f1=FullyConnect(15*25,4) 
        self.f2=FullyConnect(4,9) #f1和f2使用两层网络层来预测操作数1~9
        self.f3=FullyConnect(10*25,2) # 预测运算符是加号或乘号，方法和预测操作数类似，本文未介绍相关内容
        self.base=os.path.dirname(__file__)
        self.imgPath=imgPath
        self.initLayer()

    def initLayer(self):
    	# 初始化网络层，读取f1和f2的模型参数值，用以预测操作数
        self.inner_layers.append(self.f1)
        self.inner_layers.append(Sigmoid())
        self.inner_layers.append(self.f2)
        self.inner_layers.append(Sigmoid())      
        args1_w=np.array(np.loadtxt(os.path.join(self.base,'args','args1_w.txt')))
        args1_b=np.array(np.loadtxt(os.path.join(self.base,'args','args1_b.txt')))
        args2_w=np.array(np.loadtxt(os.path.join(self.base,'args','args2_w.txt')))
        args2_b=np.array(np.loadtxt(os.path.join(self.base,'args','args2_b.txt')))
        args1_b=args1_b.reshape((args1_b.size,1))
        args2_b=args2_b.reshape((args2_b.size,1))
        self.f1.weights,self.f1.bias=(args1_w,args1_b)
        self.f2.weights,self.f2.bias=(args2_w,args2_b)
		
		# 初始化网络层，读取f3的模型参数值，用以预测运算符
        self.inner_layers_symbol.append(self.f3)
        self.inner_layers_symbol.append(Sigmoid())
        args3_w=np.array(np.loadtxt(os.path.join(self.base,'args','args3_w.txt')))
        args3_b=np.array(np.loadtxt(os.path.join(self.base,'args','args3_b.txt')))
        args3_b=args3_b.reshape((args3_b.size,1))
        self.f3.weights,self.f3.bias=(args3_w,args3_b)
	# 将原始图片降噪，切割成操作数和运算符两类，放置到tmp目录下
    def preDeal(self):
        originDir=os.path.dirname(self.imgPath)
        targetDir=os.path.join(self.base,'tmp','noiseImg') 
        self.del_file(os.path.join(self.base,'tmp'))
        imgpre=ImagePre(originDir,targetDir)
        imgpre.main()
    # 每次识别时，删除tmp下的文件
    def del_file(self,path):
        ls = os.listdir(path)
        for i in ls:
            c_path = os.path.join(path, i)
            if os.path.isdir(c_path):
                self.del_file(c_path)
            else:
                os.remove(c_path)
    # 对输入的图片转为数组，并利用已有模型预测操作数，因为每个验证码有两个操作数，所以此函数返回的值为元组，分别代表两个预测数
    def preDict(self):
        img=Img2Array()
        img.main(os.path.join(self.base,'data','predict.txt'),os.path.join(self.base,'data','predict.npy'))
        datalayer=Data(os.path.join(self.base,'data','predict.npy'),2)        
        data,_=datalayer.forward()
        x=data[0]
        for layer in self.inner_layers:
            x=layer.forward(x)
        r=np.argmax(x,axis=1)+1
        return r[0][0],r[1][0]


	 # 预测运算符，逻辑一致，不赘述
    def preDictSymbol(self):
        img=Img2Array()
        img.main(os.path.join(self.base,'data','predictSymbol.txt'),os.path.join(self.base,'data','predictSymbol.npy'))
        datalayer=Data(os.path.join(self.base,'data','predictSymbol.npy'),2)        
        data,_=datalayer.forward()
        x=data[0]
        for layer in self.inner_layers_symbol:
            x=layer.forward(x)
        symbols=['+','*']
        index=np.argmax(x,axis=1)[0][0]
        return (symbols[int(index)],)
# 主方法，返回三个元素的元组，前两个为操作数，最后一个为运算符
    def main(self):
        self.preDeal()
        r1=self.preDict()
        return r1+self.preDictSymbol()


if __name__ == '__main__':
    # 测试方法
    imgPath=r'D:\yangqin\coding\sw\webAuto\screenCapture\code\code.png'
    p=Predict(imgPath)
    r=p.main()
    print(r)

最终代码调用

util/get_code.py

from PIL import Image,ImageDraw
import os
from os import path

from selenium.webdriver.remote.switch_to import SwitchTo
from codeAutoCal.predict import Predict
class GetCode(object):
    def __init__(self,driver):
        self.driver=driver
        
    def save_code_img(self,code_el,saveName):
        self.driver.save_screenshot(saveName)
        left = code_el.location['x']
        top = code_el.location['y']
        right = left+code_el.size['width']
        bottom = top+code_el.size['height']
        image = Image.open(saveName).crop((left, top, right, bottom))
        image.save(saveName)
    
    def getCode(self,imgPath):
        p=Predict(imgPath)
        r=p.main()
        symbol=r[2]
        c1=int(r[0])
        c2=int(r[1])
        result=0
        if symbol=='+':
            result=c1+c2
        elif symbol=='*':
            result=c1*c2
        return result

if __name__=='__main__':
    pass

handle/login_handle.py

    # 输入验证码
    def send_code(self,code=None):
        if code:
            self.login_p.get_code_element().send_keys(code) 
        else:
            codeImgEl=self.login_p.get_code_img_element() # 获取验证码元素
            codeUtil=GetCode(self.driver) # 实例化GetCode对象
            codePath=os.path.join(os.getcwd(),'screenCapture','code','code.png')
            codeUtil.save_code_img(codeImgEl,codePath) # 保存验证码截图
            code=codeUtil.getCode(codePath) # 识别验证码图片结果
            self.login_p.get_code_element().send_keys(code)   

当code传值时，直接发送指定值，当code不传时，则使用我们训练好的模型，来计算code的值。

文末

本来打算简单总结下本次实践，没想到洋洋洒洒写了这么多，(⊙﹏⊙)。那就给个github链接吧，深度学习实现验证码识别的所有代码都在codeAutoCal目录下。
完整项目github连接